МОДЕЛИРОВАНИЕ РИСКОВ НА РЫНКЕ ЦЕННЫХ БУМАГ

Финансовый риск

Профессия финансиста столь же рискованна, как и профессия подводника, летчика или космонавта. Всякая финансовая операция связана с возможным либо обогащением, либо разорением. Введем понятие финансового риска и построим его количественные характеристики.

Финансовая операция (сделка) называется рискованной, если ее эффективность недетерминирована, т. е. не известна в момент заключения сделки.

В этом случае эффективность финансовой сделки является случайной величиной и зависит от случайных обстоятельств.

Другими словами рискованную финансовую сделку нельзя характеризовать каким-либо одним значением эффективности.

Рискованной сделке соответствует целый ансамбль возможных значений эффективности, реализующихся с той или иной вероятностью.

Если удается получить некоторые вероятностные характеристики эффективности сделки, то может быть поставлена задача ограничения или минимизации риска при заданном уровне доходности сделки.

Практически любая финансовая сделка является рискованной, лишь некоторые финансовые операции с некоторой степенью условности можно считать безрисковыми. Например, государственные процентные бумаги экономически развитых стран.

Построим некоторые количественные характеристики риска. Чтобы разговор не был слишком абстрактным, рассмотрим финансовые операции с акциями, эффективность которых может характеризоваться величиной:

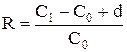, (5.1)

где

С₀ – цена покупки акции в момент 0;

С₁ – цена продажи в момент 1;

d – дивиденды, полученные за время от начального момента 0 до конечного момента 1.

Заметим, что аналогичный критерий эффективности может быть построен для других ценных бумаг, например, для облигаций. Тогда, С₀ – цена покупки облигации, С₁ – цена продажи облигации, d – доход от купонов.

Эффективность R, как уже отмечалось выше, является случайной величиной. Самой полной информацией о случайной величине была бы плотность функции распределения этой величины. Для дальнейших исследований достаточно более скромной информации о случайной величине. Будем считать, что известны некоторые вероятностные характеристики (например, из анализа прошлого фондового рынка), позволяющие построить математическое ожидание m эффективности:

m=E(R), (5.2)

где E( ) обозначает математическое ожидание, т. е. осреднение по всему ансамблю возможных значений.

Степень отклонения случайной эффективности R от ее математического ожидания m характеризуется дисперсией (вариацией), равной:

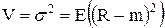, (5.3)

где

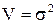– вариация или дисперсия;

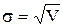– среднеквадратическое отклонение.

Дисперсия или вариация всегда больше нуля. Размерность математического ожидания совпадает с размерностью случайной величины. Размерность дисперсии случайной величины равна квадрату размерность самой случайной величины. Размерность среднеквадратического отклонения случайной величины совпадает с размерностью случайной величины.

Величина дисперсии (вариации) является количественной оценкой степени рискованности сделки, чем больше дисперсия, тем более рискованной является финансовая сделка. В предельном случае для безрисковых операций дисперсия равна нулю.