Расчет Н нормы рентабельности (индекса доходности) инвестиционного проекта
| процентная ставка r= | 10,00% | ||||
| Даты | Значения (млн. руб.) | инвестиции C- | доходы C+ | дисконт. сумма доходов | Н |
| 01.01.2008 | -100 | 100,0 | |||
| 01.01.2009 | -150 | 150,0 | |||
| 01.01.2010 | 0,00 | 0,000 | |||
| 01.01.2011 | 45,07 | 0,191 | |||
| 01.01.2012 | 86,04 | 0,364 | |||
| 01.01.2013 | 123,27 | 0,522 | |||
| 01.01.2014 | 157,12 | 0,665 | |||
| 01.01.2015 | 187,90 | 0,795 | |||
| 01.01.2016 | 215,87 | 0,913 | |||
| 01.01.2017 | 241,30 | 1,021 | |||
| 01.01.2018 | 264,41 | 1,119 | |||
| 01.01.2019 | 285,43 | 1,208 | |||
| 01.01.2020 | 304,53 | 1,289 |
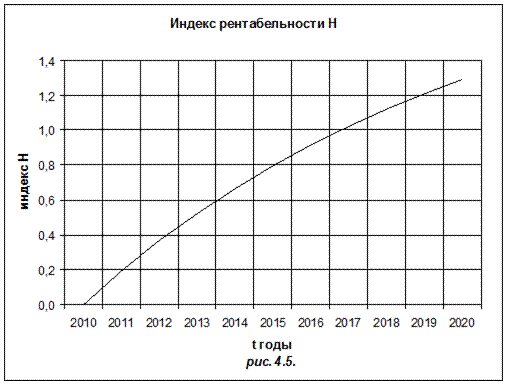
На рис 4.5 и в шестом столбце таблицы представлена зависимость нормы рентабельности H(t) от времени t при процентной ставке r=10 %. В момент времени 01.01.2017 она составляет Н=1,021. Это значение превышает единицу то, есть на 1 руб. инвестиций получено 1,021 руб. дохода, что соответствует времени окупаемости инвестиционного проекта.
Пример56. Оценка риска инвестиционного проекта.
Инвестиционный проект задан двусторонним потоком платежей. Соответствующий поток приведен в двух первых столбцах таблицы 4.3. Процентная ставка является случайной величиной, распределенной по нормальному закону с математическим ожиданием a = 10 % и среднеквадратическим отклонением σ = 3 %. Найти вероятность окупаемости инвестиционного проекта на момент времени t.
Решение.
Процентная ставка распределена по нормальному закону. Функция распределения нормально распределенной случайной величины с математическим
ожиданием a и среднеквадратическим отклонением σ имеет вид:
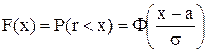 ,
,
где для расчета вероятности P(r < x) используется нормированная нормальная функцию распределения 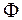 с математическим ожиданием 0 и дисперсией 1 и заданная интегралом Лапласа:
с математическим ожиданием 0 и дисперсией 1 и заданная интегралом Лапласа:
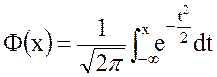 .
.
Для перехода к нормированной нормальной функции распределения центрируем случайную величину по формуле 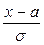 . Для вычисления функции Лапласа можно использовать таблицы или функцию НОРМСТРАСП( ) из Excel.
. Для вычисления функции Лапласа можно использовать таблицы или функцию НОРМСТРАСП( ) из Excel.
Согласно п. 4.2 чистое современное значение NPV зависит от процентной ставки r и времени t , то есть NPV = NPV(r, t ). Фиксируем время t. Если процентная ставка r является случайной величиной, то и современное значение NPV будет случайной величиной. Окупаемость проекта наступает, когда современное значение NPV становится больше нуля, т. е. окупаемости проекта соответствует событие NPV( r, t )>0. Найдем вероятность этого события:
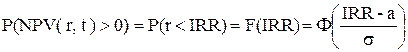 ,
,
где IRR – эффективная ставка проекта на момент t. Согласно п. 4.3 она является решением уравнения NPV(t, IRR) = 0.
Тогда, используя для вычисления интеграла Лапласа функцию НОРМСТРАСП( ) и функцию ЧИСТВНДОХ( ) для вычисления эффективной ставки IRR, найдем вероятность того, что инвестиционный проект окупится к моменту t. Результаты расчетов приведены в таблице 4.3 и проиллюстрированы рис 4.6.
Таблица 4.3.
Зависимость вероятности окупаемости от длительности проекта
| Даты | Суммы | Эффективная ставка IRR | Вероятность окупаемости |
| 01.01.2008 | -100 | ||
| 01.01.2009 | -150 | ||
| 01.01.2010 | |||
| 01.01.2011 | -45,78% | 0,000000 | |
| 01.01.2012 | -22,34% | 0,000000 | |
| 01.01.2013 | -9,15% | 0,000000 | |
| 01.01.2014 | -1,04% | 0,000117 | |
| 01.01.2015 | 4,26% | 0,027946 | |
| 01.01.2016 | 7,89% | 0,240954 | |
| 01.01.2017 | 10,46% | 0,560307 | |
| 01.01.2018 | 12,32% | 0,780335 | |
| 01.01.2019 | 13,71% | 0,891625 | |
| 01.01.2020 | 14,75% | 0,943478 | |
| 01.01.2021 | 15,56% | 0,968051 | |
| 01.01.2022 | 16,18% | 0,980370 |
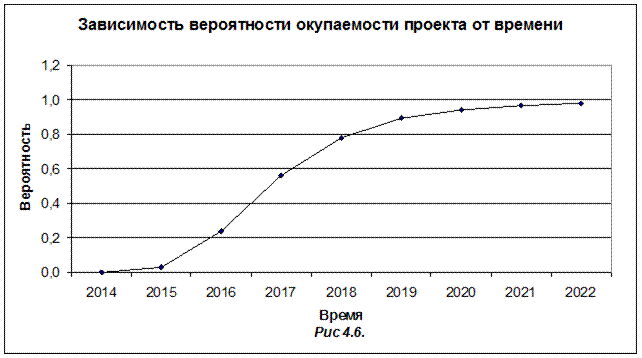
Таким образом, если процентная ставка является случайной величиной, распределенной по нормальному закону с математическим ожиданием a = 10 % и среднеквадратическим отклонением σ = 3 %, то вероятность окупаемости проекта на 2017 год равна 0,56 на 2018 и 2019 годы она возрастет и будет равна соответственно 0,78; 0,89.
Дата добавления: 2016-03-15; просмотров: 691;
