Неравенство Чебышева. Вероятность того, что случайная величина R отклонится от своего математического ожидания m больше, чем заданное значение d
Теорема Чебышева
Вероятность того, что случайная величина R отклонится от своего математического ожидания m больше, чем заданное значение d, не превосходит ее дисперсии s2, деленной на d2, т. е.:
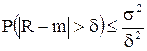, (5.4)
где Р(*) обозначает вероятность события *.
Воспользоваться теоремой Чебышева для решения следующей задачи.
Задача 40.
Господин А делает заем под процент r и под залог недвижимости. На полученные взаймы деньги господин А покупает акции. Пусть эффективность R покупаемых господином А акций характеризуется математическим ожиданием дохода m и дисперсией s2, оценивающей рискованность финансовой операции. Найти соотношение между r, m, s, при которой вероятность того, что господин А не сможет вернуть долг и лишится недвижимости меньше или равна 0,04.
Хеджирование
Для иллюстрации хеджирования рассмотрим следующий модельный пример.
Инвестор-кредитор А собирается вложить сумму С в дело под r процентов. Ожидаемый доход равен R=Cr. Однако операция инвестору представляется рискованной, и он решает приобрести страховой полис, гарантирующий выплату определенной суммы в случае провала сделки.
Для этого сумму С инвестор разделяет на две части: Cx он вкладывает в сделку и, C(1-x) он тратит на страховку, где х, 1-х – доля суммы, потраченная на финансовую сделку и страховой полис соответственно. Возможны два варианта развития событий.
Вариант 1.
Сделка оказалась удачной. В результате получен доход:
.
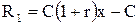Вариант 2.
Сделка не удалась. Инвестор получает страховую выплату в размере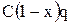 
, где q – отношение страхового возмещения к цене полиса. Тогда полученный доход равен:
.
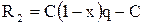Очевидно, логично выбрать х так, чтобы доход в обоих случаях был одинаков R1=R2. Решив линейное уравнение, получим:
.
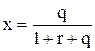При этом доход будет равен:
.
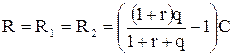Таким образом, данная схема хеджирования исключает неопределенность, при этом эффективность сделки снижается с r до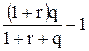 
.
Задача 41.
Рассмотреть численный пример хеджирования. Пусть r=0,1, а q=40. Найти долю средств, отпускаемых на сделку и долю средств на страховку. Определить эффективность хеджирования.
Занятие № 6. Тема «портфель ценных бумаг».
«построение оптимального портфеля ценных бумаг при рискованных вложениях»
Задача 42.
 |
Осторожный инвестор формирует портфель из 3-х ценных бумаг. Средняя эффективность портфеля из 3-х ценных бумаг равна:
где xk – доля средств затраченных на k- ую ценную бумагу.
Риск сделки, определенный как дисперсия ее эффективности, равен:
 |
При этом предполагается, что выполнено условие баланса:
x1 + x2 + x3 = 1
Найти структуру портфеля ценных бумаг, обеспечивающую минимальный риск. Найти соответствующий минимальный риск и соответствующую среднюю эффективность оптимального портфеля. Сравнить доходность и риск оптимального портфеля ценных бумаг со случаями:
‑ вложения всех средств в наиболее доходную;
‑ в наименее рискованную ценную бумагу;
‑ со случаем вложения всех средств равными порциями во все ценные бумаги.
Задача 43.
Инвестор формирует портфель из 4-х ценных бумаг, одна из которых является государственной безрисковой бумагой. Средняя эффективность портфеля из 4-х ценных бумаг равна:
 |
где xk – доля средств затраченных на k- ую ценную бумагу, в частности x0 средств затрачено на безрисковую ценную бумагу.
Риск сделки, определенный как дисперсия эффективности, равен:
 |
При этом предполагается, что выполнено условие баланса:
Найти структуру портфеля ценных бумаг, обеспечивающую минимальный риск при фиксированной доходности. Найти соответствующий минимальный риск.
Дата добавления: 2016-03-15; просмотров: 1147;