Линейная регрессия. Парная линейная регрессия

Пусть имеются две случайные величины X и Y. Можно ли считать их линейно связанными, т. е. можно ли Y считать линейной функцией от X? Каковы коэффициенты в этой линейной функции?

Сначала будем считать, что математические ожидания x и y равны нулю, ◦т. е.:

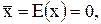
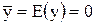(П.14)

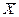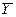Это не очень большое ограничение, так как в случае отличия от нуля математических ожиданий и , всегда можно перейти к центрированным случайным величинам 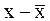, 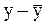. Для них математическое ожидание будет равно нулю.

Найдем коэффициент m, обеспечивающий наилучшую линейную связь между y и x:

y = mּx (П.15)

Коэффициент m можно выбрать так, чтобы дисперсия разности (невязки)

(П.16)

была минимальной.

Таким образом, m выбирается из минимума функции

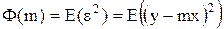(П.17)

Задача нахождения m, обеспечивающего min функции (П.17), типичной задачей метода наименьших квадратов. Для её решения распишем функцию (П.17)

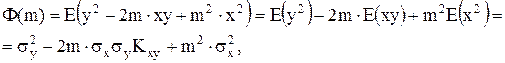
где 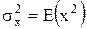- дисперсия x,

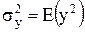- дисперсия y,

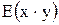- ковариация x и y,

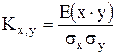- коэффициент корреляции между x и y.

Коротко имеем:

(П.18)

Для нахождения m минимизирующего функцию Φ(m) приравняем к нулю производную:

отсюда 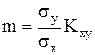(П.19)

Таким образом, уравнение линейной регрессии для случайных величин с нулевым математическим ожиданием имеет вид:

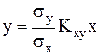(П.20)

В общем случае при замене x, y на x- 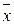, y- 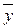имеем:

,

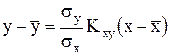После элементарных преобразований уравнения линейной регрессии может быть записано в виде:

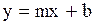(П.21)

где 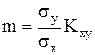; 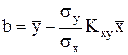(П.22)

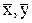- математические ожидания x, y;

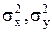- дисперсия x, y;

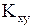- коэффициент корреляции между x и y.

Погрешность определения линейной регрессии определяется дисперсией невязки:

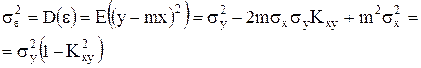(П.23)

Удобно использовать относительное значение дисперсии:

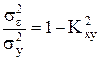(П.24)

Качество линейной регрессии тем лучше, чем ближе к нулю величина . При коэффициенте корреляции 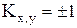получим и тогда между y и x имеется точная линейная связь.