Элементы теории вероятностей и математической статистики

Для построения портфеля ценных бумаг требуются оценки математических ожиданий эффективности ценных бумаг и ковариационная матрица эффективностей ценных бумаг. Воспользуемся методами эконометрики для оценки математического ожидания и ковариационной матрицы.

Пусть X – случайная величина, в том числе может быть и эффективность какой-либо ценной бумаги. В статистике и в эконометрике, в частности, удобно использовать понятие генеральной совокупности и выборки.

Генеральная совокупность – это множество всех возможных значений случайных величин X.

Из генеральной совокупности X последовательно выбирается n значений случайных величин 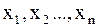. Множество значений случайных величин 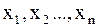называется выборкой объема n случайной величины X.

Имея выборку, можно построить оценку математического ожидания или выборочное математическое ожидание в виде среднего арифметического:

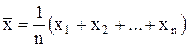(П.1)

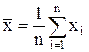или (П.2)

Как связаны выборочное математическое ожидание и истинное математическое ожидание генеральной совокупности?

Пусть генеральная совокупность имеет математическое ожидание 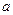и дисперсию 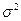. Если предполагать, что производится оценка математического ожидания по формуле (П.1) для всевозможных выборок длины n из генеральной совокупности, то оценка 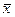становится случайной величиной. Можно доказать, что математическое ожидание 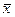совпадает с истинным математическим ожиданием генеральной совокупности, т. е.:

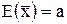(П.3)

Действительно, в (П.1) 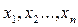будут случайными величинами с математическим ожиданием .

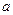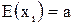, где i=1,2…,n

Тогда имеем: 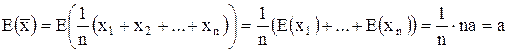ч. т. д.

Свойство (П.3) называют несмещенностью оценки математического ожидания.

Оценка дисперсии может быть произведена по формуле:

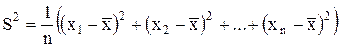(П.4)

или

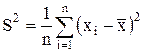(П.5)

Расчет удобно производить по формулам:

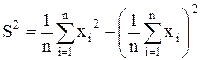(П.6)

Оценки (П.4) и (П.6) являются смещенными.

Для дисперсии случайной величины несмещенной оценкой будет:

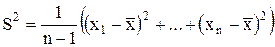(П.7)

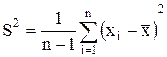или (П.8)

Точнее, можно доказать, что 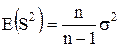, что и означает несмещенность оценки дисперсии (П.7), (П.8). Доказательство этого факта достаточно громоздко и опущено в данном изложении.

Несмещенные оценки необходимо использовать при небольшом объеме выборки.

1) Свойства математического ожидания:

1. 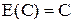, где С – постоянная;

2. 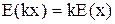, где k постоянный коэффициент;

3. ,

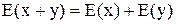в частности, .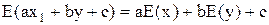

2) Свойства дисперсии:

1. 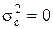, где c – постоянная;

2. 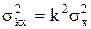, где k - постоянный коэффициент;

3. 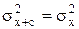, где c – постоянная;

4.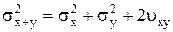 ,где v_xy – ковариация случайных величин x и y.

Ковариация

Пусть x, y – две случайные величины. Оценка ковариации имеет вид:

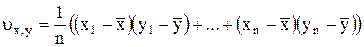(П.9)

или 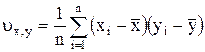(П.10)

Вычислять ковариацию удобнее по формуле:

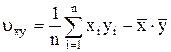(П.11)

Оценка ковариации (П.9), (П.11) смещенная, точнее имеет место 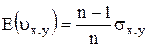. Отсюда следует, что несмещенная оценка для ковариации получится при замене в формулах (П.9), (П.11) множителя 1/n на 1/(n-1) т. е.

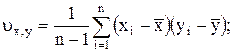(П.12)

Размерность ковариации равна произведению размерностей случайных величин x и y. Коэффициентом корреляции называется безразмерная величина равная:

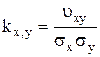(П.13)

где

;

;

.

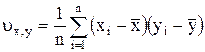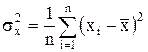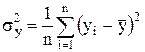Коэффициент корреляции изменяется в пределах от -1 до 1: .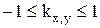

При расчете коэффициента корреляции могут быть использованы смещенные и несмещенные оценки, при этом коэффициент корреляции не изменится.

1) Свойства ковариации:

1.

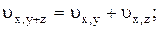
2. 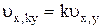, где k - постоянный коэффициент;

3. 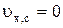, где c – постоянная;

2) Свойства коэффициента корреляции:

1. 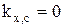, где c – постоянная;

2. 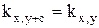, где c – постоянная;

3. 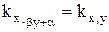при β>0 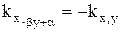при β<0.

Следовательно:

1.

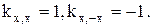
2.

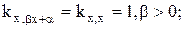
3. .

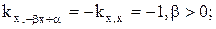Не вдаваясь в тонкости математической статистики можно утверждать, что чем больше длина выборки, тем точнее определяются параметры. Если число параметров и объем выборки сравним, то параметры определить невозможно. Если длина выборки в 1,5÷2-10 раз больше числа параметров, то они определяются достаточно точно.