Метод ведущих факторов

В экономической жизни все взаимосвязано, но есть факторы, которые влияют сразу на все показатели. Таких факторов может быть несколько. Например, цены на энергоносители, недвижимость, кредиты и т. д. Рассмотрим один из таких ведущих факторов, не определяя пока его природу.

Пусть R 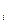- эффективность i-ой ценной бумаги, F-ведущий фактор фондового рынка. Будем считать, что эффективность всех вложений зависит от него. Простейшая зависимость линейна (см. рис. 9.1.). Примем гипотезу:

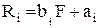+ε_i, (9.1)

где ε_i - случайные погрешности линейного представления эффективности i-ой ценной бумаги R 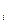через ведущий фактор F. Предполагается, что математические ожидания погрешностей равно нулю E(ε_i) = 0. и погрешности ε_i и ε_j попарно взаимно некорелированы E(ε_i · ε_j) = 0 и некорелированы с ведущим фактором E(ε_i · F) = 0.

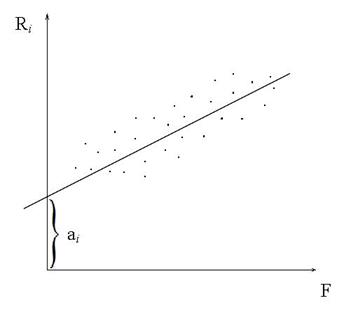
Рис.9.1.

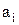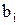Определить постоянные значения и можно по синхронным измерениям эффективностей R₁, R₂, … R_n, и ведущего фактора F методом наименьших квадратов, т. е. построить линейную парную регрессию (см. приложение).

Тогда, из (9.1) при известных 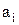, , 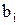известном математическом ожидании m_F и дисперсии 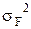ведущего фактора F и известной дисперсии погрешности 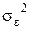могут быть получены оценки для математических ожиданий эффективностей ценных бумаг:

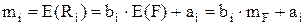(9.2)

Вычитая из (9.1) формулу (9.2) получим:

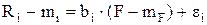
Следовательно, дисперсия эффективности ценной бумаги будет равна:

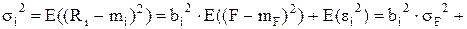
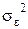(9.3)

Для ковариаций соответственно получим:

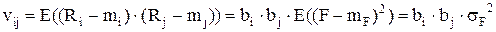(9.4)

Таким образом, полученные математические ожидания эффективностей ценных бумаг (9.2) и элементы ковариационной матрицы (9.3) и (9.4) могут быть использованы для построения оптимальных портфелей ценных бумаг.

ЗАКЛЮЧЕНИЕ

В заключении отметим, что в СЗАГС разработаны и используются в учебном процессе специализированные программы для финансовых расчетов и оценок финансовых рисков. Кроме того, в СЗАГС имеются методики, позволяющие решать указанные выше задачи универсальными программными математическими средствами Matcad, Matlab и Maple.

ПРИЛОЖЕНИЕ