Индивидуальное задание. 1 Доказать утверждение, предъявив формальный вывод из гипотез или аксиом, предварительно проверив выводимость заключения с помощью теоремы о полноте
1 Доказать утверждение, предъявив формальный вывод из гипотез или аксиом, предварительно проверив выводимость заключения с помощью теоремы о полноте. Можно пользоваться теоремой дедукции и её обращением.
1.1(A → (C → B)), (D → A), C ├ (D → B);
1.2(A → B), (A → C) ├ (A → (B & C));
1.3(A → B) ├ ((A → B)Ú B);
1.4(B → A) ├ ((A Ú B)→ A);
1.5(A → B), (B → C) ├ (A → C);
1.6(A → (B → C))├ (B → (A → C));
1.7(A → (ØB)) ├ (B → (ØA));
1.8├ ((A → (ØB)) → (B → (ØA)));
1.9├ ((A Ú A) → A);
1.10A, B ├ (B & A).
1.11А├ (А → (B →A));
1.12А →B ├ А→А;
1.13B├ А→А;
1.14 ├ А→А;
1.15А , B ├ А→B.
Метод резолютивного вывода
Алгоритмы доказательства выводимости А⊦B, построенные на основе этого метода, применяются во многих системах искусственного интеллекта, а также являются фундаментом, на котором построен язык логического программирования «Пролог».
Идея метода резолюций заключается в том, что доказательство истинности или ложности выдвинутого предположения, например:
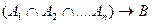
ведется методом от противного. Для этого в исходное множество предложений включают аксиомы формальной системы и отрицание доказываемой гипотезы:
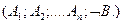
Если в процессе доказательства возникает противоречие между отрицанием гипотезы и аксиомами, выражающееся в нахождении пустого списка (дизъюнкта), то выдвинутая гипотеза правильна. В методе резолюций множество предложений обычно рассматривается как составной предикат, содержащий несколько предикатов, соединенных логическими функциями и кванторами существования и общности. Так как одинаковые по смыслу предикаты могут иметь разный вид, то предложения преобразуются в клаузальную форму – разновидность конъюнктивной нормальной формы, в которой удалены кванторы существования, всеобщности, символы импликации, равнозначности и др. Клаузальную форму называют сколемовской конъюнктивной формой.
В клаузальной форме вся исходная логическая формула представляется в виде множества предложений (клауз) С, называемых клаузальным множеством:
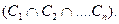
Любое предложение, из которого образуется клаузальное множество, является совокупностью атомарных предикатов или их отрицаний, соединенных символом дизъюнкции:
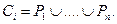
Предикат или его отрицание называется дизъюнктом, литералом, атомом, атомарной формулой.
Сущность метода резолюций состоит в проверке того факта, содержит ли клазуальное множество пустое предложение, если не содержащее литер. Если клазуальное множество содержит пустое предложение, то множество противоречиво (невыполнимо).
Контрарная пара литер 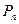 и
и 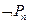 удаляется из множества, а из оставшихся частей формируется новое предложение (например из
удаляется из множества, а из оставшихся частей формируется новое предложение (например из 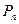 и
и 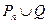 выводится
выводится 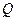 ).
).
Предложение, вновь сформированное из клауз называется резольвентой.
Например, из клауз:
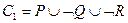 ,
,
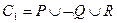 ,
,
получится резольвента 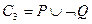 .
.
Если при выводе предложений получены два однолитерных дизъюнкта, образующих контрарную пару, то их резольвентой будет пустой дизъюнкт. Так как наличие пустого дизъюнкта означает, что клазуальное множество является ложным, то невыполнимость исходного утверждения, сформулированного в виде отрицания, доказывает истинность выдвинутого предположения.
Алгоритм метода резолюций в исчислении высказываний
1. Каждый дизъюнкт из КНФ представим в виде 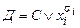 , где С - переменные, входящие в дизъюнкт, xi - выделенная переменная с отрицанием
, где С - переменные, входящие в дизъюнкт, xi - выделенная переменная с отрицанием 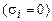 , либо без отрицания
, либо без отрицания 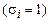 .
.
2. Выбираем контрарную пару дизъюнктов, редуцируем новый дизъюнкт:
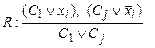 .
.
Пара дизъюнктов редуцировалась в дизъюнкт 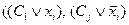 ⊦
⊦ 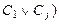 .
.
3. Образуем новый список дизъюнктов из дизъюнктов вида: 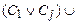 (оставшийся список дизъюнктов). Такой список называется редуцированным.
(оставшийся список дизъюнктов). Такой список называется редуцированным.
4. Применяем правило R применяют к редуцированному списку дизъюнктов.
Остановка наступает, когда в списке остаются только два дизъюнкта вида 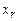 и
и 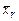 , либо применение R невозможно.
, либо применение R невозможно.
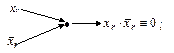
Список дизъюнктов редуцировался в КНФ 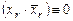 .
.
Алгоритм метода резолюций в исчислении предикатов отличается тем, что формулу логики предикатов необходимо привести к сколемовской форме, затем матрицу формы (предикаты без кванторов) привести к КНФ с помощью законов упрощения формул. После чего также выделяется список дизъюнктов, к которому применяется правило резолюций.
Пример. Методом резолюций проверить выводимость формулы
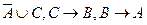 ├
├ 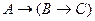 .
.
Решение:
Выводимость данной формулы по методу резолюций следует из противоречивости множества
Г: 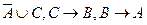 ,
, 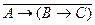 .
.
Приведем все формулы из Г к КНФ:
Г: 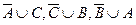 ,
, 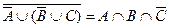 .
.
Клазуальное множество дизъюнктов:
S: 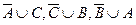 ,
, 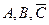 .
.
Построим возможный резолютивный вывод нуля (пустого дизъюнкта) из Г:
1.res 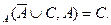
2.res 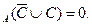
Пустой дизъюнкт получен, следовательно набор формул Г противоречив, откуда следует, что формула 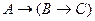 выводима из гипотез
выводима из гипотез 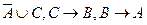 .
.
Упражнения
Исследовать выполнимость формулы логики высказываний методом резолюций. Проверить результат по таблице истинности.
1. 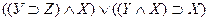 ;
;
2. 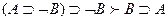 ;
;
3. 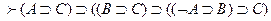 .
.
Дата добавления: 2016-04-11; просмотров: 1452;
