V. Исчисление высказываний.
Наибольший интерес представляет построение формальной системы, которая среди всех возможных ППФ высказываний выделяет такие, которые являются логическими законами (правильно построенными рассуждениями, логическими умозаключениями, тавтологиями, общезначимыми высказываниями).
Формальная система, порождающая высказывания, которые являются тавтологиями и только их, называются исчислением высказываний (ИВ). Выше было показано, что любая формула высказываний (в том числе и тавтология) может быть приведена к структуре рассуждения (умозаключения), «если Р, то S».

Общезначимые
 высказывания (тавтологии)
высказывания (тавтологии)
Формулы в ИВ считаются выводимыми из аксиом. В каждом выводе из тавтологий выводятся тавтологии. Обозначение: 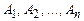 ⊦
⊦  ; интерпретация: из
; интерпретация: из 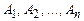 выводимо
выводимо  .
.
Формальная система ИВ определяется:
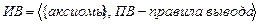
Формулы – аксиомы являются тавтологиями. Правила вывода в виде 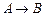 также являются тавтологиями.
также являются тавтологиями.
На сегодняшнее время известно »20 ИВ, которые отличаются друг от друга аксиомами (схемами аксиом) и правилами выводов. Все ИВ обладают 1) свойством полноты – (в них выводимы все тавтологии и только они) 2) набор аксиом обладает минимальной полнотой ( т.е. удаление хотя бы одной аксиомы из набора делает ИВ неполной).
Два примера:
1) ИВ Уйтхеда и Рассела (1920¸1930, Англия).
Аксиомы
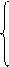 А1. (А Ú А) ® А – закон тавтологии
А1. (А Ú А) ® А – закон тавтологии
А2. А ® (В Ú А) – закон добавления
А3. (А Ú В)®(В Ú А) – закон перестановки
А4. (А Ú В)®((С Ú А) ® (С Ú В)) – закон суммирования
Правила вывода Р1: Подстановка А вместо В; Р2: Замена на эквивалентную формулу 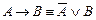 Р3: Modus ponens
Р3: Modus ponens 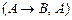 ⊦ В.
⊦ В.
2) ИВ Никоды (1952, США)
Единственная аксиома с операцией штрих Шеффера:
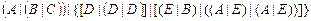 ;
;
единственное ПВ: 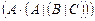 ⊦ С.
⊦ С.
Дата добавления: 2016-03-22; просмотров: 1092;
