Введение в анализ. Дифференциальное исчисление функции одной переменной.
Основные теоретические сведения
1. Схема полного исследования функции и построение ее графика.
Для полного исследования функции и построения ее графика можно рекомендовать следующую примерную схему:
1) указать область определения;
2) найти точки разрыва функции, точки пересечения ее графика с осями координат;
3) установить наличие или отсутствие четности, нечетности, периодичности функции;
4) найти асимптоты графика функции;
5) исследовать функцию на монотонность и экстремум;
6) определить интервалы выпуклости и вогнутости;
7) построить график функции.
2. Правила дифференцирования. Если 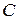 – постоянное число и
– постоянное число и 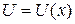 ,
, 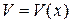 – некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
– некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) 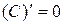 . .
| 2) 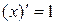 . .
| 3) 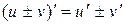 . .
|
4) 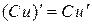 . .
| 5) 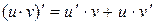 . .
| 6) 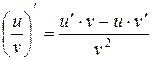 . .
|
3. Таблица производных основных элементарных функций
1. 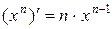 . 2.
. 2. 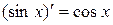 .
.
3. 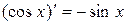 . 4.
. 4. 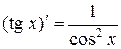 .
.
5. 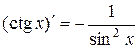 . 6.
. 6. 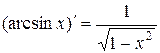 .
.
7. 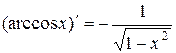 . 8.
. 8. 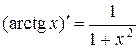 .
.
9. 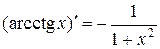 . 10.
. 10. 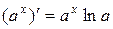 .
.
11. 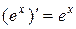 . 12.
. 12. 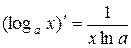 .
.
13. 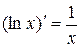 . 14.
. 14. 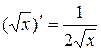 .
.
Пример 1.Найти указанные пределы.
| а) | 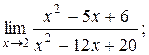
| б) | 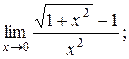
|
| в) | 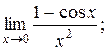
| г) | 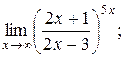
|
Решение:
а) 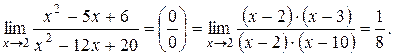
б) 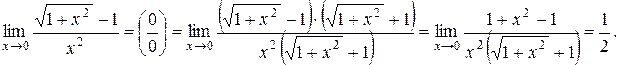 в)
в) 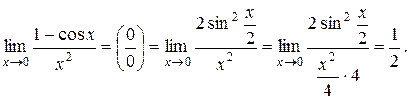
г)
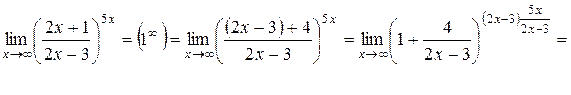
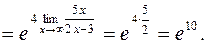
Пример 2.Исследовать функцию 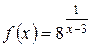 на непрерывность в точках
на непрерывность в точках 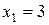 ,
, 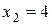 .
.
Решение: для точки x1 = 3 имеем:
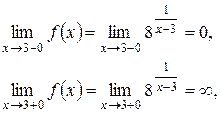
точка 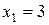 – точка разрыва II
– точка разрыва II
При 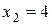 функция определена, следовательно
функция определена, следовательно 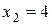 не является точкой разрыва,
не является точкой разрыва, 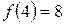 .
.
Пример 3.Найти производную функции 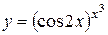 .
.
Решение.Логарифмируя данную функцию, получаем:
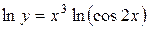 .
.
Дифференцируем обе части последнего равенства по х:
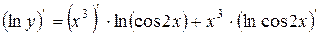 .
.
Отсюда
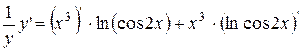 .
.
Далее
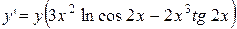 .
.
Окончательно имеем:
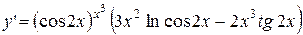 .
.
Пример 4.Найти производную функции y, если 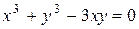 .
.
Дифференцируем обе части данного уравнения по 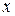 , считая
, считая 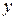 функцией от
функцией от 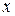 :
:
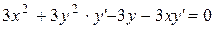 .
.
Отсюда находим
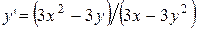 .
.
15. 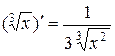 . 16.
. 16. 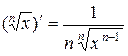 .
.
Дата добавления: 2016-02-16; просмотров: 1523;
