Вариационное исчисление

Вариационные методы позволяют определять функции, доставляющие экстремум

(максимум или минимум) различным функционалам. Основным объектом изучения в вариационном исчислении является функционал “стандартного” вида

J = 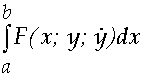, (1.19)

то есть определенный интеграл, зависящий от независимой переменной х, искомой функции у(х) и ее производной .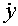

В настоящее время имеется много информации, посвященной вариационным методам. Студент, интересующийся строгими доказательствами, а также желающий получить более обширные знания в области вариационных методов, может непосредственно обратиться к списку литературы, приведенному в конце пособия [3-5 ].

Центральной теоремой вариационного исчисления является теорема Эйлера, дающая необходимое условие того, что функция у(х) доставляет экстремум функционалу (1.19) с граничными условиями у(а) = уа, у(b) = уb среди всех гладких (имеющих непрерывную первую производную 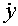) кривых, проходящих через те же точки.

Функционал (1.19) достигает экстремума , если функция у(х) является решением уравнения Эйлера (выведенного в 1744 году):

Fy - 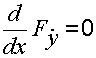, (1.20)

где ; .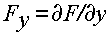

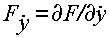Чтобы раскрыть смысл уравнения Эйлера, произведем дифференцирование по х второго члена уравнения (1.20):

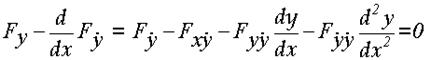. (1.21)

Таким образом, уравнение Эйлера является нелинейным дифференциальным уравнением второго порядка. Смысл уравнения Эйлера заключается в том, что задачу определения функции, доставляющей экстремум функционалу (1.19), оно сводит к хорошо известной задаче интегрирования дифференциального уравнения. Кривые, удовлетворяющие уравнению Эйлера, называются э к с т р е м а л я м и.

В связи с этим основная теорема вариационного исчисления имеет следующую формулировку: если экстремум функционала вида (1.19) существует и достигается среди гладких функций, то он может достигаться только на экстремалях.

Для функционала, зависящего от второй производной, необходимым условием экстремума является выполнение уравнения Эйлера – Пуассона

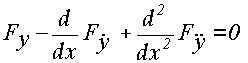, (1.22)

представляющего собой дифференциальное уравнение четвертого порядка.

Сложность решения задачи, поставленной в подразделе 1.1, заключается в том, что для обеспечения минимума расхода топлива необходимо учитывать характеристики всех элементов сложной силовой установки тепловоза: дизеля, электрического генератора, тяговых двигателей, а также законы сопротивления движению подвижного состава.

Если исходить только из характеристик первичного двигателя – дизеля, то оптимальным будет такое управление, при котором поддерживается постоянная мощность дизеля.

С помощью вариационного исчисления можно решить эту задачу при следующих допущениях:

– к.п.д. передачи тепловоза в процессе движения не меняется;

– расход топлива дизелем зависит от мощности линейно по формуле (1.6).

Используя формулы (1.1), (1.6) и (1.7), запишем уравнение движения поезда в виде

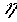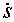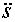1Р = ( + к0 + к1+ к2 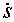2.+ i(s) ). (1.22)

Тогда расход топлива E на прохождение перегона длиной So за время Т будет равен интегралу

Е = 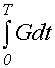= 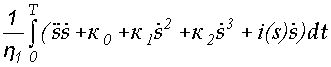, (1.23)

где s – путь, 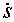– скорость, 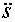– ускорение.

Для определения оптимального закона управления достаточно найти функцию s(t), доставляющую минимум функционалу

J = 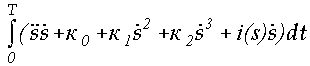. (1.24)

Уравнение Эйлера - Пуассона для функционала (1.24) имеет вид

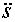(2к1 + 6к2 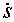) = 0, (1.25)

то есть распадается на два уравнения 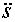= 0 и (2к1 + 6к2 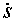) = 0, откуда следует, что 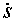= const.

Таким образом, оптимальным по расходу топлива является режим с постоянной скоростью движения тепловоза.

Если уклон не является постоянным (i(s) 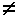const), то постоянство скорости движения может быть достигнуто с помощью регулирования мощности дизеля.

Следовательно, если для дизеля, взятого изолированно, оптимальным является поддержание постоянной мощности, равной номинальной, то при учете всех факторов оптимальным режимом является режим поддержания постоянной скорости.

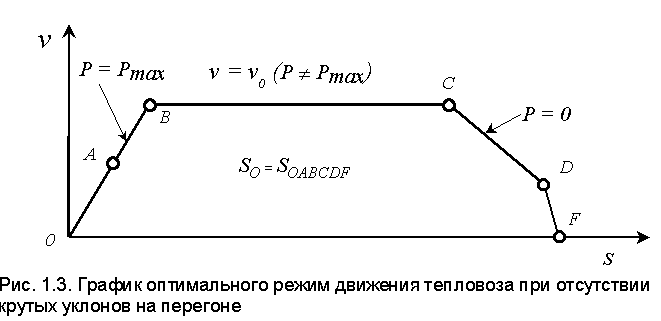
Если сопротивление движению подвижного состава i(s) постоянно, либо меняется в незначительных пределах (уклоны не являются крутыми), то общая структура оптимального режима движения по перегону непосредственно следует из обобщенной теоремы Эйлера: в начальный момент времени, после трогания с места, определяющим является ограничение по максимальному ускорению и осуществление режима 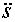= 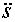max, (участок ОА на рис.1.3).

По мере роста скорости увеличивается и мощность , забираемая от дизеля, и когда эта мощность становится равной максимальной, происходит переход на режим Р = Pmax (участок АВ на рис.1.3). Как только скорость достигнет значения v0, осуществляется переход на частичное использование мощности к движению по экстремали 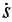= v0. Движение по экстремали продолжается почти до конца перегона (участок ВС на рис.1.3), перед концом движения происходит свободный выбег состава (движение по границе допустимой области Р = 0 - участок CD на рис.1.3), и в самом конце - торможение механическим тормозом.

Величина скорости v0 на участке экстремали выбирается такой, чтобы, с учетом неизбежных участков 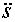= 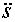max, Р = Pmax и Р = 0, средняя скорость движения по перегону

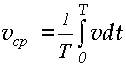
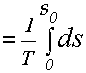(1.26)

равнялась бы заданному значению v ср = 1/ T, то есть площади so, ограниченной кривой 0ABCDF (рис.1.3).

Рассмотрим теперь структуру оптимального управления при наличии крутых подъемов .

Если i(s) велико, то неизбежен провал скорости, и для того, чтобы сохранить прежнее значение интеграла (1.26) нужно увеличить скорость на других участках. Пусть новая скорость тепловоза будет равна v1 = v0 + .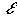

Тогда можно записать

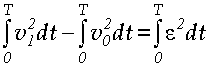. (1.27)

Наименьшее значение интеграла (1.27) будет в том случае, когда функция e (t) станет по возможности симметричной, то есть повышение скорости перед крутым подъемом равно снижению скорости вследствие движения по уклону.

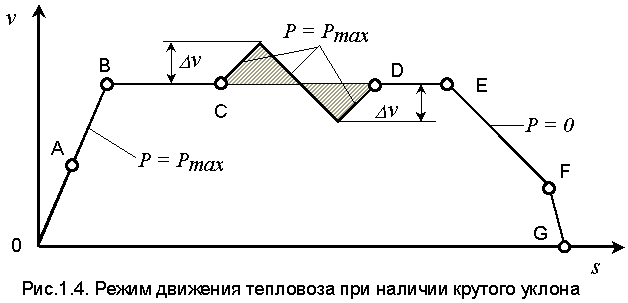
Таким образом, оптимальной оказывается следующая структура движения: перед крутым подъемом переходят на режим Р = Pmax,увеличивая скорость на величину D v (по отношению к v0), равную половине снижения скорости при движении на подъеме (рис.1.4).

Техническая реализация оптимального управления тепловозом следующая. Величиной, которая должна быть известна перед началом движения, является скорость v0 на участках экстремали. Эта скорость определяется путем тягового расчета для заданной массы состава из такого условия, чтобы, с учетом участков разгона и торможения, а также падения скорости на крутых подъемах, средняя скорость движения по перегону в целом равнялась заданной.

Так как скорость v0 вычисляется для расчетной массы состава, которая может отличаться от действительной, а реальная величина сил сопротивления может отличаться от расчетных, то при рассчитанном заранее значении v0 может оказаться невозможным выполнение заданного время хода. Однако ошибки в расчете v0, вызванные неполнотой и неточностью имеющейся информации о массе состава и силах сопротивления движению, могут быть легко исправлены корректировкой.

Алгоритм программы для ЭВМ, реализующий такую корректировку рассматривался автором в работах [ 6-8 ].

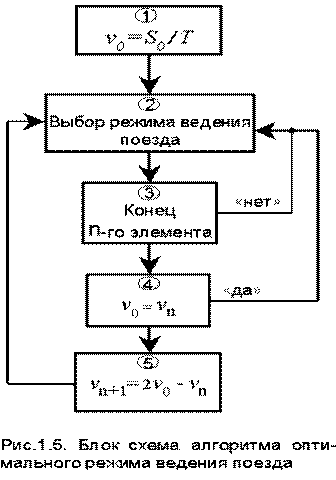
Упрощенная блок-схема алгоритма приведена на рис.1.5.

Блок 1 вычисляет среднюю скорость v0 на участках экстремали. Блок 2 , в зависимости от скорость v0 и профиля пути i(s), определяет необходимую мощность (позицию контроллера машиниста) для поддержания скорости v0. Блок 3 определяет границу n-го элемента профиля пути или перегона. Блок 4 сравнивает заданную скорость движения с действительной средней скоростью на n-м элементе. Если скорость v0 не равна скорости vn, то блок 5 производит корректировку средней скорости для следующего перегона и т.д.

Таким образом, несмотря на то, что на некоторых перегонах средняя скорость может оказаться меньше заданной, график движения по всему участку будет выполнен.

Рассмотрим на конкретном примере разработку оптимального режима ведения поезда тепловозом на перегоне длиной s0 =14,5 км и заданном времени хода T = 27,5 мин (рис.1.6).

Кривую скорости и время хода строим с помощью тяговых расчетов.

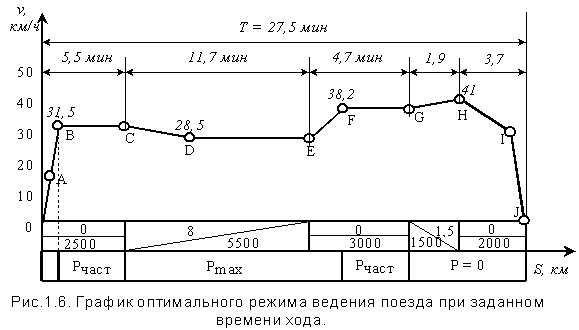
1. Определяем среднюю скорость на перегоне

v0= s0 / T = 14,5 / 0,46 = 31,5 км/ч.

2. Разгоняем поезд до средней скорости 31,5 км/ч, используя сначала частичную, а потом максимальную силу тяги (участок 0AB). Затем до конца первого элемента профиля пути следуем с равномерной (средней) скоростью (линия ВС), используя частичную силу тяги. В конце первого элемента пути поезд имеет скорость 31,5 км/ч и время хода до точки С 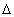t1 = 5,5 мин.

3. Корректируем среднюю скорость движения поезда для оставшейся части перегона s1 = s0 - 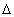s1 = 14,5 - 2,5 = 12 км . Это расстояние должно быть пройдено за время t1 = Т - 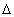t1 = 27,5 - 5,5 = 22 мин (~ 0,37 ч). Следовательно, далее должна быть обеспечена скорость движения

vср2 = 12 / 0,37 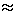32,4 км/ч.

4. Имея начальную скорость для 2-го элемента (i2 = 8 ‰ ) 31,5 км/ч и конечную 28 км/ч, поезд пройдет этот участок, используя максимальную силу тяги за время 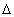t2 = 11,7 мин.

5. Корректируем среднюю скорость движения поезда для оставшейся части перегона

s2 = 14,5 - 2,5 - 5,5 = 6,5 км ;

t2 = 27,5 - 5,5 - 11,7 = 10,3 мин ( 0,17 ч);

vср3= s2 / t2 = 6,5 / 0,17 = 38,2 км/ч.

6. В начале третьего элемента (i3= 0 ‰ , D S3 = 3000 м) реализуется максимальная сила тяги до скорости 38,2 км/ч (отрезок ЕF), а затем до конца элемента сохраняется постоянная скорость. При этом используется частичная сила тяги локомотива. Этот элемент поезд проследует за 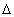t3 = 4,7 мин .

7. Находим среднюю скорость для оставшейся части перегона

s3 = 14,5 - 2,5 - 5,5 - 3 = 3,5 км;

t3 = 27,5 - 5,5 - 11,7 - 4,7 = 5,6 мин (0,093 ч);

vср3= s3 / t3 = 3,5 / 0,093 = 37,6 км/ч.

8. Скорость на четвертом элементе (i4 = -1,5 ‰ , 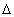S4 = 1500 м.) при реализации режима холостого хода (Р = 0) будет повышаться и к концу элемента достигнет 41 км/ч, а время хода по этому элементу будет равно 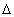t4 = 1,9 мин.

9. Длина оставшейся части перегона 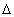S5 = 2000 м. Это расстояние поезд должен пройти за 3,7 мин ( 0,06 ч.)

Для того чтобы этот участок был пройден со средней скоростью

vср5= s5 / t5 = 3,5 / 0,093 = 37,6 км/ч = 33,3 км/ч

поезд должен следовать в режиме холостого хода на отрезке HI, а затем в режиме служебного торможения на отрезке IJ.