ОБЗОР МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПОЕЗДА

О Г Л А В Л Е Н И Е

ВВЕДЕНИЕ

1. ОБЗОР МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПОЕЗДА

1.1. Постановка задачи

1.2. Принцип максимума Понтрягина

1.3. Вариационное исчисление

2. ТЯГОВЫЕ СВОЙСТВА ЛОКОМОТИВОВ С УЧЕТОМ ЭКСПЛУАТАЦИОННЫХ УСЛОВИЙ

2.1. Расчетные характеристики локомотивов

2.2. Снижение коэффициента сцепления локомотивов в кривых малого радиуса

2.3. Влияние атмосферных условий на силу тяги тепловозов

3. СОПРОТИВЛЕНИЕ ДВИЖЕНИЮ ПОДВИЖНОГО СОСТАВА

3.1. Общие сведения

3.2. Основное сопротивление движению

3.3. Дополнительное удельное сопротивление движению от уклона (подъёма или спуска)

3.4. Дополнительное сопротивление от кривой

3.5. Дополнительное сопротивление от низкой температуры окружающего воздуха (ниже – 25 )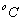

3.6. Дополнительное сопротивление от ветра

3.7. Сопротивление поезда при трогании с места и в начальный период движения

4. РАСЧЕТ МАССЫ СОСТАВА ГРУЗОВОГО ПОЕЗДА В УСЛОВИЯХ ЭКСПЛУАТАЦИИ

4.1. Общие положения

4.2. Выбор расчетного подъема

4.3. Расчет массы состава при движении поезда по расчетному подъему с равномерной скоростью

4.4. Расчет массы состава с использованием кинетической энергии поезда (метод подбора)

4.5. Проверка массы состава по длине приемоотправочных путей

4.6. Расчет массы состава по погонной массе

4.7. Особенности расчета для поездов повышенной массы и длины

4.8. Определение массы состава по условиям удержания поезда на уклоне вспомогательным тормозом локомотива

4.9. Построение тонно-километровой диаграммы

СПИСОК ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

Одним из важнейших факторов, влияющих на расход топлива и электрической энергии на тягу поездов, является правильное управление локомотивом при ведении поезда. Совершенствование методов вождения поезда позволяет существенно и в короткие сроки снизить расход энергоресурсов. После обучения машинистов экономичному вождению поездов расход может быть сокращен на 10 %. Для разработки экономичных режимов управления локомотивом необходимо иметь четкое представление о математических методах оптимального управления движением и возможностях их применения для расчета программ управления локомотивом.

Задача определения оптимального управления движущимся объектом, как правило, решается вариационными методами, которые разделяются на классические вариационные методы, основы которых были разработаны еще в XVIII веке Эйлером и Лагранжем, и новейшие методы, разработанные в последние годы, - динамическое программирование Р.Беллмана и “принцип максимума” Л.С.Понтрягина [ 1 ].

При оптимизации управления движением локомотива можно стремиться к достижению различных целей (критериев оптимальности), и в зависимости от этих целей, рассматривать различные задачи оптимального управления.

Одним из критериев оптимального управления, который часто выступает на первый план, является критерий минимума времени достижения пункта назначения. Управление, оптимальное по этому критерию, называют оптимальным по быстродействию. Такое управление обеспечивает наибольшую провозную способность. По этому критерию производят тяговые расчеты в вычислительных центрах дорог.

Другим критерием является минимизация общих расходов на перевозки, когда известно расписание движения поездов. Суммарные расходы складываются из расходов на амортизацию подвижного состава, потерь на отвлечение груза из оборота на время его транспортировки, зарплаты и расходов на топливо или электроэнергию на тягу. Если время движения задано, то оно определяет составляющие всех расходов, кроме расхода энергоресурсов на тягу. Расход топлива зависит не только от времени движения, но и от закона регулирования скорости на участках движения поезда. Минимизируя расходы на топливо при заданном времени хода, мы минимизируем тем самым и суммарные издержки.

Следует отметить, что управление, оптимальное по критерию минимума суммарных расходов, критерию быстродействия или другим критериям, должно удовлетворять ограничениям по уровню мощности силовой установки, максимальной скорости движения и т.п.

ОБЗОР МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПОЕЗДА

Постановка задачи

Задачу определения оптимального управления движением локомотива при заданном времени хода и минимальном расходе топлива или электроэнергии можно сформулировать следующим образом. Уравнение движения поезда при условии, что масса поезда сосредоточена в центре его тяжести, описывается дифференциальным уравнением

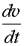= z [ fк(v,u) - w o(v) - i(s)] (1.1)

или, если принять v = ds/dt, то уравнение примет вид

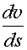= z [ fк(v,u) - w o(v) - i(s)] 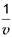, (1.2)

где v – скорость; t – время; s – путь; z – коэффициент; fк – удельная сила тяги; wo – основное удельное сопротивление движению поезда; u – позиция контроллера машиниста; i – сопротивление от плана и профиля пути.

Требуется найти такое управление, при котором достигается минимум расхода энергоресурсов Е, то есть

Е = 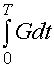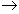min, (1.3)

где Т – фиксированное время хода; G – расход энергоресурсов в единицу времени.

При этом должны соблюдаться следующие ограничения:

1) 0 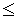F F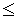max – ограничение по силе тяги локомотива;

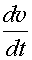
2) 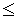dv/dtmax – ограничение по максимальному ускорению;

3) v 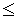vmax – ограничение по максимальной скорости,

при наличии связи

P = 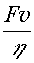, (1.4)

где P – мощность локомотива; 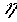– к.п.д. передачи локомотива.

В настоящее время разработано несколько математических методов решения задач оптимального управления движущимся объектом. Рассмотрим основные из них