Принцип максимума Понтрягина
Этот метод, разработанный академиком Л.С.Понтрягиным [ 1 ], при снятии ограничений 2-го и 3-го типа (по скорости и ускорению) и с учетом того, что i(s) = 0, позволяет получить аналитическое решение задачи. Рассмотрим эту задачу на примере тепловозной тяги [ 2 ].
Основное сопротивление движению поезда для заданного подвижного состава зависит только от скорости и определяется выражением
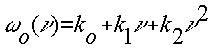 . (1.5)
. (1.5)
С достаточной степенью точности можно считать, что интенсивность расхода топлива линейно зависит от используемой мощности локомотива
Е = 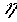 1Р =
1Р = 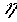 2u, (1.6)
2u, (1.6)
где 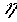 1,
1, 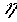 2 – коэффициенты пропорциональности.
2 – коэффициенты пропорциональности.
Обозначив s = x, v = 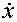 ,
, 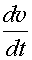 =
= 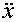 , с учетом формул (1.1) - (1.6) и рационального выбора единиц измерения, запишем уравнение движения поезда в безразмерном виде
, с учетом формул (1.1) - (1.6) и рационального выбора единиц измерения, запишем уравнение движения поезда в безразмерном виде
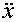 =
= 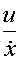 - к0 - к1
- к0 - к1 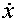 - к2
- к2 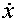 2. (1.7.)
2. (1.7.)
Для удобства записи производные обозначены здесь точками.
Для применения принципа максимума Понтрягина, приняв x = x1 и 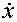 1 = x2 , приведем уравнение (1.7) к виду
1 = x2 , приведем уравнение (1.7) к виду
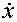 1 = x2;
1 = x2;
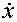 2 = u / x2 - к0 - к1 х2 - к2 х2/2.
2 = u / x2 - к0 - к1 х2 - к2 х2/2.  (1.8)
(1.8)
Необходимо найти такое управление u(t), которое перевело бы систему (1.8) из начального состояния x1(0) = x10 и х2(0) = x20 в конечное x1(Т) = 0 и x2(Т) = 0, обеспечивая при этом минимум функционала (1.3).
Функция Гамильтона [ 1 ] для системы (1.8) запишется в виде
Н(  , x, u) =
, x, u) =  1
1 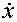 1 +
1 +  2
2 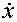 2 , (1.9)
2 , (1.9)
где  1,
1,  2 – вспомогательные переменные, которые определяются выражением
2 – вспомогательные переменные, которые определяются выражением
 i =
i = 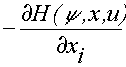 . (1.10)
. (1.10)
Подставляя значения 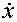 1 и
1 и 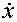 2 из системы (1.8), получим
2 из системы (1.8), получим
Н(  , x, u) =
, x, u) =  1 x1 +
1 x1 +  2 (к0 + к1 x2 + к2 x2/2 -
2 (к0 + к1 x2 + к2 x2/2 - 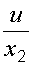 ). (1.11)
). (1.11)
Для оптимальности процесса необходимо, чтобы выполнялось условие максимума:
Н(  , x, u) = max Н(
, x, u) = max Н(  , x, u). (1.12)
, x, u). (1.12)
Как следует из уравнения (1.11) функция Н достигает максимума при u(t) равной  2 / x2 = max. Так как x2 > 0, то, очевидно, что (1.12) достигает максимума при
2 / x2 = max. Так как x2 > 0, то, очевидно, что (1.12) достигает максимума при
umax, если  2 / x2 > 0 ;
2 / x2 > 0 ;
u = (1.13)
0, если  2 / x2 < 0.
2 / x2 < 0.
Отсюда следует, что оптимальное по расходу топлива управление является кусочно-постоянной функцией, принимающей значения umax или 0 (рис.1.1).
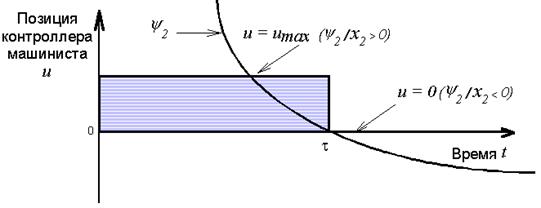
Рис. 1.1 График оптимального по расходу топлива управления тепловозом при отсутствии уклонов
Для определения скорости и момента отключения тяговых двигателей произведем следующие действия. Запишем уравнения для функции yi, используя уравнение (1.10):
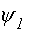 =
= 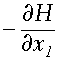 = 0;
= 0;
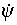 2 =
2 = 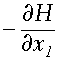 = (к1 + 2 к2 х2. +
= (к1 + 2 к2 х2. + 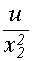 )
)  2 -
2 -  1 (1.14)
1 (1.14)
Из выражения (1.14)  1 = С1. Используя выражения (1.8) и (1.14) составим систему
1 = С1. Используя выражения (1.8) и (1.14) составим систему
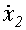 =
= 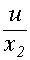 - к0 - к1 х2- к2
- к0 - к1 х2- к2 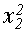 ;
;
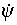 2 =(к1+ 2 к2 x2.+
2 =(к1+ 2 к2 x2.+ 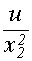 )
)  2 - С1. (1.15)
2 - С1. (1.15)
Функция  2(t) меняется во времени. В начальный момент u = umax. Переключение с umax на u = 0 происходит в момент, когда
2(t) меняется во времени. В начальный момент u = umax. Переключение с umax на u = 0 происходит в момент, когда  2 = 0, значит, после переключения
2 = 0, значит, после переключения  2 < 0, С1 < 0, и поэтому
2 < 0, С1 < 0, и поэтому  2 (t) убывает. Следовательно, функция
2 (t) убывает. Следовательно, функция  2 (t) имеет одно переключение. Исходя из этого, весь фиксированный отрезок времени Т можно разбить на два отрезка [ 0,
2 (t) имеет одно переключение. Исходя из этого, весь фиксированный отрезок времени Т можно разбить на два отрезка [ 0, 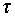 ] и [
] и [ 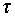 , T ], где
, T ], где 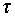 – момент переключения.
– момент переключения.
При u = 0; [ 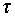 , T ]; t
, T ]; t 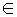 [
[ 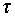 ,T ] получаем
,T ] получаем
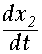 = - к0 - к1х2 - к2
= - к0 - к1х2 - к2 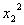 ; -
; - 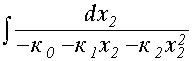 =
= 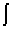 dt ;
dt ;
t = 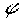 1(x2) + С2;x2(T) = 0; С2 = T -
1(x2) + С2;x2(T) = 0; С2 = T - 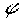 1(0); t =
1(0); t = 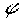 1(x2) + T -
1(x2) + T - 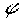 1(0). (1.16)
1(0). (1.16)
При u = umax; [0, 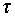 ]; t
]; t 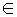 [0,
[0, 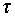 ] получаем
] получаем
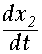 = - к0 - к1х2 - к2
= - к0 - к1х2 - к2 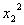 +
+ 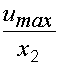 ;
;
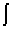 dt = o
dt = o 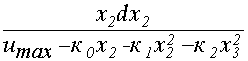 ;
;
t = 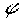 2(x2) + С3; x(0) = 0; С3 =T -
2(x2) + С3; x(0) = 0; С3 =T - 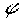 2(0);
2(0);
t = 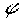 2(x2) -
2(x2) - 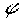 2(0). (1.17)
2(0). (1.17)
В момент 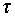 траектория непрерывна, значит
траектория непрерывна, значит
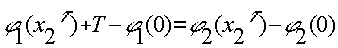 (1.18)
(1.18)
Из выражения (1.18) находится скорость переключения 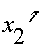 в момент
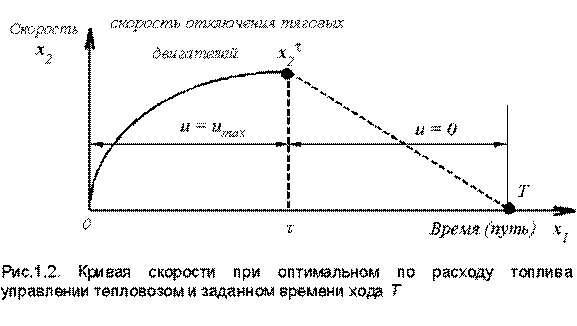
в момент 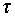 . Подставляя
. Подставляя 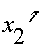 в выражение (1.17), найдем момент переключения
в выражение (1.17), найдем момент переключения 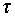 .
.
Процесс, оптимальный по расходу топлива при фиксированном времени хода Т, приведен на рис.1.2. В момент t = 0 включается тяга u = umax для осуществления разгона. При достижении времени 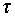 тяга выключается и поезд, двигаясь по инерции, достигает конечную координату за время Т.
тяга выключается и поезд, двигаясь по инерции, достигает конечную координату за время Т.
Дата добавления: 2016-03-05; просмотров: 1960;
