Дифференциальное исчисление функции одной переменной.
3.1. Производная.Рассмотрим функцию у = f(x) определенную на некотором интервале. Дадим аргументу х приращение Dх. Новому значению аргумента х + Dх будет, в общем случае, соответствовать новое значение функции f (x + Dх), т.е. функция также получит некоторое приращение Dу = f (x + Dх) – f (x). Составим отношение 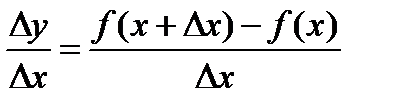 . Если
. Если 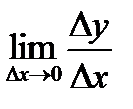 существует, то его называют производной данной функции и обозначаютy` (или f `(x) или dy / dx). Иногда используют обозначение у`х – индекс показывает, по какому аргументу берется производная.
существует, то его называют производной данной функции и обозначаютy` (или f `(x) или dy / dx). Иногда используют обозначение у`х – индекс показывает, по какому аргументу берется производная.
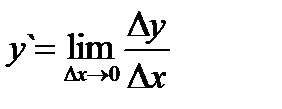 (3.1) или
(3.1) или 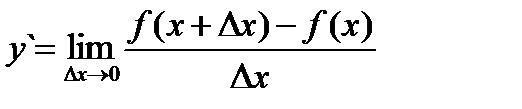 (3.1`)
(3.1`)
Производной данной функции y = f(x) по аргументу х называют предел отношения приращения функции Dу к приращению аргумента Dх, когда последнее произвольным образом стремится к нулю. В общем случае производная также является некоторой функцией от х. (f `(x) = j(x)). Конкретное значение производной при х = а обозначают f `(а) или у`/х = а. Операцию нахождения производной называют дифференцированием функции.
 Понятие производной (и соответствующий математический аппарат) широко используются в различных прикладных задачах. Пример: Известно, что средняя скорость движения тела определяется выражением V = s / t(s = s (t)– путь пройденный телом, t время движения). Очевидно, что мгновенную скорость можно найти, как
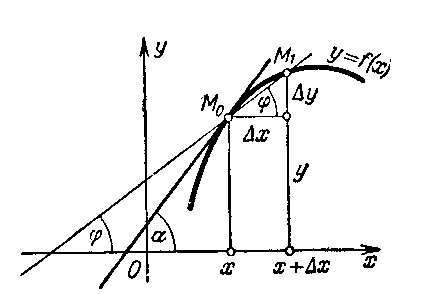
Понятие производной (и соответствующий математический аппарат) широко используются в различных прикладных задачах. Пример: Известно, что средняя скорость движения тела определяется выражением V = s / t(s = s (t)– путь пройденный телом, t время движения). Очевидно, что мгновенную скорость можно найти, как 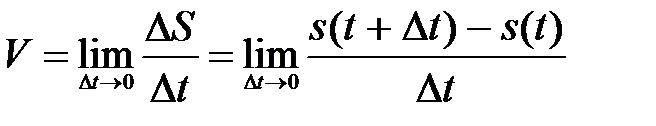 (механический смысл производной). Рассмотрим геометрическую интерпретацию.
(механический смысл производной). Рассмотрим геометрическую интерпретацию.
| Рис. 3.1 |
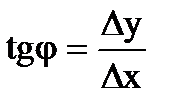 . Если точка М1 приближается к точке М0, то секущая поворачивается вокруг точки М0 (при этом Dх ® 0) и в пределе занимает положение касательной
. Если точка М1 приближается к точке М0, то секущая поворачивается вокруг точки М0 (при этом Dх ® 0) и в пределе занимает положение касательной
к графику функции, проведенной через точку М0.
Угол наклона касательной определится выражением 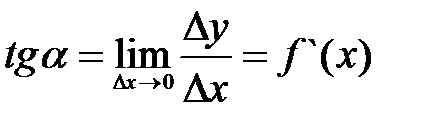 .
.
Геометрический смысл производной очевиден: Значение производной f`(x) при данном значении аргумента х равняется тангенсу угла наклона касательной к графику функции f(x) в соответствующей точке М(х, у). Это, с учетом (1.36), позволяет записать уравнение касательной к кривой у = f(x) в точке (х0, у0) в виде у – у0 = f `(x0)(x – x0) (3.3).
Говорят, что если функция y = f(x) имеет производную в точке х = х0, т.е. если существует предел 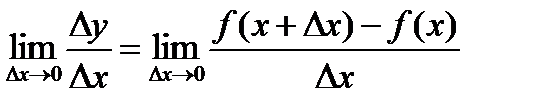 , она дифференцируема в этой точке. Если функция дифференцируема в каждой точке некоторого отрезка (интервала), говорят, что она дифференцируема на отрезке (интервале).
, она дифференцируема в этой точке. Если функция дифференцируема в каждой точке некоторого отрезка (интервала), говорят, что она дифференцируема на отрезке (интервале).
Теорема. Если функция у = f(х) дифференцируема в некоторой точке, то она в этой точке непрерывна. Действительно, если 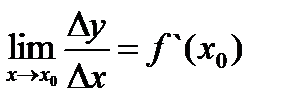 , то
, то 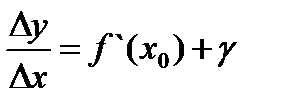 , где g – бесконечно малая величина, т.е.
, где g – бесконечно малая величина, т.е. 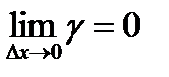 . Но тогда Dу = f `(x0) Dx + gDx, откуда следует, что Dу ® 0 при Dх ® 0 и функция f(x)непрерывна в точке х0. Очевидно, в точках разрыва функция не может иметь производной. Это не значит однако, что если функция непрерывна в точке х0, то она дифференцируема в ней. Рассмотрим функцию, график которой представлен
. Но тогда Dу = f `(x0) Dx + gDx, откуда следует, что Dу ® 0 при Dх ® 0 и функция f(x)непрерывна в точке х0. Очевидно, в точках разрыва функция не может иметь производной. Это не значит однако, что если функция непрерывна в точке х0, то она дифференцируема в ней. Рассмотрим функцию, график которой представлен
| y |
| x |
| в |
| а |
| с |
| y = f(x) |
Рассмотрим функцию 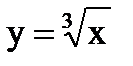 в точке х = 0.
в точке х = 0.  , т.е. в точке х = 0рассматриваемая функция непрерывна, но не дифференцируема.
, т.е. в точке х = 0рассматриваемая функция непрерывна, но не дифференцируема.
Рассмотрим производные основных элементарных функций. Пусть у = х2. Очевидно Dу = (x + Dx)2 – х2 = 2xDx + D2 х и 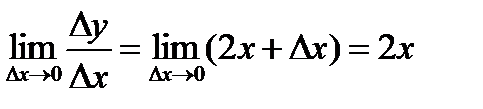 , т.е. если у = х2, то у` = 2х. Рассуждая аналогично, несложно доказать, что производная функции у = хn, где n – целое положительное число, равна nxn–1, т.е. если у = хn, то у` = nхn–1 (3.4). Эта формула, как будет показано ниже, верна и в случае любого действительного n. Приведем без доказательств следующие утверждения:
, т.е. если у = х2, то у` = 2х. Рассуждая аналогично, несложно доказать, что производная функции у = хn, где n – целое положительное число, равна nxn–1, т.е. если у = хn, то у` = nхn–1 (3.4). Эта формула, как будет показано ниже, верна и в случае любого действительного n. Приведем без доказательств следующие утверждения:
Если у = sinx, то y` = cosx (3.5) Если у = cosx, то y` = – sinx (3.6)
Производная постоянной равна нулю, т.е. если у = с, где с – постоянная, то с` = 0 (3.7)
Постоянный множитель можно выносить за знак производной, если у = c f(x), где c = const, то y` = cf `(x) (3.8).
Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций, т.е. если 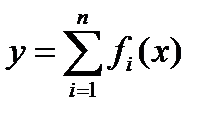 , то
, то 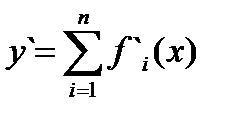 (3.9)
(3.9)
( 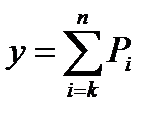 – символ суммы индексированных (нумерованных) величин, где i – текущий индекс, к и n – нижний и верхний пределы суммы – т.е. номера первой и последней складываемых величин.)
– символ суммы индексированных (нумерованных) величин, где i – текущий индекс, к и n – нижний и верхний пределы суммы – т.е. номера первой и последней складываемых величин.)
Производная произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй, т.е. если у = uv, то
y` = u`v + uv` (3.10).
Производная дроби (частного от деления двух функций) равна дроби, знаменатель которой есть квадрат знаменателя данной дроби, а числитель есть разность произведений производной числителя на знаменатель и производной знаменателя на числитель, т.е. если y = u / v, то 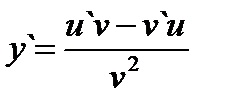 (3.11).
(3.11).
Используя приведенные соотношения можно получить производные других элементарных функций и составить таблицу производных. Приведем их, опуская доказательства.
Если у = logax, то 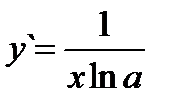 (3.12). Очевидно,
(3.12). Очевидно, 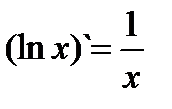 (3.12`)
(3.12`)
Если y = tg x, то 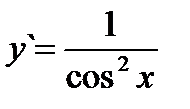 (3.13) Если y = сtg x, то
(3.13) Если y = сtg x, то 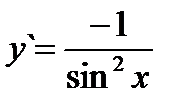 (3.14)
(3.14)
Если у = ах (a > 0), у` = ахln a (3.15) и (ех)` = ex (3.15`)
Рассмотрим особенности нахождения производной от сложной функции - функции вида у = F(u), где u = f(x), или у = F(f(x). Переменную u называют промежуточным аргументом.
Теорема: Если функция u = f(x) имеет в некоторой точке х производную ux` = f `(x), а функция y = F(u), имеет при соответсвующем значении u производную y`u = F(u), то сложная функция у = F(f(x)) в указаной точке х также имеет производную y`х = F`u(u)f `(x) или y`x=y`uu`x (3.16)
(Иначе – производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента).
Пример: y = sin x2 => y = sin u, u = x2, используя (3.16). (3.5) и (3.4) получим: y`u = cos u, u`x = 2x, y`x = 2xcos x2.
Приведенное правило позволяет получить производную неявной функции т.е. функции, заданной уравнением F(x, y) = 0 (3.17).
(Отметим, что если в (3.17) удастся привести уравнение к виду у = f (х), то функция оказывается заданной в явном виде. Операция эта осуществима далеко не всегда).
Пример: F(x, y) = sin (x + y) – e(x – y) = 0. Дифференцируя обе части равенства по х и помня, что у есть функция от х, получим:
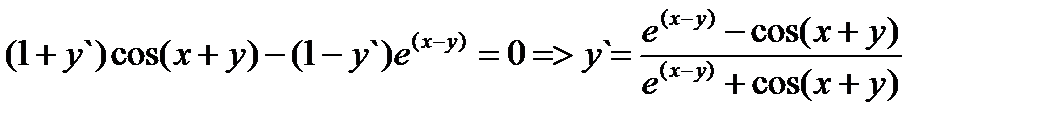
В некоторых случаях, прежде чем найти производную, бывает удобно прологарифмировать уравнение, задающее функцию. Пусть у = хn. Прологарифмировав обе части равенства, получим ln y = n ln x, откуда 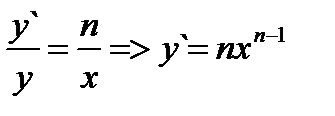 для произвольного действительного n. Выражение
для произвольного действительного n. Выражение 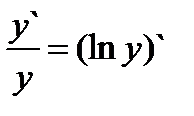 называют логарифмической производной. (Отметим, что логарифмическое дифференцирование удобно применять при нахождении производных от произведения большого количества функций и показательно-степенных функций).
называют логарифмической производной. (Отметим, что логарифмическое дифференцирование удобно применять при нахождении производных от произведения большого количества функций и показательно-степенных функций).
Найдем производную обратной функции. Пусть y = f(x) возрастающая или убывающая функция, определенная на некотором интервале (a, b), (a < b). (Если большему значению аргумента соответствует большее значение функции (f(x2) > f(x1) при x2 > x1) ее называют возрастающей. Если f(x2) < f(x1) при x2 > x1 функция убывающая). Для определенности (без потери общности) рассмотрим возрастающую функцию. Из определения ее очевидно, что значения х и у связывает взаимно однозначное соответствие. Рассматривая у как аргумент, а х как функцию, свяжем их значения соотношением х = j(у). Эта функция является обратной для функции y = f(x), а функция y = f(x) обратной для х = j(у). Эти функции имеют один и тот же график и функция х = j(у)находится как решение уравнения y = f(x) относительно х. Отметим, что:
1. Если возрастающая (убывающая) функция непрерывна на отрезке [a, b], причем f(a) = c, f(b) = d, то обратная функция определена и непрерывна на отрезке [c, d];
2. Если функция y = f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций (однозначных).
Пример: у = х2 на интервале (–¥, ¥) не является ни возрастающей, ни убывающей и имеет две обратные функции: 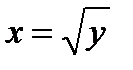 (0 £ х < ¥) и
(0 £ х < ¥) и 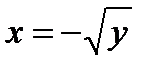 (- ¥ < х < 0).
(- ¥ < х < 0).
Теорема: Если для функции y = f(x) существует обратная функция х =j(у), которая в рассматриваемой точке у имеет производрую j`(у) отличную от нуля, то в соответствующей точке х функция y = f(x) имеет производную f `(x) равную 1 /j`(у), т.е. справедлива формула
f`(x) = 1 / j`(у) (3.18).
Используя полученное правило, пополним таблицу производных:
Если y = arcsin x, то 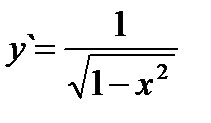 (3.19) Если y = arccos x, то
(3.19) Если y = arccos x, то 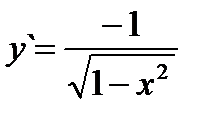 (3.20)
(3.20)
Если y = arctg x, то 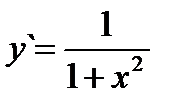 (3.21) Если y = arcctg x, то
(3.21) Если y = arcctg x, то 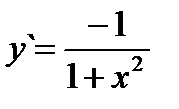 (3.22)
(3.22)
| Примеры: |
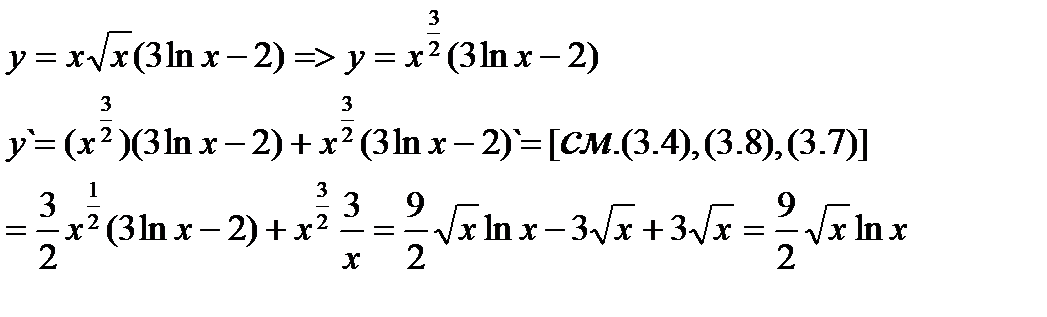
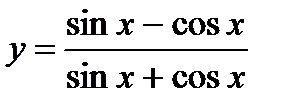 используя (3.11) найдем
используя (3.11) найдем
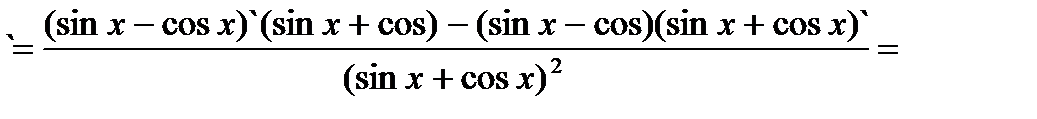 [см. (3.5) и (3.6)] =
[см. (3.5) и (3.6)] =
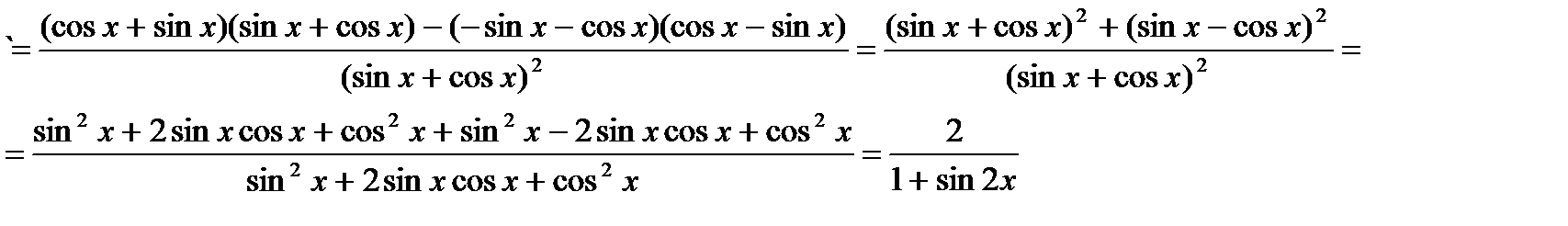
(Напомним, что sin2x + cos2x=1; sin2x = 2sinx cosx)
у = хх. Прологарифмировав обе части равенства по основанию е получим lnу = xlnx. Продифференцировав обе части равенства, найдем (lny)` = (xlnx)` => y`/ у = lnx + 1 => y` = xx (lnx + 1).
Выведем формулу (3.19). Итак, y = arc sin x => sin y = sin arc sin x => x = sin y. Воспользуемся (3.18):
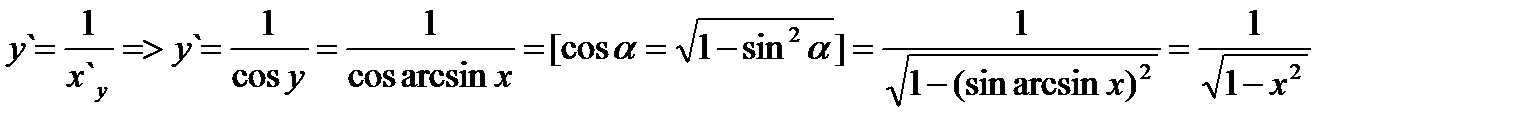
В ряде случаев функциональную зависимость (линию, поверхность) удобно задавать в параметрической форме: каждая неизвестная (координата точки) представляется функцией параметра t, причём каждому значению параметра соответствуют координаты некоторой точки (значения неизвестных, удовлетворяющих обычному уравнению зависимости); 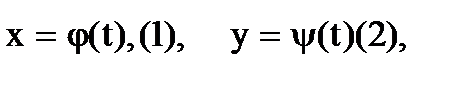 и т.д. (Пример - параметрические уравнения прямой в разделе 1.7.1)
и т.д. (Пример - параметрические уравнения прямой в разделе 1.7.1)
(От параметрического задания функции легко перейти к привычному 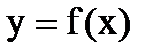 , исключив из уравнений параметр t- разрешив уравнение (1) относительно t и подставив его в (2)). Производная функции, заданной параметрически, определяется выражением:
, исключив из уравнений параметр t- разрешив уравнение (1) относительно t и подставив его в (2)). Производная функции, заданной параметрически, определяется выражением: 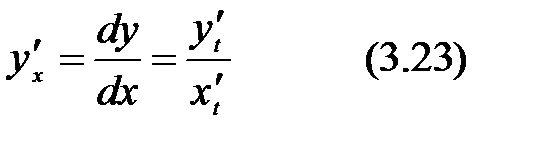
Рассмотрим понятие производных высшего порядка. Производную от функции y = f(x) (ее называют первой), обозначаемую y` = f `(x) = dy / dx можно рассматривать как новую (по отношению к f(x)) функцию той же переменной. Эта функция, в свою очередь, может быть продифференцирована, т.е. найдена первая производная от первой производной исходной функции f(x); (y`)`=(f`(x))`. Она называется второй производной, обозначается y`` = f ``(x)= d2y / dx2 и является производной высшего (второго) порядка. Очевидно, что таким же образом может быть определена производная n–го порядка (n Î Z), обозначаемая y(n) = f(n)(x) (n – берется в скобках, чтобы не путать с показателем степени). Иногда порядок производной обозначают римскими цифрами.
Контрольные вопросы.
1) В чём состоит геометрический, механический смысл производной?
2) Исходя из определения 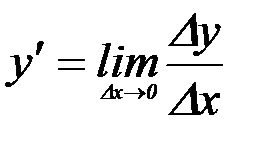 доказать, что
доказать, что 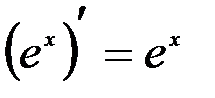 .
.
3) Может ли функция иметь производную в точке, в которой она разрывна?
4) Функция в данной точке дифференцируема. Следует ли отсюда, что она непрерывна в этой точке?
5) Сформулируйте общие правила дифференцирования функции и напишите формулы дифференцирования основных элементарных функций.
6) Как находится производная сложной функции?
7) Как найти производную неявной функции?
8) Что называют обратной функций?
9) Как находится производная обратной функции 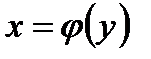 для данной х=f(х), при каких условиях?
для данной х=f(х), при каких условиях?
10) Как находится производная функции, заданной параметрически?
11) Дать понятие производных высшего порядка.
Тест 16.
1) Как называют операцию нахождения производной функции:
а) дифференциалом; б) логарифмированием;
в) потенцированием; г) понижением порядка.
2) Путём вычисления предела 
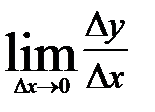 найти производную функции: у=3х2-4х:
найти производную функции: у=3х2-4х:
а) 3х2-4х; б) 6х-х; в) 6х-4; г) 3х2.
3) Используя таблицу производных, правила дифференцирования найти производную сложной функции y=tg3 x2.
а) 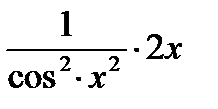 ; б)
; б) 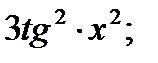 в)
в) 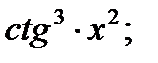 г)
г) 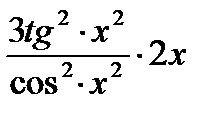 .
.
4) Какая функция является обратной для х=sin y?
а) x=cos y; б) y=cos x; в) x=arcsin y; г) y=arcsin х.
5) Применяя логарифмическое дифференцирование найти производную 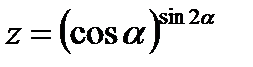 .
.
а) 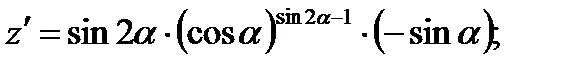
 б)
б) 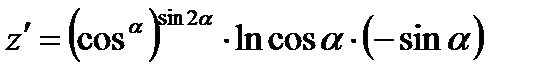 ;
;
в) 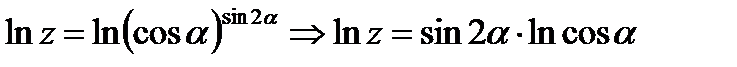
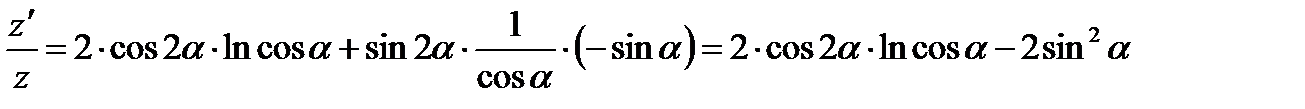
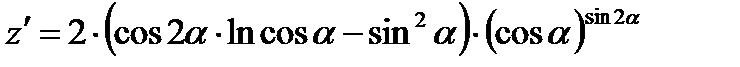
6) Найти производную функции, определив как задана функция: 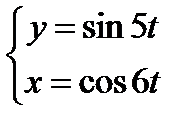 :
:
а) неявно 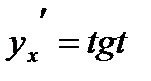 ; б) параметрически
; б) параметрически 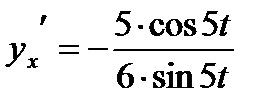 ;
;
в) явно 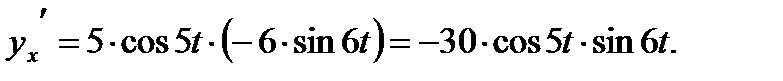
3.2. Дифференциал. Если функция y = f(x) дифференцируема на некотором отрезке, то производная 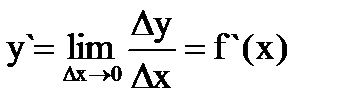 принимает определенные значения. Отношение Dу/DхприDх ® 0можно представить в виде
принимает определенные значения. Отношение Dу/DхприDх ® 0можно представить в виде 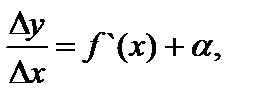 где a ® 0при Dх ® 0. Умножая равенство на Dхполучим Dу = f `(x) Dx + aDx. В общем случае f `(x) ¹ 0 и произведение f `(x) Dх есть величина бесконечно малая одного порядка с Dх, а aDх – бесконечно малая высшего порядка. Первое из двух слагаемых (f`(x) Dх) называют главной частью приращения функции, линейной относительно Dх, или дифференциалом функции и обозначают dy = f `(x) Dх .
где a ® 0при Dх ® 0. Умножая равенство на Dхполучим Dу = f `(x) Dx + aDx. В общем случае f `(x) ¹ 0 и произведение f `(x) Dх есть величина бесконечно малая одного порядка с Dх, а aDх – бесконечно малая высшего порядка. Первое из двух слагаемых (f`(x) Dх) называют главной частью приращения функции, линейной относительно Dх, или дифференциалом функции и обозначают dy = f `(x) Dх .
Пусть у = х. Очевидно, что dy = dx и дифференциал независимого переменного совпадает с приращением и можно записать dy = f `(x)dx (3.24).
Производную функции f `(x) = dy / dx можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
То, что в выражении Dу = dy + aDx второе слагаемое является бесконечно малой более высокого порядка, позволяет в приближенных вычислениях использовать следующий алгоритм:
Dу » f `(х)Dх => f (х+Dх) – f (х) @ f `( x) Dх => f (x + Dх) @ f(x) + f `(x) Dх(3.25.),
причем вычисления тем точнее, чем меньше величина Dх.
Пример: Вычислим приближенное значение sin460; 460 = 450 + 10 = p/4 + p/180; Из (3.25) очевидно, что sin(x + Dх) » sin x + Dх cosx и sin 460 = sin (p/4 + p/180) @ sin p/4 + (p/180)cos p/4 » 0,7194.
Из (3.24) следует, что большинство теорем и формул, относящихся к производной, справедливы и для дифференциалов. Так
d(u + v) = du + dv(3.26), d(uv) = vdu + udv (3.27) и т.д.
| Рис. 3.2 |
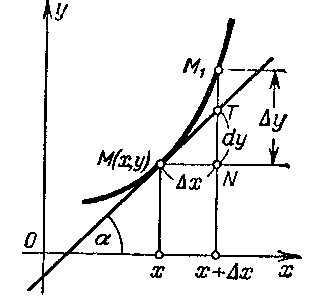 Геометрический смысл дифференциала легко уяснить из рис. 3.2. Возьмем на кривой у = f(x) произвольную точку М(х, у) и проведем касательную. Приращению Dх аргумента соответствует приращение Dу функции и точка М1(х + Dх, у + Dу). Из треугольника МNT находим NT = MN tg a = Dх f `(x) = dy (по определению дифференциала), т.е. геометрически дифференциал представляет собой приращение ординаты
Геометрический смысл дифференциала легко уяснить из рис. 3.2. Возьмем на кривой у = f(x) произвольную точку М(х, у) и проведем касательную. Приращению Dх аргумента соответствует приращение Dу функции и точка М1(х + Dх, у + Dу). Из треугольника МNT находим NT = MN tg a = Dх f `(x) = dy (по определению дифференциала), т.е. геометрически дифференциал представляет собой приращение ординаты
касательной к графику функции в точке М (х,у).
Аналогично тому, как определяются производные высших порядков, определяются и их дифференциалы. Дифференциал от дифференциала называют дифференциалом второго порядка (вторым дифференциалом) и обозначают d(dy) = dy2. По определению дифференциала d2y = [f `(x) dx]`dx = f ``(x)(dx)2, так как dx от х не зависит. Очевидно, таким же образом определяется дифференциал любого порядка dny = f(n)(x)(dx)n; принято записывая порядок дифференциала опускать скобки, т.е окончательно общее выражение примет вид
dny = f(n)(x)dxn (3.24' ).
Контрольные вопросы.
1) Что называют дифференциалом функции?
2) Где применяется 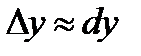 или
или 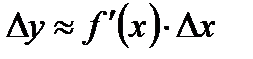 ?
?
3) Как находятся дифференциалы высших порядков?
Тест 17.
1) Найти дифференциал функции: у=х3-3х.
а) 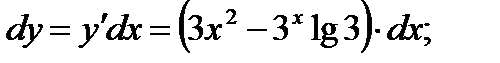 б)
б) 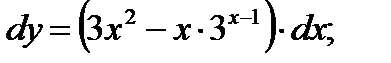 в)
в) 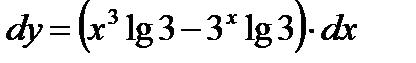
2) Вычислить приближённое значение 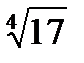 .
.
а) 2,101; б) 2,302; в) 4; г) 2,031.
3.3. Теоремы о среднем. Правило Лопиталя.Приведем (без доказательств) несколько теорем, утверждения которых играют большую роль в аппарате дифференциального исчисления.
1. Теорема Ролля о корнях производной. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в интервале (а, b) и f(a) = f(b), то в интервале (а, b) найдется хотя бы одно значение х =x, при котором f `(x) = 0. Если f(a) = f(b) = 0 (частный случай), то теорема Ролля означает, что между двумя корнями функции содержится хотя бы один корень ее производной. Геометрическое истолкование: если непрерывная на отрезке [a, b] кривая имеет в каждой точке касательную, не параллельную оси Оу, и равные ординаты в точках а и b, то найдется по крайней мере одна точка x (a < x < b) такая, в которой касательная к кривой параллельна оси Ох (tga = f `(x) = 0).
2. Теорема Лагранжа (о конечных приращениях): Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b), то в этом интервале найдется хотя бы одно значение х =x, при котором выполяется равенство f(b) – f(a) = (b – a) f `(x).
Геометрический смысл: на дуге АВ непрерывной кривой у = f(x) имеющей в каждой точке касательную не параллельную оси Оу найдется хотя бы одна точка x (a < x < b) такая, в которой касательная параллельна хорде АВ.
3. Теорема Коши (об отношении приращений двух функций): Если функции f(x) и j(x) непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b), причем j`(x) ¹ 0, то в этом интервале найдется хотя бы одно значение х =x ( a < x < b) такое, что 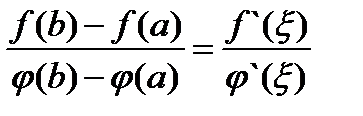 . Теорема Коши позволяет доказать два важных для решения задач теории пределов утверждения, известных под названием правила Лопиталя.
. Теорема Коши позволяет доказать два важных для решения задач теории пределов утверждения, известных под названием правила Лопиталя.
Теорема 1. Пусть функции f(x) и j(x) на некотором отрезке [a, b] удовлетворяют условиям теоремы Коши и обращаются в нуль точке а т.е.
f(a) =j(a) = 0; тогда, если существует 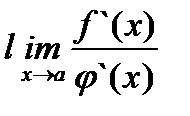 , то существует и
, то существует и 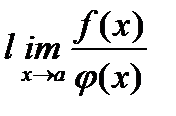 ,
,
причем 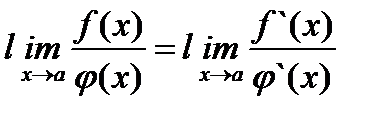 . Это правило позволяет во многих случаях раскрыть неопределенности вида 0/0 (такие, например, как первый замечательный предел), причем: а) теорема справедлива и в случае, когда f(x) и j(x) неопределены при х = а, но
. Это правило позволяет во многих случаях раскрыть неопределенности вида 0/0 (такие, например, как первый замечательный предел), причем: а) теорема справедлива и в случае, когда f(x) и j(x) неопределены при х = а, но 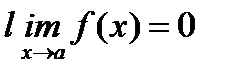 и
и 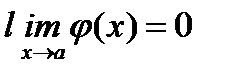 ; б) если f `(a) = j`(a) = 0, а функции f `(x) и j`(x) удовлетворяют условиям теоремы Коши, то, применяя правило Лопиталя дважды, получим
; б) если f `(a) = j`(a) = 0, а функции f `(x) и j`(x) удовлетворяют условиям теоремы Коши, то, применяя правило Лопиталя дважды, получим 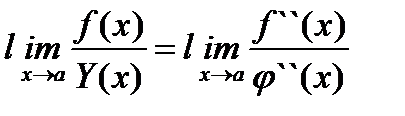 ; в) процедура (при выполнении соответствующих условий) может быть повторяема до получения результата.
; в) процедура (при выполнении соответствующих условий) может быть повторяема до получения результата.
Правило справедливо и в случае 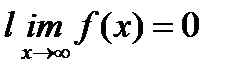 и
и 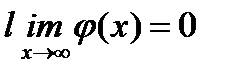 .
.
Теорема 2. Пусть функции f(x) и j(x) удовлетворяют условиям теоремы Коши при всех х¹ а в окресности точки а, 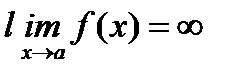 и
и 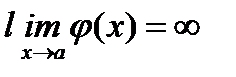 , и пусть существует предел
, и пусть существует предел 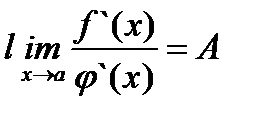 . Тогда существует и предел
. Тогда существует и предел 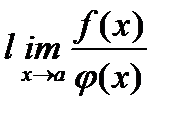 , причем
, причем
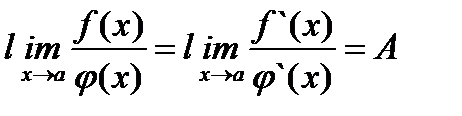 (3.28).
(3.28).
Это правило позволяет раскрывать неопределенности вида 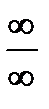 . Оно справедливо и в случаях: а) А = ¥; б) х ® ¥.
. Оно справедливо и в случаях: а) А = ¥; б) х ® ¥.
Во многих случаях это правило позволяет раскрыть неопределенности и других видов, применив предварительно те или иные преобразования. Так, неопределенности вида 0 × ¥ или ¥ – ¥ приводят к виду 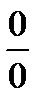 или
или 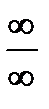 путем алгебраических преобразований данной функции; в случае неопределенности вида 00, ¥0, или 1¥ следует прологарифмировать данную функцию и найти предел ее логарифма.
путем алгебраических преобразований данной функции; в случае неопределенности вида 00, ¥0, или 1¥ следует прологарифмировать данную функцию и найти предел ее логарифма.
Примеры:
1. Неопределенность вида (∞-∞) : 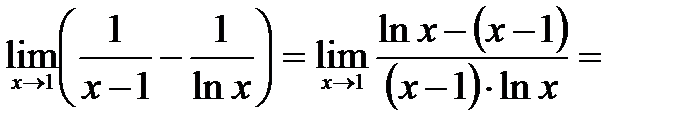 (неопределенность вида
(неопределенность вида 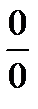 , применяем правило Лопиталя). =
, применяем правило Лопиталя). = 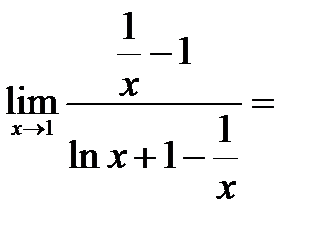 (
( 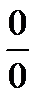 ;правило Лопиталя) =
;правило Лопиталя) = 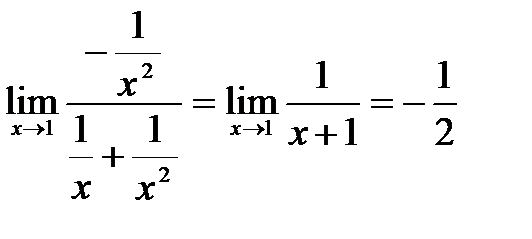
2. Неопределенность вида 00: 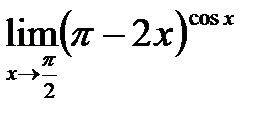 . Обозначим
. Обозначим 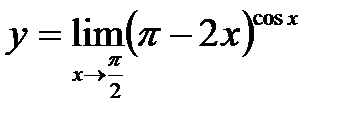 . Прологарифмируем обе части равенства
. Прологарифмируем обе части равенства 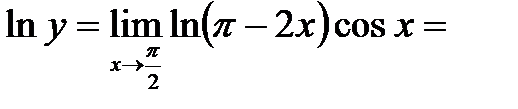 (неопределенность вида ∞·0) =
(неопределенность вида ∞·0) = 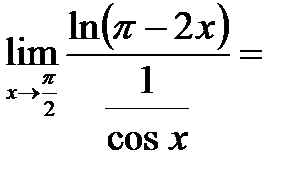 (
( 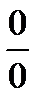 ; правило Лопиталя) =
; правило Лопиталя) = 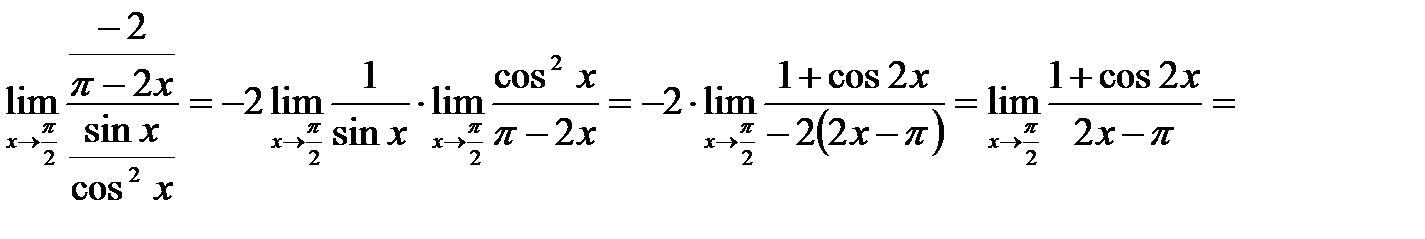 (
( 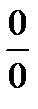 ; правило Лопиталя) =
; правило Лопиталя) = 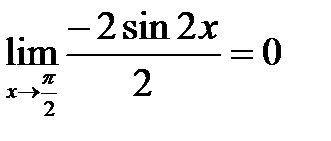 ;
; 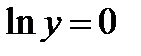 ;
; 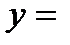 ℮0=1 т.е.
℮0=1 т.е. 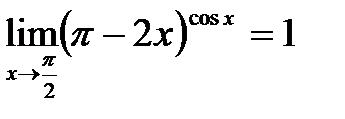 ;
;
Формула Тейлора.Нередко вычисление значений функции y = f(x) при конкретных значениях х оказывается затруднительным. Один из эффективных приемов в этом случае – замена функции степенным многочленом (полиномом) вида: Pn(x – a) = C0 + C1(x – a) + C2(x – a)2 + … + Cn(x – a)n(1) значение которого при х = а равно значению функции f(а). Если функция y = f(x) дифференцируема (n + 1) раз в некоторой окрестности точки а, то коэффициенты Сi можно определить так: потребуем, чтобы в точке а выполнялись условия 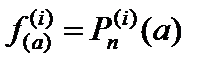 , т.е. чтобы в точке а были равны значения соответствующих производных. Получим:
, т.е. чтобы в точке а были равны значения соответствующих производных. Получим:
f(а)= C0; f `(a) = C1; f ``(a) = 2C2 = C2 ×2! …… ; f(n)(a) = Cn × n!
где n! = n(n –2)(n –3) … (n – k) … 3× 2× 1 (символ n! называется n – факториал). Отсюда легко находятся все 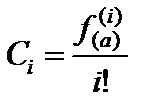 (3.29).
(3.29).
Подставив в (1) получим: 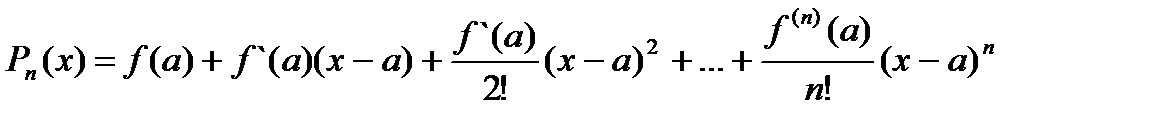 (3.30)
(3.30)
Очевидно, что совпадая при х = а, в других точках значения f(х) и Рn(x) отличаются. Обозначив это отличие через Rn(x) = f(x) – Pn(x) получим:
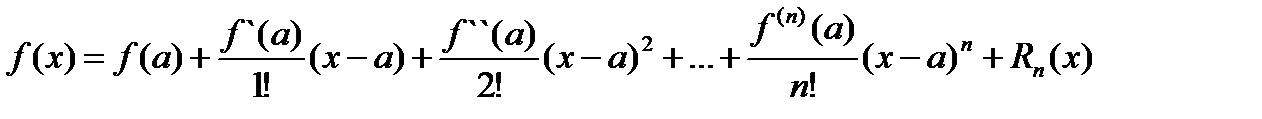 (3.31)
(3.31)
Величину Rn(x) называют остаточным членом. Для значений х, при которых остаточный член мал, многочлен Рn(x) дает приближенное значение f(x). Оценить величину Rn(x) при различных х позволяет выражение
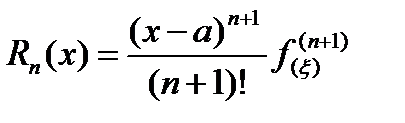 , где a < x < x (3.32).
, где a < x < x (3.32).
(Форма Лагранжа для остаточного члена). Величину x можно представить в виде: x = а + q(х – а), где 0 < q < 1 и тогда (3.32) примет вид
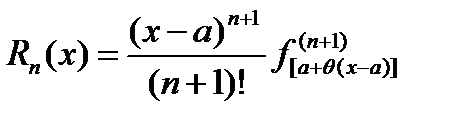 (3.32`)
(3.32`)
(Очевидно, что, если х расположено в достаточно малой окрестности а. величина Rn при достаточно большом n может быть достаточно мала, чтобы обеспечить требуемую точность).
Выражение (3.31), называется формулой Тейлора. Частный случай ее при а = 0 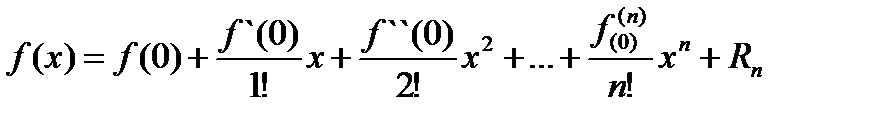 (3.31`)
(3.31`)
где 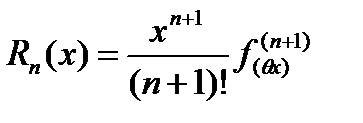 , 0 < q < 1 называется формулой Маклорена. Используя правила дифференцирования, несложно получить разложения многих функций по формуле Маклорена. Приведем некоторые из них:
, 0 < q < 1 называется формулой Маклорена. Используя правила дифференцирования, несложно получить разложения многих функций по формуле Маклорена. Приведем некоторые из них:
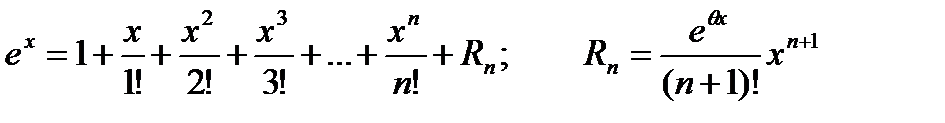 (3.33)
(3.33)
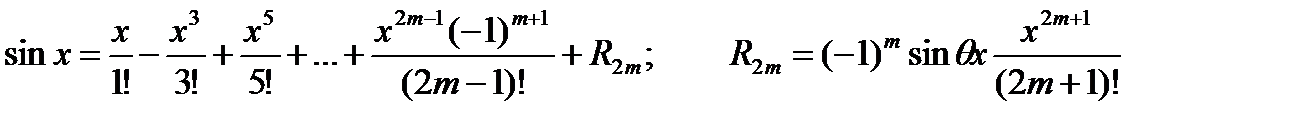 (3.34)
(3.34)
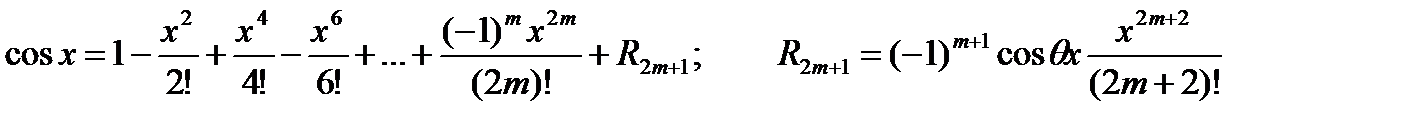 (3.35)
(3.35)
Формула Тейлора может быть применена и для раскрытия неопределенностей вида 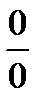 и
и 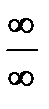 . Функции в числителе и знаменателе дроби «раскладываются» по формуле Тейлора и, после некоторых преобразований, предел вычисляется.
. Функции в числителе и знаменателе дроби «раскладываются» по формуле Тейлора и, после некоторых преобразований, предел вычисляется.
| сокращается; все члены сумм в числителе и знаменателе содержание х (включая остаточные члены в (3.34) и (3.35)) в пределе равны нулю) = 1. |
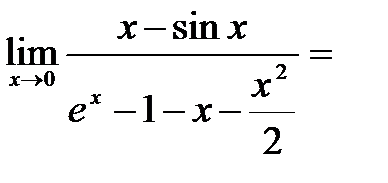 ( с учетом соотношений (3.34) и (3.35)) =
( с учетом соотношений (3.34) и (3.35)) = 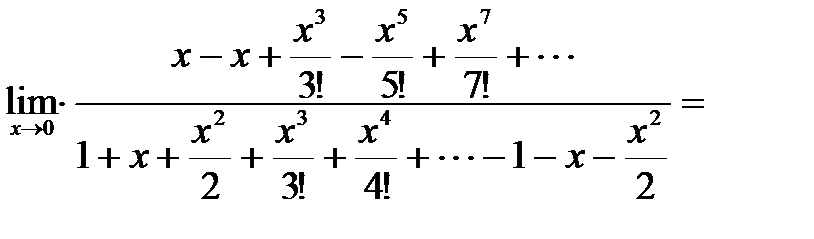
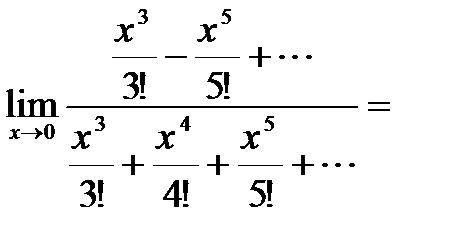
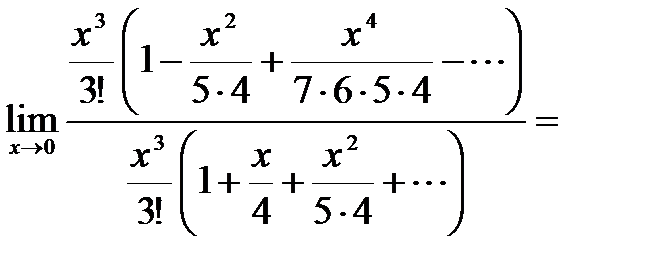 (
( 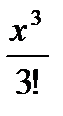
Контрольные вопросы.
1) Какую роль играют в аппарате дифференциального исчисления теоремы Роля, Лагранта, Коши?
2) Можно ли применять правило Лопиталя при неопределённости вида 0; 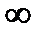 ?
?
3) Можно ли с помощью формулы Тейлора приближённо представить (аппроксимировать) произвольную функцию f(x) в виде многочлена?
4) Как выглядит формула Маклорена?
5) Можно ли с помощью формулы Тейлора для раскрытия неопределённостей вида 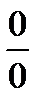 и
и 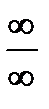 ?
?
Дата добавления: 2016-04-14; просмотров: 1785;
