Предикаты и кванторы
Пусть А – множество объектов произвольной природы (предметная область предиката), n-местный предикат – произвольное отображение
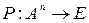 ,
, 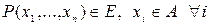 .
.
Пример 1.Предикат A(x) =«x ≤ 2» на множестве X = R – одноместный. Предикат B(x, y) =«xy > 0» на множестве X = 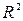 – двуместный.
– двуместный.
Если X = {0,1}, то n-местный предикат является n-местной булевой функцией. Нульместный предикат представляет собой высказывание.
Поскольку множество значений любого предиката лежит во множестве {0,1}, то с предикатами можно производить все операции алгебры логики, и все известные свойства логических операций обобщаются для предикатов. Рассмотрим эти свойства (для удобства в свойствах записываются одноместные предикаты):
1. Коммутативность:
P(x)  Q(x) = Q(x)
Q(x) = Q(x)  P(x), P(x)
P(x), P(x)  Q(x) = Q(x)
Q(x) = Q(x)  P(x).
P(x).
2. Ассоциативность:
P(x)  (Q(x)
(Q(x)  R(x))=(P(x)
R(x))=(P(x)  Q(x))
Q(x))  R(x),
R(x),
P(x)  (Q(x)
(Q(x)  R(x))=(P(x)
R(x))=(P(x)  Q(x))
Q(x))  R(x).
R(x).
3. Дистрибутивность:
P(x)  (Q(x)
(Q(x)  R(x))=(P(x)
R(x))=(P(x)  Q(x))
Q(x))  (P(x)
(P(x)  R(x)),
R(x)),
P(x)  (Q(x)
(Q(x)  R(x))=(P(x)
R(x))=(P(x)  Q(x))
Q(x))  (P(x)
(P(x)  R(x)).
R(x)).
4. Идемпотентность: P(x)  P(x) = P(x), P(x)
P(x) = P(x), P(x)  P(x) = P(x).
P(x) = P(x).
5. Закон двойного отрицания: P(x) = P(x).
6. Закон исключения третьего: P(x)  P(x) = 1.
P(x) = 1.
7. Закон противоречия: P(x)  P(x) = 0 .
P(x) = 0 .
8. Законы де Моргана:
(P(x)  Q(x)) = P(x)
Q(x)) = P(x)  Q(x),
Q(x),
(P(x)  Q(x)) = P(x)
Q(x)) = P(x)  Q(x).
Q(x).
9. Свойства операций с логическими константами:
P(x)  1 = 1, P(x)
1 = 1, P(x)  0= P(x), P(x)
0= P(x), P(x)  1= P(x), P(x)
1= P(x), P(x)  0 = 0.
0 = 0.
Здесь P(x), Q(x) и R(x) – любые предикаты,
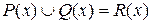 – объединение предикатов,
– объединение предикатов,
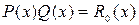 – пересечение предикатов,
– пересечение предикатов,
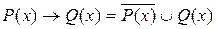 – следствие предикатов,
– следствие предикатов,
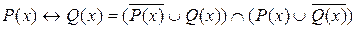 – эквиваленция предикатов.
– эквиваленция предикатов.
Для предикатов определены операции специального вида, которые называются кванторами.
Пусть дан n-местный предикат 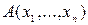 на множестве X, означающий, что для набора
на множестве X, означающий, что для набора 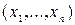 выполнено свойство A, и пусть
выполнено свойство A, и пусть 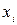 – одна из переменных. Тогда запись
– одна из переменных. Тогда запись 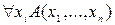 означает, что для всех значений переменной
означает, что для всех значений переменной 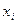 свойство A выполнено. Символ
свойство A выполнено. Символ  называется квантором всеобщности (общности). Предикат
называется квантором всеобщности (общности). Предикат 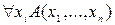 является (n-1)-местным. Он зависит от переменных
является (n-1)-местным. Он зависит от переменных 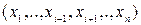 . Если дан одноместный предикат P(x), то утверждение
. Если дан одноместный предикат P(x), то утверждение 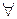 xP(x) представляет собой нульместный предикат, то есть истинное или ложное высказывание.
xP(x) представляет собой нульместный предикат, то есть истинное или ложное высказывание.
Для n-местного предиката 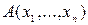 на множестве X и переменной
на множестве X и переменной 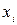 запись
запись 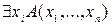 означает, что существует значение переменной
означает, что существует значение переменной 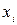 , для которойсвойство A выполнено. Символ
, для которойсвойство A выполнено. Символ 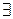 называется квантором существования. Предикат
называется квантором существования. Предикат 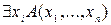 является (n-1)-местным, зависит от переменных
является (n-1)-местным, зависит от переменных 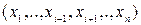 , для одноместного предиката P(x) утверждение
, для одноместного предиката P(x) утверждение  xP(x) представляет собой нульместный предикат, то есть истинное или ложное высказывание.
xP(x) представляет собой нульместный предикат, то есть истинное или ложное высказывание.
Пример 2.На множестве X = R дан предикат A(x) =«x≤2». Высказывание  x(x ≤ 2) – ложно,
x(x ≤ 2) – ложно,  x(x ≤ 2) – истинно.
x(x ≤ 2) – истинно.
Запись  xA (
xA (  xA) не подразумевает, что в формуле A есть переменная x.
xA) не подразумевает, что в формуле A есть переменная x.
Переменная x называется переменной в кванторе, а A – областью действия квантора.
Имеют место эквивалентности:
1) 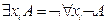 ;
;
2) 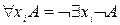 ;
;
3) 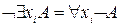 ;
;
4) 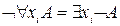 ;
;
5) 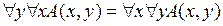 ;
;
6) 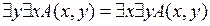 ;
;
7) 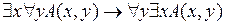 ;
;
8) 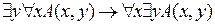 ;
;
9)  x(P(x)
x(P(x) 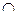 Q(x)) =
Q(x)) =  xP(x)
xP(x) 
 xQ(x);
xQ(x);
10)  x(P(x)
x(P(x)  Q(x)) =
Q(x)) =  xP(x)
xP(x) 
 xQ(x);
xQ(x);
11)  xP(x)
xP(x) 
 xQ(x) =
xQ(x) =  xP(x)
xP(x) 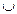
 yQ( y) =
yQ( y) =  x(P(x)
x(P(x) 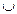
 yQ( y)) =
yQ( y)) =
=  x
x  y (P(x)
y (P(x) 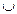 Q( y));
Q( y));
12)  xP(x)
xP(x) 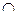
 xQ(x) =
xQ(x) =  xP(x)
xP(x) 
 yQ( y) =
yQ( y) =  x(P(x)
x(P(x) 
 yQ( y)) =
yQ( y)) =
=  x
x  y (P(x)
y (P(x)  Q( y)).
Q( y)).
Предикат тождественно истинный (тождественно ложный), если при всех возможных значениях переменных он принимает значение 1(0).
Пример 3.
Предложение 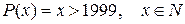 – одноместный предикат, определенный на множестве N.
– одноместный предикат, определенный на множестве N.
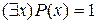 – «существует х, для которого верно
– «существует х, для которого верно 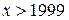 » – истинное высказывание;
» – истинное высказывание;
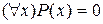 – «для всех x верно
– «для всех x верно 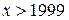 » – ложное высказывание.
» – ложное высказывание.
Предложение 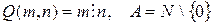 – двухместный предикат, определенный на множестве А.
– двухместный предикат, определенный на множестве А.
Предикат называется выполнимым, если при некоторых значениях переменных он принимает значение истина.
Пример 4.Найти значение высказывания 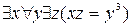 .
.
Трехместный предикат 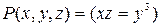 определен на множестве N. Решение:
определен на множестве N. Решение:
Пусть 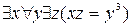 = 1. Эквивалентность имеет место тогда и только тогда, когда для некоторого
= 1. Эквивалентность имеет место тогда и только тогда, когда для некоторого 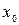
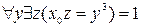 , и предикат
, и предикат 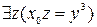 является тождественно истинным относительно y, то есть исходное высказывание истинно.
является тождественно истинным относительно y, то есть исходное высказывание истинно.
Пусть A – формула, 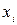 – переменная, которая входит в формулу A (один или несколько раз). Вхождение
– переменная, которая входит в формулу A (один или несколько раз). Вхождение 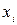 в формулу A называется связанным, если либо
в формулу A называется связанным, если либо 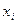 – переменная в кванторе, либо
– переменная в кванторе, либо 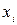 находится в области действия квантора. Если вхождение
находится в области действия квантора. Если вхождение 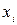 в A не связано, то оно называется свободным.
в A не связано, то оно называется свободным.
В формуле 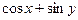 вхождения обеих переменных свободные, в формуле
вхождения обеих переменных свободные, в формуле 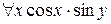 вхождение переменной x связано,а вхождение переменной у свободно.
вхождение переменной x связано,а вхождение переменной у свободно.
Для каждого предиката A областью истинности называется множество Y = {x 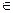 X , A(x) = 1}, на котором предикат принимает значение 1.
X , A(x) = 1}, на котором предикат принимает значение 1.
 Множество истинности предиката
Множество истинности предиката 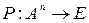 ,
,
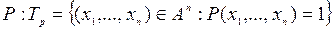 .
.
Для предиката A(x) =«x ≤ 2» на множестве X= 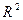 областью истинности является множество Y = {x
областью истинности является множество Y = {x 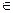 R, x ≤ 2}.
R, x ≤ 2}.
Для предиката B(x, y) =«xy > 0» на множестве X = 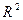 область истинности Y = {(x, y)
область истинности Y = {(x, y) 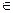
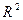 , xy > 0}.
, xy > 0}.
Для области истинности пересечения и объединения предикатов верны соотношения:
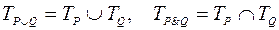 ,
, 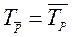 .
.
Следующие предложения означают: 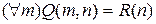 – «для всех m верно: m делится на n» или «любое натуральное ненулевое число делится на n» – одноместный предикат, зависит от n, выполнимый предикат, область его истинности – {n=1}, так как все числа делятся на 1;
– «для всех m верно: m делится на n» или «любое натуральное ненулевое число делится на n» – одноместный предикат, зависит от n, выполнимый предикат, область его истинности – {n=1}, так как все числа делятся на 1;
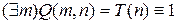 – «существует m, для которого верно: m делится на n» или «найдется натуральное ненулевое число, которое делится на другое натуральное ненулевое число» – одноместный предикат, зависит от n, тождественно истинный предикат, область его истинности – А;
– «существует m, для которого верно: m делится на n» или «найдется натуральное ненулевое число, которое делится на другое натуральное ненулевое число» – одноместный предикат, зависит от n, тождественно истинный предикат, область его истинности – А;
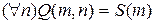 – «для всех n верно: m делится на n» или «натуральное ненулевое число делится на любое натуральное ненулевое число» – одноместный предикат, зависит от m, тождественно ложный предикат, область его истинности –пустое множество;
– «для всех n верно: m делится на n» или «натуральное ненулевое число делится на любое натуральное ненулевое число» – одноместный предикат, зависит от m, тождественно ложный предикат, область его истинности –пустое множество;
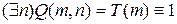 – «существует n, для которого верно: m делится на n» или «натуральное ненулевое число делится на некоторое натуральное ненулевое число» – одноместный предикат, зависит от m, тождественно истинный предикат, область его истинности – А.
– «существует n, для которого верно: m делится на n» или «натуральное ненулевое число делится на некоторое натуральное ненулевое число» – одноместный предикат, зависит от m, тождественно истинный предикат, область его истинности – А.
Упражнения
1. Выделить предикаты, для каждого предиката установить местность и область истинности, если X = R. Для двуместных предикатов изобразить область истинности графически.
1) x + 2 = 0;
2) При x =0 выполняется равенство x − 2 = 0;
3) 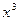 - 8 = 0;
- 8 = 0;
4) 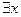 (x - 8 = 0);
(x - 8 = 0);
5) однозначное число x является простым.
2. На множестве M = {1,2,3,…,20} заданы предикаты:
A(x): «x не делится на 5»;
B(x): «x – четное число»;
C(x): «x – число простое»;
D(x): «x кратно 3».
Найдите множество истинности следующих предикатов:
a) 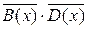 ;
;
b) 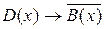 ;
;
c) 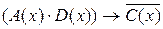 ;
;
d) 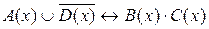 .
.
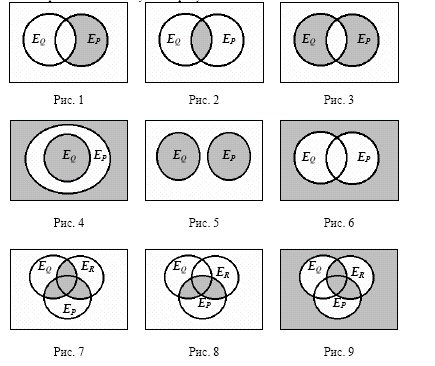
3. Записать предикаты, полученные в результате логических операций над предикатами P(x), Q(x) и R(x), множества истинности которых (E) заштрихованы на следующих рисунках:
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-04-11; просмотров: 3424;
