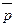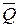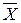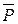Индивидуальное задание. 12. Упростить релейно-контактные схемы:

12. Упростить релейно-контактные схемы:

12.1

12.2

	X

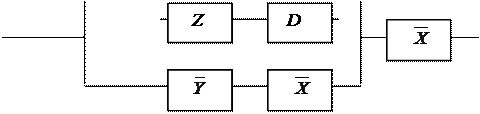12.3

12.4

12.5

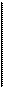
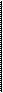
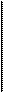
12.7

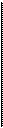
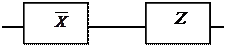
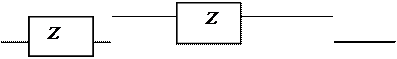12.8

 

 

R

12.9

 

 

Q

12.10

 

 

R

12.11

		R

 

 

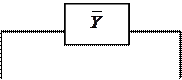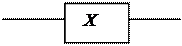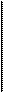
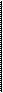
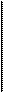
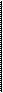
12.12

 

 

 

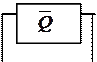
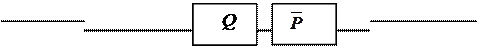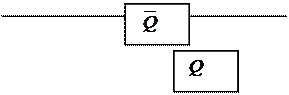12.13

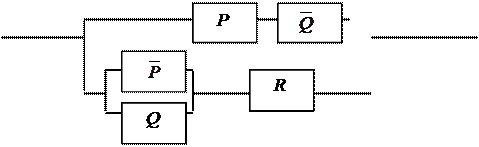13Реализовать схемами следующие формулы:

13.1 ;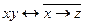

13.2 ;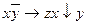

13.3 ;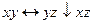

13.4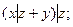

13.5 ;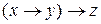

13.6 ;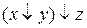

13.7 ;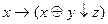

13.8 ;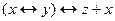

13.9 ;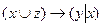

13.10 ;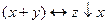

13.11 ;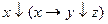

13.12 ;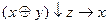

13.12 ;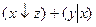

13.14 ;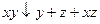

13.15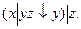

Логические задачи

Логическую задачу можно решить, составляя систему логических уравнений, средствами алгебры логики; с помощью рассуждений.

Обычно используется следующая схема решения:

1) изучается условие задачи;

2) вводится система обозначений для логических высказываний;

3) конструируется логическая формула, описывающая логические связи

между всеми высказываниями условия задачи;

4) определяются значения истинности этой логической формулы;

5) из полученных значений истинности формулы определяются значения истинности введенных логических высказываний, на основании которых делается заключение о решении.

Пример 1. Решить логическую задачу:

«Трое друзей, болельщиков автогонок “Формула-1”, спорили о результатах предстоящего этапа гонок.

«Вот увидишь, Шумахер не придет первым», – сказал Джон. – «Первым будет Хилл».

«Да нет же, победителем будет, как всегда, Шумахер», – воскликнул Ник. – «А об Алези и говорить нечего, ему не быть первым».

Питер, к которому обратился Ник, возмутился: «Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину».

По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?»

Решение:

Введем обозначения для логических высказываний: Ш – победит Шумахер; Х – победит Хилл; А – победит Алези. Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займет этот гонщик, поэтому в дальнейших рассуждениях не учитывается.

Зафиксируем высказывания каждого из друзей: .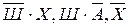

Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание:

;

;

;

;

.

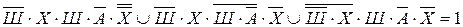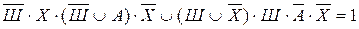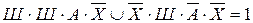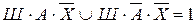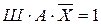Последнее высказывание истинно только при Ш=1, А=0, Х=0.

Ответ: Победителем этапа гонок стал Шумахер.

Пример 2.Решить логическую задачу:

«На вопрос “Кто из трех студентов готовился к экзамену” получен верный ответ “Если готовился Иванов, то готовился и Сидоров, но неверно, что если готовился Петров, то готовился и Сидоров”. Кто готовился к экзамену?»

Решение:

Обозначим простые высказывания «Иванов готовился к экзамену» (Петров, Сидоров) соответственно буквами A (B, C). Тогда условие задачи можно записать в виде формулы .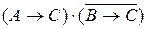

Составные высказывания 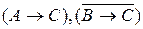(«Если готовился Иванов, то готовился и Сидоров» и «Неверно, что если готовился Петров, то готовился и Сидоров») выполняются одновременно и поэтому они должны быть соединены логической связкой «&» («и»). Выполняя равносильные преобразования, получим:

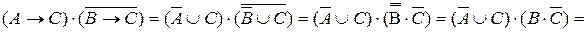
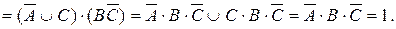
Теперь читаем формулу: «Не готовился Иванов, и не готовился Сидоров, и готовился Петров».

Ответ:к экзамену готовился Петров.

Упражнения

Решить логические задачи:

1. В школе, перешедшей на самообслуживание, четырем старшеклассникам, Андрееву, Костину, Савельеву и Давыдову, поручили убрать 7-й, 8-й, 9-й и 10-й классы. При проверке оказалось, что 10-й класс убран плохо. Не ушедшие домой ученики сообщили о следующем:

1) Андреев: «Я убирал 9-й класс, а Савельев – 7-й».

2) Костин: «Я убирал 9-й класс, а Андреев – 8-й».

3) Савельев: «Я убирал 8-й класс, а Костин – 10-й».

Давыдов уже ушел домой. В дальнейшем выяснилось, что каждый ученик в одном из двух высказываний говорил правду, а во втором ложь. Какой класс убирал каждый ученик?

2. На вопрос «Кто из трех студентов изучал математическую логику?» получен верный ответ «Если изучал первый, то изучал и третий, но неверно, что если изучал второй, то изучал и третий». Кто изучал математическую логику?