Дизъюнктивные и конъюнктивные нормальные формы
Элементарной конъюнкциейназывается конъюнкция переменных высказываний и (или) их отрицаний.
Элементарной дизъюнкциейназывается дизъюнкция переменных высказываний и (или) их отрицаний.
Дизъюнктивной нормальной формой (ДНФ) данной формулы называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.
Конъюнктивной нормальной формой (КНФ) данной формулы называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Для того чтобы построить по данной формуле алгебры логики равносильную ей ДНФ или КНФ необходимо выразить все операции через дизъюнкцию, конъюнкцию и отрицание, воспользоваться законом де Моргана для того, чтобы отрицания стояли лишь над элементарными переменными высказываниями, раскрыть скобки (для построения ДНФ) или воспользоваться дистрибутивным законом (для построения КНФ).
Всякая функция алгебры логики может быть представлена в виде формулы, содержащей только операции конъюнкции, дизъюнкции и отрицания.
Элементарная конъюнкция (дизъюнкция) называется правильной,если в нее каждая переменная входит не более одного раза, включая ее вхождение и под знаком отрицания.
Элементарная конъюнкция (дизъюнкция) называется полной относительно переменных x, y, z, если в нее входит каждая из этих переменных не менее одного раза, включая и их вхождение под знаком отрицания.
Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных x, y, z, называется дизъюнктивная нормальная форма, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильные и полные относительно переменных x, y, z.
Совершенная дизъюнктивная нормальная форма (СДНФ) для булевой функции 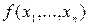 , не равной тождественно нулю, имеет вид:
, не равной тождественно нулю, имеет вид:
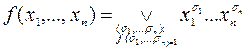 ,
,
где символ  определяется следующим образом:
определяется следующим образом:
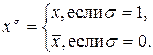
Алгоритм построения СДНФ:
1) построить таблицу истинности данной булевой функции;
2) единичному значению булевой функции будет соответствовать элементарная конъюнкция 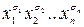 , где
, где 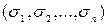 – соответствующий набор значений переменных. В конъюнкции мы записываем
– соответствующий набор значений переменных. В конъюнкции мы записываем 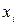 , если
, если 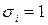 , и
, и 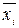 , если
, если 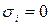 . Элементарные конъюнкции соединяются знаком «
. Элементарные конъюнкции соединяются знаком «  ».
».
Совершенной конъюнктивной нормальной формой (СКНФ) относительно переменных x, y, z, называется конъюнктивная нормальная форма, в которой нет одинаковых элементарных дизъюнкций и все элементарные дизъюнкции правильные и полные относительно переменных x, y, z.
Совершенная конъюнктивная нормальная форма (СКНФ) для функции 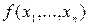 , отличной от тождественной единицы, имеет вид:
, отличной от тождественной единицы, имеет вид:
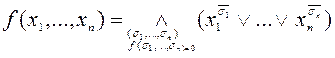 .
.
Алгоритм построения СКНФ:
1) построить таблицу истинности данной булевой функции;
2) каждому нулевому значению булевой функции будет соответствовать элементарная дизъюнкция 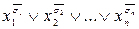 , где
, где 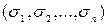 – соответствующий набор значений переменных. В дизъюнкции мы записываем
– соответствующий набор значений переменных. В дизъюнкции мы записываем 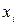 , если
, если 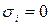 , и
, и 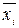 , если
, если 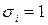 . Дизъюнкции соединяются знаком «
. Дизъюнкции соединяются знаком « 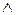 ».
».
Алгоритмы переходов от одной формы к другой:
а) переход от ДНФ к КНФ: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
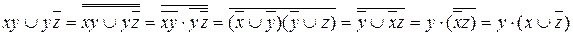 .
.
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки.
б) переход от КНФ к ДНФ: осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения):
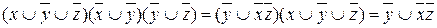 .
.
Таким образом, получили ДНФ.
в) переход от ДНФ к СДНФ: если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение 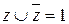 , после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем):
, после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем):
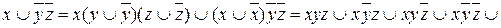
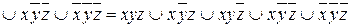 .
.
г) переход от КНФ к СКНФ осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение 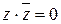 (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
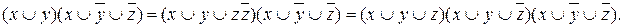 Таким образом, из КНФ получена СКНФ.
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Пример 1.Привести к СКНФформулу (x Ù (y ® z)).
Решение:
x Ù (y ® z) « x Ù (Øy Ú z) – КНФ,
x Ú (y Ù Øy) Ù (Øy Ú z) Ú (x Ù Øx) « (x Ú y) Ù (x Ú Øy) Ù (Øy Ú z Ú x) Ù Ù(ØyÚ z Ú Øx) « (x Ú y) Ú (z Ú Øz) Ù (x Ú Øy) Ú (z Ú Øz) Ù (Øy Ú z Ú x) Ù Ù(Øy Ú Ú z Ú Øx) « (x Ú y Ú z) Ù (x Ú y Ú Øz) Ù (x Ú Øy Ú z) Ù (x Ú Øy Ú ÚØz) Ù (Øy Ú z Ú x) Ù (Øy Ú z Ú Øx).
Пример 2.Привести к СКНФформулу ((x Ù y) ® (x Ù z)).
Решение:
(x Ù y) ® (x Ù z) « Ø(x Ù y) Ú (x Ù z) « (Øx Ú Øy) Ú (x Ù z) « (Øx Ú Øy Ú Úx) Ù (Øx Ú Øy Ú z) – КНФ,
(Øx Ú Øy Ú x) Ù (Øx Ú Øy Ú z) «(Øx Ú Øy Ú z).
Пример 3. Привести выражение 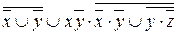 к ДНФ.
к ДНФ.
Решение:
Понижаем отрицания по правилу де Моргана. Получаем:  .
.
Пример 4.Построить СДНФ для функции 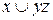 .
.
Решение:
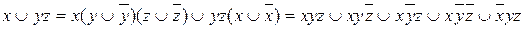 .
.
Пример 5. Построить СКНФ для функции 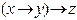 .
.
Решение:
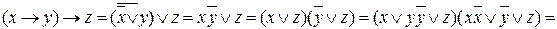
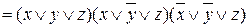 .
.
Пример 6.Привести формулу к СДНФ с помощью эквивалентных преобразований.
Решение:
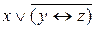
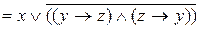
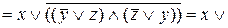
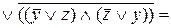
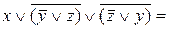

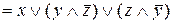 – ДНФ.
– ДНФ.
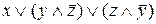 =
= 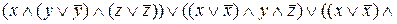
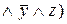 =
= 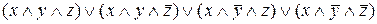
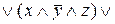
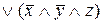 =
= 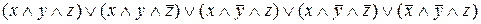 Полученная формула – СДНФ.
Полученная формула – СДНФ.
Пример 7. Привести формулу к СДНФ с помощью эквивалентных преобразований.
Решение:
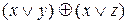 =
= 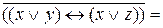

= 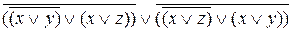 =
= 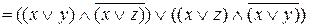 =
=
= 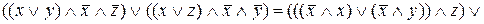
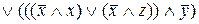 =
= 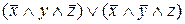 – СДНФ.
– СДНФ.
Пример 8.С помощью эквивалентных преобразований привести к ДНФ, КНФ, СДНФ, СКНФ функцию f = Ø((x Ú Øy) ® (z « Øx)).
Решение:
Приводим к ДНФ:
Ø((x Ú Øy) ® (z « Øx)) « Ø((Øx Ù y) Ú (z « Øx)) « Ø((Øx Ù y) Ú (Øz Ú Øx) Ù Ù (x Ú z)) «(x Ú Øy) Ù ((z Ù x) Ú (Øx Ù Øz) « (z Ù x) Ù (x Ú Øy) Ú (Øx Ù Øz) « « (z Ù x Ù x) Ú (z Ù x Ù Øy) Ú (Øx Ù Øz).
Приводим к СДНФ:
(z Ù x Ù x) Ú (z Ù x Ù Øy) Ú (Øx Ù Øz) « (z Ù x) Ú (z Ù x Ù Øy) Ú (Øx Ù Øz) « (zÙ Ù x) Ù (y Ú Øy) Ú (z Ù x Ù Øy) Ú (Øx Ù Øz) Ù (y Ú Øy) « (z Ù x Ù y) Ú (z Ù x Ù ÙØy)Ú (z Ù x Ù Øy) Ú (Øx Ù Øz Ù y) Ú (Øx Ù Øz Ù Øy).
Переход от ДНФ к КНФ:
Ø(Ø ((z Ù x Ù x) Ú (z Ù x Ù Øy) Ú (Øx Ù Øz))) « Ø((Øz Ú Øx Ú Øx) Ù (Øz Ú Øx Ú Úy) Ù (x Ú z)) « Ø((Øz Ú Øx) Ù (Øz Ú Øx Ú y) Ù (x Ú z)) « Ø(Øz Ú (Øx Ù Øx) Ú Ú(Øx Ù y) Ù (x Ú z)) « Ø(Øz Ú (Øx Ù Øx) Ú (Øx Ù y Ù x) Ú (Øx Ù y Ù z)) « z Ù (xÚ x) Ù (x Ú Øy Ú Øx) Ù (x Ú Øy Ú Øz).
Приводим к СКНФ:
z Ù (x Ú x) Ù (x Ú Øy Ú Øx) Ù (x Ú Øy Ú Øz) « z Ú (y Ù Øy) Ù x Ú (y Ù Øy) Ù (x Ú Ú Øy Ú Øz) « (z Ú y) Ù (z Ú Øy) Ù (x Ú y) Ù (x Ú Øy) Ù (x Ú Øy Ú Øz) « (z Ú y) Ú Ú (x Ù Øx) Ù (z Ú Øy) Ú (x Ù Øx) Ù (x Ú y) Ú (z Ù Øz) Ù (x Ú Øy Ú Øz) « (z Ú y Ú Úx) Ù (z Ú y Ú Øx) Ù (z Ú Øy Ú x) Ù (z Ú Øy Ú Øx) Ù (x Ú y Ú z) Ù (x Ú y Ú Øz) Ù (xÚ Øy Ú Øz) «(z Ú y Ú x) Ù (z Ú y Ú Øx) Ù (z Ú Øy Ú x) Ù (z Ú Øy Ú Øx) Ù (x Ú yÚ ÚØz) Ù (x Ú Øy Ú Øz).
Пример 10.Для функции f(x, y, z) = (x ~ z) | ((x y) ~ (y z))
а) составить таблицу истинности;
б) написать для нее СДНФ или СКНФ.
Решение:
а) в таблицу истинности данной функции полезно включить таблицы истинности промежуточных функций:
| xyz | x ~ z | x y | y z | (x y) ~ (y z) | (x~ z)|((x y) ~ (yz) |
б) составить СДНФ и СКНФ по полученной таблице. СДНФ составляется по единицам таблицы истинности, причем если f(x, y, z) = 1, то если х = 0, в соответствующей конъюнкции СДНФ берется 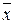 , а если х = 1 в СДНФ берется х. Аналогично поступают и с другими переменными, поэтому СДНФ для данной функции имеет вид:
, а если х = 1 в СДНФ берется х. Аналогично поступают и с другими переменными, поэтому СДНФ для данной функции имеет вид: 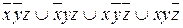 .
.
СКНФ составляется по нулям таблицы истинности, если f(x, y, z) = 0 и х = 0, то в соответствующей дизъюнкции берется х, а если х = 1, то 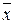 . Таким образом, СКНФ для данной функции имеет вид:
. Таким образом, СКНФ для данной функции имеет вид:
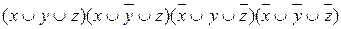 .
.
Заметим, что по определению СДНФ и СКНФ, переменные (в каждой конъюнкции и дизъюнкции соответственно) должны следовать в одинаковом порядке.
Упражнения
1. Построить СДНФ для функций:
a) f(x,y,z)=(x 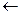 y)
y)  (y
(y  z);
z);
b) f(x,y)=(xy  1)
1)  (x
(x  z);
z);
c) f(x,y,z)=xyz 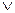 (x
(x  z)
z) 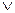 (xyz
(xyz  1);
1);
d) f(x,y,z)=(xy  z)
z)  (xz
(xz  y);
y);
e) f(x,y)=(x  y)(z
y)(z 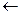 1);
1);
f) f(x,y)=(x  y)
y) 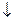 (z
(z  y);
y);
g) f(x,y)=(x  z)
z) 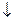 xy;
xy;
h) f(x,y,z)=(xy  z)
z) 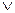 (xz
(xz 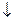 y);
y);
i) f(x,y,z)=(xy  z)
z)  (xz
(xz  y);
y);
j) f(x,y,z)=(x  z)
z) 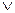 (x
(x  y)
y) 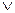 (y
(y  z);
z);
k) f(x,y,z)=(x  z)
z)  (x
(x  y).
y).
2. Построить СКНФ для функций:
a) f(x,y,z)=(x 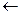 y)
y)  (y
(y  z);
z);
b) f(x,y)=(xy  1)
1)  (x
(x  z);
z);
c) f(x,y,z)=xyz 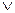 (x
(x  z)
z) 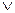 (xyz
(xyz  1);
1);
d) f(x,y,z)=(xy  z)
z)  (xz
(xz  y);
y);
e) f(x,y)=(x  y)(z
y)(z 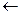 1);
1);
f) f(x,y)=(x  y)
y) 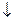 (z
(z  y);
y);
g) f(x,y)=(x  y)
y) 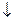 xz;
xz;
h) f(x,y,z)=(xy  z)
z) 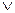 (xz
(xz 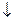 y);
y);
i) f(x,y,z)=(xy  z)
z)  (xz
(xz  y);
y);
j) f(x,y,z)=(xz 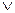 (x
(x  y))
y))  (y
(y  z);
z);
k) f(x,y,z)=(x  z)
z) 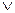 (x
(x  y)
y) 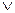 (y
(y  z).
z).
Дата добавления: 2016-04-11; просмотров: 3549;
