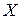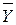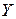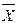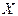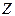Индивидуальное задание. 9. Сократить ДНФ по правилу Блейка:
9. Сократить ДНФ по правилу Блейка:
9.1 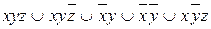 ;
;
9.2 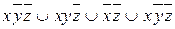 ;
;
9.3 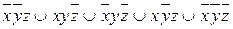 ;
;
9.4 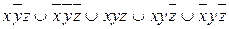 ;
;
9.5 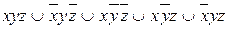 ;
;
9.6 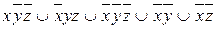 ;
;
9.7 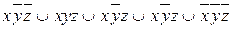 ;
;
9.8 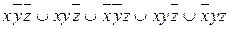 ;
;
9.9 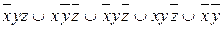 ;
;
9.10 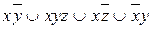 ;
;
9.11 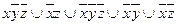 ;
;
9.12 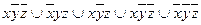 ;
;
9.13 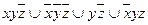 ;
;
9.14 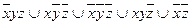 ;
;
9.15 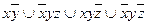 .
.
10. Составить карту Карно и найти сокращенную ДНФ для функций:
10.1 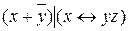 ;
;
10.2 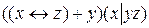 ;
;
10.3 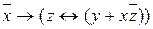 ;
;
10.4 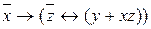 ;
;
10.5 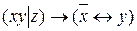 ;
;
10.6 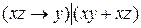 ;
;
10.7 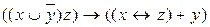 ;
;
10.8 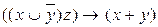 ;
;
10.9 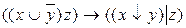 ;
;
10.10 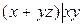 ;
;
10.11 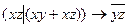 ;
;
10.12 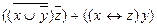 ;
;
10.13 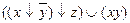 ;
;
10.14 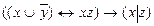 ;
;
10.15 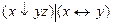 .
.
11. С помощью карт Карно по данной таблице истинности для функции четырех переменных и найти ее сокращенную ДНФ:
| 11.1 | х1, х2 | 11.2 | х1, х2 | 11.7 | х1, х2 | 11.3 | х1, х2 | |||||||||||||||||
| x3 , x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3 , x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3 , x4 | 0 0 | 0 1 | 1 1 | 1 0 | |||||
| 0 0 | 0 0 | 0 0 | 0 0 | |||||||||||||||||||||
| 0 1 | 0 1 | 0 1 | 0 1 | |||||||||||||||||||||
| 1 1 | 1 1 | 1 1 | 1 1 | |||||||||||||||||||||
| 1 0 | 1 0 | 1 0 | 1 0 | |||||||||||||||||||||
| 11.4 | х1, х2 | 11.5 | х1, х2 | 11.6 | х1, х2 | 11.7 | х1, х2 | |||||||||||||||||
| x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3 , x4 | 0 0 | 0 1 | 1 1 | 1 0 | |||||
| 0 0 | 0 0 | 0 0 | 0 0 | |||||||||||||||||||||
| 0 1 | 0 1 | 0 1 | 0 1 | |||||||||||||||||||||
| 1 1 | 1 1 | 1 1 | 1 1 | |||||||||||||||||||||
| 1 0 | 1 0 | 1 0 | ||||||||||||||||||||||
| 11.8 | х1, х2 | 11.9 | х1, х2 | 11.10 | х1, х2 | 11.11 | х1, х2 | |||||||||||||||||
| x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3 , x4 | 0 0 | 0 1 | 1 1 | 1 0 | |||||
| 0 0 | 0 0 | 0 0 | 0 0 | |||||||||||||||||||||
| 0 1 | 0 1 | 0 1 | 0 1 | |||||||||||||||||||||
| 1 1 | 1 1 | 1 1 | 1 1 | |||||||||||||||||||||
| 1 0 | 1 0 | 1 0 | ||||||||||||||||||||||
| 11.12 | х1, х2 | 11.13 | х1, х2 | 11.14 | х1, х2 | 11.15 | х1, х2 | |||||||||||||||||
| x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3, x4 | 0 0 | 0 1 | 1 1 | 1 0 | x3 , x4 | 0 0 | 0 1 | 1 1 | 1 0 | |||||
| 0 0 | 0 0 | 0 0 | 0 0 | |||||||||||||||||||||
| 0 1 | 0 1 | 0 1 | 0 1 | |||||||||||||||||||||
| 1 1 | 1 1 | 1 1 | 1 1 | |||||||||||||||||||||
| 1 0 | 1 0 | 1 0 | ||||||||||||||||||||||
Логические схемы
Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Работу логических элементов описывают с помощью таблиц истинности.
Переключательная схема – это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подается и с которых снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.
Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю – если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.
При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.
Синтез схемы сводится к следующим трем этапам:
· составление функции проводимости по таблице истинности, отражающей эти условия;
· упрощение этой функции;
· построение соответствующей схемы.
Анализ схемы сводится к:
· определению значений ее функции проводимости при всех возможных наборах входящих в эту функцию переменных;
· получению упрощенной формулы.
Простейшая схема, содержащая один переключатель P, имеет один вход 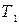 и один выход
и один выход 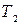 :
:
|
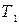
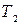
 |  |
Истинному высказыванию P = «переключатель P замкнут» поставим в соответствие переключатель P. В этом случае схема пропускает ток.
Высказыванию 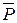 соответствует выражение «переключатель Pразомкнут», схема не проводит ток. Истина («1») интерпретируется как состояние переключателя «ток проходит», «0» (ложь) – «ток не проходит».
соответствует выражение «переключатель Pразомкнут», схема не проводит ток. Истина («1») интерпретируется как состояние переключателя «ток проходит», «0» (ложь) – «ток не проходит».
Конъюнкциидвух высказываний P&Qсоответствует схема с последовательным соединением контактов:
|
|
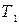
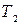
 |  |
Дизъюнкции двух высказываний P  Q соответствует схема с параллельным соединением контактов:
Q соответствует схема с параллельным соединением контактов:
 |


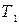
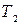
 |
Так как любая функция алгебры логики представима в виде ДНФ (или КНФ), то для любой булевой функции можно составить соответствующую схему, а каждой схеме соответствует некоторая формула алгебры логики, задающая некую булеву функцию.
Две схемы считаются эквивалентными, если через одну их них проходит ток тогда и только тогда, когда он проходит через другую. Из двух эквивалентныхсхем более простойсчитается та, которая содержит меньшее число контактов.
Пример 1. Составить РКС для следующей функции:
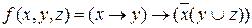 .
.
Решение:
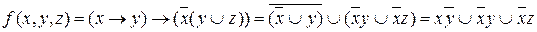 .
.
|
|
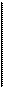

 Построим РКС:
Построим РКС:
|
|
 | |||
 |
Пример 2.Построить РКС для функции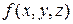 , если
, если 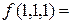
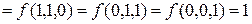 , остальные значения функции нулевые. Решение:
, остальные значения функции нулевые. Решение:
Составим СДНФ для данной функции и затем упростим:
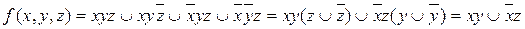 .
.
|
|
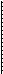

 |  | ||||
 |
Пример 3.Упростить РКС, заданную функцией 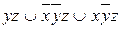 .
.
Решение:
Упростим функцию проводимости:
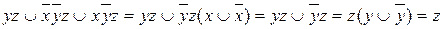 .
.
Упрощенная схема имеет вид:
|

Проблема проектирования логических схем сводится к отысканию оптимальной эквивалентной схемы, состоящей из возможно меньшего числа элементов. С математической точки зрения эта проблема сводится к задаче минимизации булевой функции, соответствующей заданной схеме. Для построения оптимальной схемы необходимо сделать следующее.
1. По заданной схеме составить соответствующую ей булеву функцию.
2. Привести эту функцию к ДНФ.
3. Минимизировать записанную в ДНФ булеву функцию одним из описанных выше способов
4. Построить релейно-контактную схему, соответствующую минимальной ДНФ.
Приведем примеры.
Пример 4.Построить оптимальную релейно-контактную схему, эквивалентную схеме.
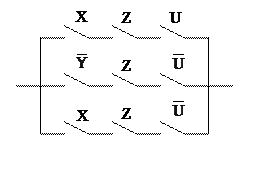
Решение:
1. Составим по этой схеме булеву функцию:
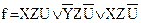 .
.
2. Эта функция записана в ДНФ, поэтому предварительных ее преобразований не требуется.
3. Склеиваем первый член с третьим:
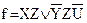 .
.
4. Строим релейно-контактную схему, соответствующую полученной функции:

В упрощенной схеме вместо 9 контактов используются только 5.
Пример 5. Построить оптимальную релейно-контактную схему, эквивалентную схеме.

Решение:
1. Заданной схеме соответствует булева функция:
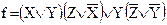 .
.
2. Представим эту функцию в ДНФ:
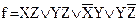 .
.
3. Склеивая второй член с четвертым, а затем проводя операцию поглощения, получим;
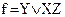 .
.
4. Строим оптимальную релейно-контактную схему (рис. 13).

Пример 6. Реализовать функцию алгебры логики 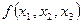 из задания 1 в виде схемы из функциональных элементов, причем выполнить реализацию, используя наименьшее число функциональных элементов.
из задания 1 в виде схемы из функциональных элементов, причем выполнить реализацию, используя наименьшее число функциональных элементов.
Решение. Для реализации функции 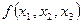 в виде схемы их функциональных элементов воспользуемся эквивалентной ей функцией
в виде схемы их функциональных элементов воспользуемся эквивалентной ей функцией
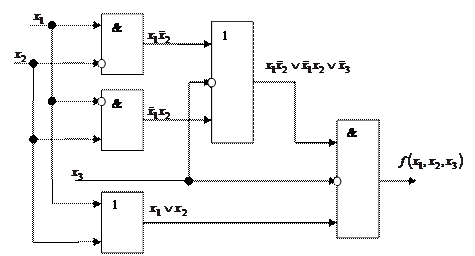
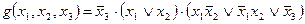 .
.
Упражнения
1. Построить схемы, реализующие следующие элементарные булевы функции:
a) 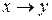 ;
;
b) 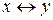 ;
;
c) 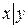 ;
;
d) 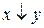 ;
;
e) 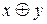 .
.
2. Реализовать схемами следующие формулы:
a) 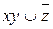 ;
;
b) 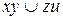 ;
;
c) 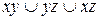 ;
;
d) 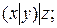
e) 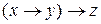 ;
;
f) 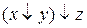 ;
;
g) 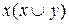 ;
;
h) 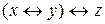 ;
;
i) 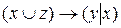 .
.
3. Из контактов p, q, r составить схему так, чтобы она замкнулась тогда и только тогда, когда замкнуты какие-нибудь два из трех контактов p, q, r.
4. Требуется, чтобы в большом зале можно было включать или выключать свет при помощи любого из четырех переключателей, расставленных на четырех стенах. Указание: это можно осуществить путем конструирования схемы, в которой свет включается, когда замкнуто четное число выключателей, и выключается свет, когда разомкнуто нечетное число выключателей.
5. Для группы из трех человек построить электрическую схему для регистрации тайного голосования простым большинством голосов. Каждый человек, голосующий «за», нажимает кнопку, «против» – не нажимает, если большинство человек голосует «за» – загорается лампочка.
Дата добавления: 2016-04-11; просмотров: 1822;