Формулы и функции алгебры логики
Высказывания, образованные из элементарных переменных высказываний путем применения операций алгебры логики, называются сложными высказываниями или формуламиалгебры логики.
Если переменным, входящим в формулу, задать определенные значения из множества 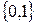 , то и формула примет определенное значение из того же самого множества, отсюда, каждая формула алгебры логики определяет некоторую свою функцию,причем и аргументы и сама функция могут принимать лишь два значения 0 или 1.
, то и формула примет определенное значение из того же самого множества, отсюда, каждая формула алгебры логики определяет некоторую свою функцию,причем и аргументы и сама функция могут принимать лишь два значения 0 или 1.
Функцию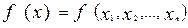 , принимающую значения 0 или 1 и определенную на всевозможных n-мерных наборах из 0 и 1, называют логической функциейили функцией алгебры логикиот n переменных.
, принимающую значения 0 или 1 и определенную на всевозможных n-мерных наборах из 0 и 1, называют логической функциейили функцией алгебры логикиот n переменных.
Любую функцию алгебры логики от n переменных можно представить с помощью таблицы истинности, в которой строки (их всего 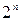 ) располагаются в порядке возрастания двоичных чисел:
) располагаются в порядке возрастания двоичных чисел:
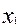
| 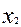
| . . . . . | 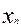
| 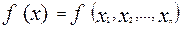
|
| . . . . . | 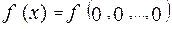
| |||
| . . . . . | 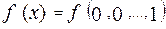
| |||
| ... | ... | . . . . . | ... | . . . . . |
| . . . . . | 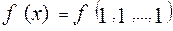
|
Числовсех функций алгебры логики от n переменных равно 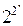 , функций алгебры логики от двух переменных – 16.
, функций алгебры логики от двух переменных – 16.
Рассмотрим эти функции:
| x | y | 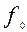
| 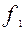
| 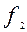
| 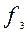
| 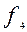
| 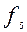
| 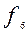
| 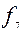
| 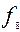
| 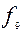
| 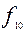
| 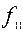
| 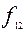
| 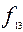
| 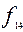
| 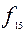
|
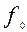 = 0 – «константа 0»;
= 0 – «константа 0»;
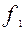 = x ∙ y–«конъюнкция» (x и y);
= x ∙ y–«конъюнкция» (x и y);
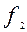 =
=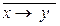 – «левая импликация»;
– «левая импликация»;
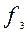 = x– «переменная x»;
= x– «переменная x»;
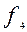 =
=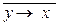 – «правая импликация»;
– «правая импликация»;
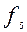 = y – «переменная y»;
= y – «переменная y»;
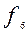 =
=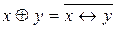 =
= 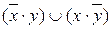 – «сложение по модулю 2»;
– «сложение по модулю 2»;
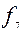 =
= 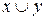 – «дизъюнкция» (x или y);
– «дизъюнкция» (x или y);
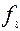 =
=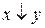 =
= 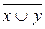 – «стрелка Пирса» (x стрелка y);
– «стрелка Пирса» (x стрелка y);
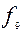 =
= 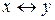 =
= 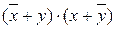 – «эквивалентноcть» (x эквивалентно y);
– «эквивалентноcть» (x эквивалентно y);
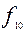 =
=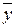 – «отрицание» (не y);
– «отрицание» (не y);
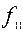 =
=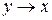 =
= 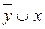 – «x правая импликация y, или y импликация x»;
– «x правая импликация y, или y импликация x»;
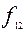 =
=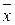 –«отрицание»(не x);
–«отрицание»(не x);
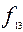 = x → y=
= x → y= 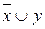 –«импликация» (если x, то y);
–«импликация» (если x, то y);
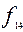 = x|y=
= x|y= 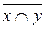 – «штрих Шеффера» (x штрих y);
– «штрих Шеффера» (x штрих y);
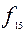 =1 – «константа 1».
=1 – «константа 1».
Для удобства записей выражений в алгебре логике в дальнейшем мы будем придерживаться следующих правил:
· если над некоторым выражением стоит отрицание, то это выражение мы не будем заключать в скобки;
· знак «&» мы будем иногда опускать (как знак операции пересечения в алгебре множеств);
· будем считать, что знак «&» сильнее, чем знаки дизъюнкции, сложения по модулю 2, эквивалентности, импликации, стрелки Пирса и штриха Шеффера, тем самым мы будем, где это возможно, опускать скобки;
· на основании закона ассоциативности мы будем опускать скобки при записи нескольких идущих подряд дизъюнкций и конъюнкций.
Согласно определению таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то наборов значений переменных восемь: (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Если при всех наборах значений переменных x и y формула принимает значение 1, то является тождественно истинной, если при всех наборах значений переменных x и y формула принимает значение 0, то является тождественно ложной, если формула в некоторых случаях принимает значение 1, а в некоторых – 0, то есть является выполнимой.
Булевы функции могут быть заданы либо с помощью таблиц истинности (единственным образом), либо с помощью логических формул (неединственным образом). Если таблицы истинности двух булевых формул совпадают, то эти формулы эквивалентны и определяют одну и ту же булеву функцию.
Пример 1.Проверить эквивалентность булевых формул 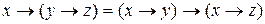 .
.
Решение:
Построим таблицу истинности для функции 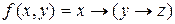 .
.
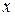
| 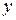
| 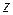
| 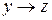
| 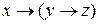
|
Построим таблицу истинности для функции 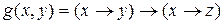 .
.
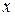
| 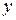
| 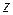
| 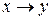
| 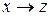
| 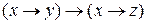
|
Результирующие столбцы в таблицах истинности совпадают, следовательно, формулы эквивалентны.
Пример 2. Проверить, будут ли эквивалентны следующие формулы:
xÙ (y ® z) и (x Ù y) ® (x Ù z).
Решение:
| x | y | z | y ® z | x Ù (y ® z) | x Ù y | x Ù z | (x Ù y) ® (x Ù z) |
Таблицы истинности не совпадают, следовательно, формулы не эквивалентны.
Пример 3.Проверить, будут ли эквивалентны следующие формулы: 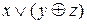 и
и 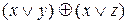 .
.
Решение:
| x | y | z | 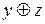
| 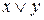
| 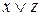
| 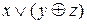
| 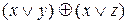
|
Дата добавления: 2016-04-11; просмотров: 1412;
