Индивидуальное задание. 1. Установите, какие из предложений являются логическими высказываниями, а какие – нет (объясните почему)
1. Установите, какие из предложений являются логическими высказываниями, а какие – нет (объясните почему), сформулируйте отрицания:
1.1 «Солнце есть спутник Земли»;
1.2 «2+3=4»;
1.3 «Сегодня отличная погода»;
1.4 «В романе Л. Н. Толстого “Война и мир” 3 432 536 слов»;
1.5 «Санкт-Петербург расположен на Неве»;
1.6 «Музыка Баха слишком сложна»;
1.7 «Первая космическая скорость равна 7.8 км/сек»;
1.8 «Железо – металл»;
1.9«Если один угол в треугольнике прямой, то треугольник будет тупоугольным»;
1.10 «Иван Петров плотник»;
1.11«Студент учатся в институте»;
1.12«Треугольник – плоская геометрическая фигура, состоящая из трех углов и трех сторон»;
1.13«Каждый квадрат есть ромб»;
1.14«Курица не птица»;
1.15«Математика – это наука».
2.Запишите предложение формулой логики высказываний, постройте к нему отрицание:
2.1 Неверно, что Иванов и Петров оба не выдержали экзамена.
2.2 Если Коля умен, а Вася нет, то Коля получит аттестат с отличием.
2.3 Если в классе идут занятия, то на улице хорошая погода.
2.4 Валя ходит в кино только в том случае, когда там показывают комедию.
2.5 Треугольники подобны, если они равны.
2.6 Противоположные стороны параллелограмма равны и параллельны, в противном случае четырехугольник не параллелограмм, а трапеция.
2.7Неверно, что у ромба все углы острые и диагонали не перпендикулярны.
2.8 Или Катя пойдет в кино, а Сергей не пойдет, или они оба пойдут в школу.
2.9 Если курс ценных бумаг растет или процентная ставка снижается, то либо падает курс акций, либо налоги не повышаются.
2.10 Либо четырехугольник - квадрат, либо прямоугольник, если все углы у него прямые.
2.11«Сумма цифр числа 216 делится на 3, значит само число 216 делится на 3, так как существует соответствующее правило»;
2.12«Треугольник, в котором все стороны равны, равносторонний, если две стороны равны - равнобедренный»;
2.13«Я понимаю, что не понимаю математическую логику, поэтому мне необходимо дополнительно заниматься дома»;
2.14«Если Иван Иванович Иванов не будет ходить на работу, то он или не получит зарплату, или будет уволен»;
2.15«Максим учится в школе, и делает уроки старательно, это значит, что он отличник».
Таблицы истинности
Истинность высказывания можно установить с помощью таблицы истинности. Таблица истинности – это таблица, состоящая из нулей и единиц и устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции.
Таблицы истинности применяются для:
· вычисления истинности сложных высказываний;
· установления эквивалентности высказываний;
· определения тавтологий.
1. Таблица истинности инверсии:
| A | 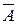
|
2. Таблица истинности дизъюнкции:
| A | B | А 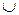 В В
|
3. Таблица истинности конъюнкции:
| A | B | А ∙ В |
4. Таблица истинности импликации:
| А | В | А→ В |
5. Таблица истинности эквиваленции:
| А | В | А↔ В |
6. Таблица истинности строгой дизъюнкции:
| А | В | А+В |
Высказывание «Eсли я куплю яблоки или абрикосы, то приготовлю фруктовый пирог» формализуется в виде 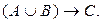 Такая же формула соответствует высказыванию «Если Игорь знает английский или японский язык, то он получит место переводчика».
Такая же формула соответствует высказыванию «Если Игорь знает английский или японский язык, то он получит место переводчика».
Формула 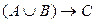 при определенных сочетаниях значений переменных A, B и C принимает значение «истина», а при некоторых других сочетаниях – значение «ложь». Такие формулы называются выполнимыми.
при определенных сочетаниях значений переменных A, B и C принимает значение «истина», а при некоторых других сочетаниях – значение «ложь». Такие формулы называются выполнимыми.
Некоторые формулы принимают значение «истина» при любых значениях истинности входящих в них переменных и называются тождественно истинными формулами или тавтологиями.
Высказывание «Катя самая высокая девочка в классе, и в классе есть девочки выше Кати» формализуется в виде: 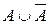 . Очевидно, что эта формула ложна, так как либо
. Очевидно, что эта формула ложна, так как либо 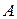 , либо
, либо 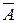 обязательно ложно.
обязательно ложно.
Такие формулы называются тождественно ложными формулами или противоречиями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом «=» или « 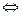 ». Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
». Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Пример 1.Установить истинность высказывания 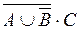 .
.
Решение:
В состав сложного высказывания входят простые: А, В, С. В таблице заполняются колонки значениями (0, 1). Указываются все возможные ситуации. При составлении таблицы надо следить за тем, чтобы не перепутать порядок действий; заполняя столбцы, следует двигаться от элементарных формул к более сложным; столбец, заполняемый последним, содержит значения исходной формулы.
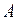
| 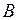
| 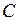
| 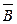
| 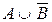
| 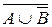
| 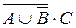
|
Из таблицы видно, что данное высказывание истинно только в случае, когда А=0, В=1, С=1. Во всех остальных случаях оно ложно.
С помощью таблиц истинности можно установить эквивалентность двух или нескольких высказываний.
Высказывания называются эквивалентными, если соответствующие значения каждого из них совпадают в таблице истинности.
Пример 2. Проверить эквивалентность высказываний 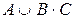 и
и 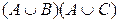 .
.
Решение:
Проверка ведется путем составления таблицы истинности:
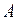
| 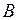
| 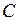
| 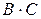
| 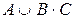
| 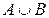
| 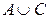
| 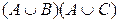
|
Сравнивая 5-ю и 8-ю колонки, убеждаемся, что все значения, получаемые по формуле 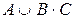 , совпадают со значениями, получаемыми по формуле
, совпадают со значениями, получаемыми по формуле 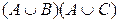 , т. е. высказывания эквивалентны (равносильны). Одно может заменить другое.
, т. е. высказывания эквивалентны (равносильны). Одно может заменить другое.
Эквивалентные (равносильные) высказывания соединяют знаком «↔» («≡», «~», « 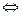 »). Отметим различие между эквивалентностью и эквиваленцией. Эквиваленция является логической операцией, позволяющей по двум заданным высказываниям А и В построить новое. Эквивалентность же является отношением между двумя составными высказываниями, состоящим в том, что их значения истинности всегда одни и те же.
»). Отметим различие между эквивалентностью и эквиваленцией. Эквиваленция является логической операцией, позволяющей по двум заданным высказываниям А и В построить новое. Эквивалентность же является отношением между двумя составными высказываниями, состоящим в том, что их значения истинности всегда одни и те же.
Пример 3. Докажите тавтологию 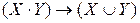 .
.
Решение:
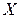
| 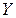
| 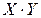
| 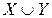
| 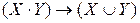
|
Так как высказывание всегда истинно, то оно является тавтологией.
Пример 4. Докажите тавтологию ((X→Y)→(Y→Z))→(X→Z).
Решение:
_ _ _ _ _ _ _ _ _ _ _ _ _ F1 _ _ _ _ F2 _ _ _ _ _ F3
| X | Y | Z | X→Y | Y→Z | X→Z | F1→F2 | (F1→F2) →F3 |
Из таблицы видно, что исследуемое высказывание – тавтология, так как оно тождественно истинно.
Упражнения
1.Установить, какому из высказываний эквивалентно высказывание 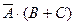 :
:
а) 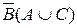 ; б)
; б) 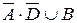 ; в)
; в) 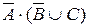 ; г)
; г) 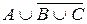 .
.
2. Установить с помощью таблиц истинности, какие из следующих формул являются тавтологиями:
а) 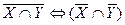 ; б)
; б) 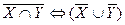 ; в)
; в) 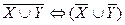 ;
;
г) 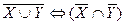 .
.
3. Установить истинность высказывания 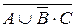 .
.
4. Проверить эквивалентность высказываний 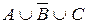 и
и 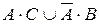 .
.
5. Установить, являются ли высказывания тавтологиями:
а) 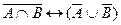 ; б)
; б) 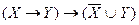 .
.
6. Для каждой формулы придумайте формализуемые ими предложения:
а) 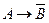 ; б)
; б) 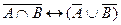 ; в)
; в) 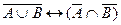 .
.
7. Из простых высказываний: «Виктор хороший пловец» – А, «Виктор хорошо ныряет» – В, «Виктор хорошо поет» – С, составлено сложное высказывание 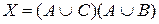 . Установить, эквивалентно ли составленное высказывание
. Установить, эквивалентно ли составленное высказывание 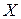 следующему: «Виктор – хороший пловец и певец».
следующему: «Виктор – хороший пловец и певец».
8. Установить истинность высказываний:
а) 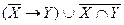 ;
;
б) 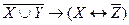 .
.
9. Установить истинность высказываний:
а) 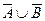 ,
, 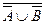 ,
, 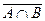 ;
;
б) 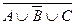 ,
, 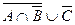 ,
, 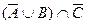 ;
;
в) 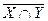 ,
, 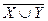 ,
, 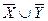 .
.
г) 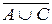 ,
, 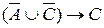 .
.
Дата добавления: 2016-04-11; просмотров: 2683;
