Основные теоремы теории вероятности.
Суммой двух событий А и В называется событие С, состоящее в появлении или события А или события В, или обоих событий вместе.
С=А 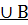
Произведением двух событий А и В называется событие С, состоящее в том, что произойдет и событие А и событие В.
С=А 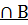
Событие В называется независимым от события А, если появления события А не изменяет вероятности появления события В, в противном случае событие А и В являются зависимыми.
Теорема умножения вероятностей независимых событий.
Вероятность совместного появления двух или нескольких независимых событий равна произведению вероятностей этих событий.
Р(А 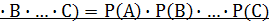
Пример 1 найти вероятность совместного выхода в финал чемпионата России по футболу команд «Спартак» и «Локомотив», если вероятность выхода в финал команды «Спартак» (событие А) равна 0,7, а команды «Локомотив» (событие В) равна 0,9.
Решение. Событие А и В независимые, поэтому по теореме умножения, искомая вероятность
Р(АВ)=Р(А) 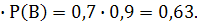
Теорема умножения вероятностей зависимых событий.
Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляют в предположение, что все предыдущие события уже наступили.
Р(А 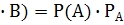 (В) ,
(В) ,
где 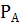 (В)- вероятность события В, вычисленная в предположении, что событие А уже наступило.
(В)- вероятность события В, вычисленная в предположении, что событие А уже наступило.
Пример 2. В школьной команде по легкой атлетике тренируются 5 юношей из 10 «а» и 6 юношей из 10 «б» классов. При отборе в финал городских соревнований сначала был отобран один спортсмен, а затем другой. Найти вероятность того, что первым был отобран ученик 10 «а» класса, а вторым - ученик 10 «б» класса.
Решение. Вероятность того, что первым спортсменом окажется ученик 10 «а» (событие А) Р(А)= 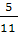 .
.
Вероятность того, что вторым спортсменом окажется ученик 10 «б» (событие В), вычисляется в предположении, что первый спортсмен – ученик 10 «а», т. е. условная вероятность 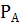 (В)=
(В)= 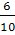 .
.
По теореме умножения искомая вероятность
Р(А 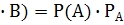 (В)=
(В)= 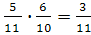 .
.
Дата добавления: 2016-03-10; просмотров: 746;
