Числовые характеристики ДСВ и их свойства.
Очень часто вместо закона распределения ДСВ приходиться использовать для описания случайной величины ее числовые характеристики, к которым относятся математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическое ожидание ДСВ называют сумму произведений ее возможных значений на их вероятности:
М(x)=  +
+ 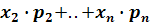 =
= 
Вероятностный смысл математического ожидания заключается в том, что оно приближенно равно наиболее ожидаемому в результате испытания значению случайной величины.
Свойства математического ожидания
1.М (С)=С
2.М (СХ)=СМ (Х)
3.М ( 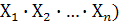 =М (
=М (  …
… 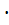 М(
М( 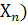
4. М ( 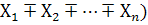 =М (
=М ( 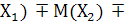 …
… 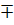 М(
М( 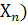
5. М ( 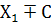 )=М (
)=М (  )
) 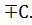
Математическое ожиданиебиномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:
М (Х)=np.
Рассеяние случайной величины около среднего значения характеризуют дисперсия и среднее квадратичное отклонение.
Дисперсией ДСВ называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X ) = 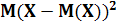
Для практических вычислений пользуются следующей формулой:
D(X) = 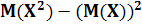 ,где М(x)=
,где М(x)= 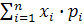
Свойства дисперсии.
1. D(C)=C
2. D(CX)= 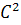 D(X)
D(X)
3. D(X+Y+Z)=D(X)+D(Y)+D(Z)
4. D(X-Y)=D(X)+D(Y)
Пример 2. Случайные величины X и Y независимы. Найти математическое ожидание и дисперсию случайной величины Z=3X-2Y,если известно, что М(Х)=0,3, М(Y)=-1,5 D(X)=5, D(Y)=6.
Решение.
М(Z)=M(3X-2Y)=M(3X)-M(2Y)=3M(X)-2M(Y)=3  ,3+2
,3+2 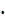 (-1,5)=-2,1
(-1,5)=-2,1
D(Z)=D(3X-2Y)=D(3X)+D(2Y)=9D(X)+4D(Y)=9 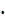 5+4
5+4 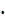 6=69
6=69
Дисперсия биномиального закона распределения равна произведению числа испытаний на вероятности появления события в одном испытании:
D(X)=npq
Пример 3 .Найти математическое ожидание и дисперсию случайной величины Х-числа появления события А в 20 независимых испытаниях, если вероятность появления события А в каждом испытании равна 0,78.
Решение. Случайная величина Х распределена биномиально.
n=20; p=0,78; q=1-p=1-0,78=0,22
М (Х)=np=20 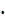 0,78=15,6;
0,78=15,6;
D(X)=npq=20 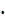 0,78
0,78 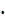 0,22=3,432
0,22=3,432
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения помимо дисперсии служит среднее квадратическое отклонение.
Средним квадратическим отклонением величины Х называют квадратный корень из дисперсии:

Пример 4.Найти числовые характеристики ДСВ Х, заданной законом распределения:
| Х | -5 | |||
| Р | 0,4 | 0,3 | 0,1 | 0,2 |
Решение.
М(Х)=-5 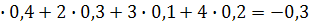
D(X)=M( 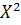 )-
)- 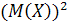
M( 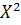 )=
)=  15,3
15,3
D(X)= 15,3- 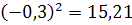
 =
= 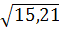 =3,9.
=3,9.
Дата добавления: 2016-03-10; просмотров: 3170;
