Сравнение двух выборочных средних. t-критерий Стьюдента.

При сравнении данных двух выборок на основании расчета t-критерия Стьюдента группы могут различаться:

1.по объему входящих в них данных:

а) обе группы большие (n>30);

б) обе группы малые (n<30);

в) одна- большая (n>30), другая малая (n<30).

2.по своему составу:

а) группы с зависимыми вариантами, когда i-тая варианта первой группы сравнивается с i-той вариантой второй группы (сравнение результатов повторных тестирований одной и той же выборки, n_x=n_y );

б) группы с независимыми вариантами (можно менять варианты местами внутри выборки, т. е. данные тестирования по одному и тому же показателю у разных групп).

При применении методов сравнения, основанных на расчете t-критерия, необходимо производить расчет числа степеней свободы.

Под числом степеней свободы понимают разность между числом измеряемых (наблюдаемых) значений и числом линейных отношений (связей ), возникающих между ними.

Для критерия Стьюдента расчет степеней свободы производится по формуле: К=n_x+n_y-2, где n_x-объем выборки X, где n_y- объем выборки Y.

При сравнение двух больших или одной большой и одной малой групп с независимыми вариантами применяют формулу:

,

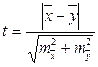где 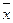, 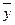- величины средних выборок Х и Y;

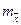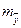, - стандартные ошибки средних выборок Х и Y.

Сравнение двух малых групп с независимыми вариантами проводится по формуле:

.

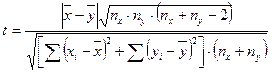Сравнение двух малых групп с зависимыми вариантами проводится по формуле: ,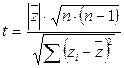

где 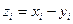; ; 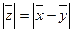n - число испытуемых

Расчет степеней свободы в данном случае, т. к. n_x=n_y, проводиться по формуле: К=2·(n-1).

После того как произведен расчет t- критерия Стьюдента и числа степеней свободы, из таблицы t- критерия Стьюдента находится критическое значение t- критерия для трех порогов доверительной вероятности β и уровней значимости α. Если t_ф<t_st (минимального значения из таблицы), то между данными двух выборок не наблюдается достоверности различий, то есть они примерно равные по данному показателю, и, следовательно, предположение о различиях в показателях выборок оказывается ошибочным. Если же t_ф> t_st, то говорят о достоверности различий при определенной доверительной степени доверительной вероятности.