Первичная обработка выборочных данных
Получение выборочных данных
1.1.1 Выбираются
· Объект исследования - генеральная совокупность с объёмом N (числом элементов, которое может считаться и бесконечным);
· Исследуемая величина Х, количественный признак каждого элемента совокупности;
· Единица совокупности как наименьший неделимый элемент, для которого свойственен данный признак;
· Уровень достоверности  для полученных результатов;
для полученных результатов;
1.1.2 Совокупность подвергается сплошному обследованию для получений значения признака для каждого её элемента. Если сплошное обследование очень трудоёмко или невозможно, то следует из генеральной совокупности взять часть её элементов – выборочную совокупность. По уровню достоверности находится наименьший объём выборки n, обеспечивающий такую достоверность;
1.1.3 Выбирается способ отбора элементов выборочной совокупности из генеральной совокупности. При этом должна быть обеспечена репрезентативность выборки т.е. сохранение в ней закономерностей, свойственных генеральной совокупности;
1.1.4 Производится отбор n элементов из генеральной совокупности в соответствии с выбранным способом. После обследования каждого выбранного элемента получим значения  , которые называют выборкой. Если признак является качественным т.е. полученные значения не являются числовыми, то следует перейти к числовым (например, пронумеровав его возможные значения);
, которые называют выборкой. Если признак является качественным т.е. полученные значения не являются числовыми, то следует перейти к числовым (например, пронумеровав его возможные значения);
Первичная обработка выборочных данных
1.2.1 После расположения значений  по возрастанию (убыванию) составляется ранжированный ряд;
по возрастанию (убыванию) составляется ранжированный ряд;
1.2.2 Составляется статистическое распределение выборки
· Если среди значений имеются повторяющиеся, то составляется вариационный ряд (дискретное распределение выборки), где каждому из различных значений  ставится в соответствие его частота
ставится в соответствие его частота 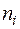 т.е. количество наблюдений такой варианты в данной выборке. Иногда находится также относительная частота, доля
т.е. количество наблюдений такой варианты в данной выборке. Иногда находится также относительная частота, доля 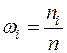 иногда
иногда 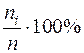 . При этом
. При этом 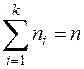 ,
, 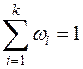 ,
,  ;
;
· При интервальном распределении признака задаются промежутки изменений для Х и находится частота 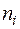 или относительная частота
или относительная частота  наблюдений значений в данном промежутке;
наблюдений значений в данном промежутке;
1.2.3 Распределение выборки изображается графически
· По вариационному ряду (дискретному распределению выборки) строится полигон распределения – ломаная с вершинами  ;
;
· По интервальному распределению строится гистограмма частот как множество к прямоугольников с параллельными координатным осям сторонами, основанием каждого является промежуток  и высота равна частоте
и высота равна частоте 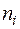 наблюдений значений в таком промежутке. Аналогично строится гистограмма относительных частот, когда высоту прямоугольника берут равной
наблюдений значений в таком промежутке. Аналогично строится гистограмма относительных частот, когда высоту прямоугольника берут равной  ;
;
· При интервальном распределении выборки составляется выборочная плотность распределения  , которая на каждом промежутке
, которая на каждом промежутке  имеет значение
имеет значение 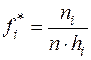 при
при  ;
;
· Выборочная функция распределения 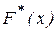 в точке х равна сумме относительных частот для значений переменной меньше данного х;
в точке х равна сумме относительных частот для значений переменной меньше данного х;
· Можно использовать также различные виды диаграмм картограмм и т.д. Круговая диаграмма изображается кругом, разбитым на сектора. Доля каждого сектора в площади круга берется равной относительной частоте соответствующей варианты или промежутка значений для признака в объёме выборки;
1.2.4 Находятся числовые характеристики выборки 
1.2.4.1 Выборочное среднее 
· Для несгруппированных данных  ;
;
· По вариационному ряду  ;
;
· По интервальному распределению  ,
,
где  - середина промежутка с номером
- середина промежутка с номером 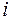 ;
;
1.2.4.2 Выборочная дисперсия 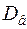
· Для несгруппированных данных 
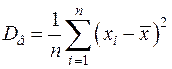 ,
,
другой способ вычисления 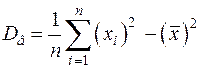 ;
;
· По вариационному ряду
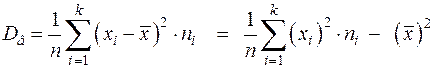
· По интервальному распределению
 ;
;
1.2.4.3 Исправленная дисперсия 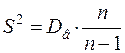 ;
;
1.2.4.4 Среднеквадратичное (стандартное) отклонение 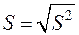 ;
;
1.2.4.5 При необходимости находятся 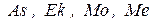 , V:
, V:
· Коэффициент вариации  ;
;
· Коэффициент асимметрии  ;
;
· Коэффициент эксцесса  ;
;
· Мода  , медиана
, медиана 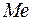 и т.д.
и т.д.
·
и производится анализ полученных результатов;
Дата добавления: 2016-04-11; просмотров: 1478;
