Нормальное распределение.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

f(x)=

Т. е. нормальное распределение определяется двумя параметрами: α и δ. Достаточно знать эти параметры , чтобы задать нормальное распределение.

Вероятностный смысл этих параметров таков: α- математическое ожидание, δ – среднее квадратичесное отклонение.

Общим называют распределение с произвольным параметрами α и δ ( δ>0).

Нормированным или стандартным называют нормальное распределение с параметрами α= 0 и δ=1

Плотность стандартного распределения имеет вид:

График плотности нормального распределения называют нормальной кривой (кривой Гаусса)

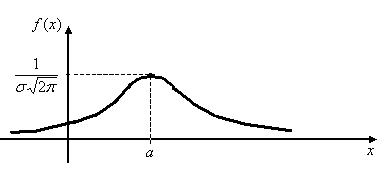
Вероятность того, что непрерывная случайная величина Х, распределенная нормально, примет значение из интервала (а;b) равна

P(a )

Пример 5. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 12. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12,14).

Решение. Воспользуемся формулой. Подставив a=12, b=14, α= 10 и δ=2, получим

P(12 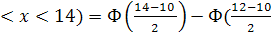)=Ф(2)-Ф(1).

По таблице приложения находим Ф(2)=0,4772 и Ф(1)= 0,3413. Искомая вероятность Р(12<Х<14)=0,4772-0,3413=0,1359.

Правило тех сигм

Если случайная величина распределена нормально , то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т. е.

Р(|Х- α |<3 δ)=0,9973≈1

На практике это правило применяет так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле выполняется, то есть основание предполагать, что изучаемая случайная величина распределена нормально; в противном случае она не распределена нормально.