Многомерное нормальное распределение

1.6 Многие статистические методы разработаны в предположении, что распределение рассматриваемого признака имеет нормальную форму. Это обусловлено рядом причин. Во-первых, допущение в своем приближенном виде часто реализуется на практике. Распределения многих скелетных размеров тела у взрослых мужчин и женщин хорошо соответствуют этому типу кривой. Асимметричность распределений многих других антропометрических признаков может быть устранена применением, например, логнормальной трансформации вида Y =

= lg (X + X_o), где X_o вычисляется так, что распределение Y оказывается максимально близким к нормальному виду. Во-вторых, допущение нормальности позволяет разработать разнообразный статистический инструментарий. Наконец, использование модели нормального распределения позволяет значительно уменьшить количество показателей, описывающих свойства изменчивости отдельно взятого признака. Действительно, если изучаемый признак X имеет нормальное распределение, то его дифференциальная функция имеет вид

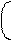
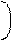1 X_i – M ²

-

1 2 s

f(X_i) = e , (1.11)

s (2p)^1/2

где X_i - значение признака, являющееся аргументом функции, M и s - его средняя арифметическая величина и среднее квадратическое отклонение, p и e - математические константы. Нетрудно видеть, что в формулу (1.11) входят только два параметра – M и s.

1.7. Обобщением одномерного нормального распределения служит его мно-гомерная форма. Если дан набор m признаков с индивидуальным вектором наблюдений

X_i' = X_1i X_2i X_3i ... X_mi ,

то дифференциальная функция многомерного нормального распределения имеет вид

₁

1 - ¾ (X_i - M)' S^-1(X_i - M)

f(X_i) = e ²

(2p)^{m / 2} (ôSô)^1/2 (1.12)

где X_i - вектор индивидуальных наблюдений, являющийся аргументом функции, M - вектор средних, S - ковариационная матрица, p и e - математические константы. Нетрудно видеть, что формулы (1.11) и (1.12) - весьма схожи.

В степени числа e в первом случае находится квадрат нормированной формы значения признака, которую можно переписать в виде (X - M) (s² )^-1(X - M), во

- 10 -

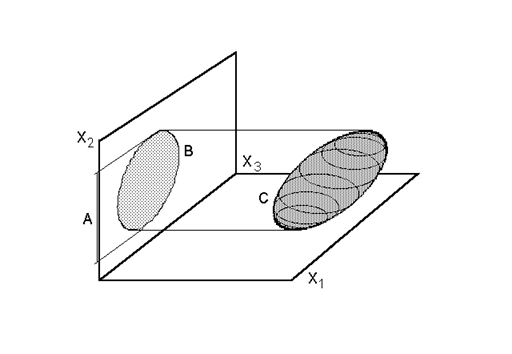
Рисунок 1.2. Области значений одного признака (А), сочетаний двух (В) и трех признаков (С), содержащие некоторую долю всех наблюдений

втором - (X_i - M)' S^-1(X_i - M) . В многомерном случае значение признака X_i заменено вектором наблюдений X_i, средняя величина M - вектором средних M,дисперсия s² - ковариационной матрицей S. В знаменателе отношения перед числом e в первом случае находится s - среднее квадратическое отклонение (корень квадратный из дисперсии), в многомерной ситуации - (ôSô)^1/2 - корень квадратный из обобщенной дисперсии. Разность (X_i - M), стоящая в показателе степени числа e в формуле (1.12), является вектором

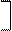
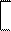
(X_i - M)' = (X_1i – M₁) (X_2i - M₂) (X_3i – M₃) ... (X_mi - M_m) ,

состоящим из отклонений значений отдельных признаков от своих средних арифметических величин. Как можно видеть из раздела А.12. Приложения А, выражение (X_i - M)' S^-1(X_i - M) есть скалярная величина, и проблем с вычислением степени числа e не возникает.

1.8 Знание закона распределения некоторого признака позволяет определять количество наблюдений, попадающих в некоторый числовой интервал его значений. Например, в случае одномерного нормального распределения интервал с границами M -1.96s и M + 1.96s включает примерно 95% всех наблюдений в какой-нибудь многочисленной выборке. Иными словами, область изменчивости одного признака, содержащая некоторую долю всех его значений, геометрически может быть изображена отрезком на числовой оси, вдоль которой он измерен (рис.1.2 А).

- 11 -

Аналогичным образом, по сочетанию двух признаков X₁ и X₂ область плоскости, образованной их осями, которая включает определенную долю всех наблюдений, может быть ограничена так называемым корреляционным эллипсом (рис.1.2 В). Его форма, зависящая от соотношения двух его осей, будет определяться величинами дисперсий двух признаков s₁² и s₂² и величиной коэффициента корреляции r между ними. Размещение центральной точки корреляционного эллипса на плоскости двух признаков будет зависеть только от средних величин M₁ и M₂. Этот эллипс образуется множеством точек плоскости, для координат X_1i и X_2i , каждой из которых выражение

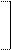
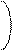
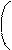
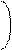
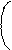
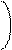
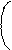
1 X_1i-M₁ ² X_2i-M₂ ² X_1i-M₁ X_2i-M₂

C² = + - 2r

1 - r² s₁ s₂ s₁ s₂

характеризуется постоянством своей величины. Легко проверить, что это выражение есть частный двумерный случай для показателя степени (X_i - M)' S^-1(X_i - M), но выписанный в обычном алгебраическом виде. Показатель C² связан с соответствующей ему долей P всех наблюдений, находящихся внутри корреляционного эллипса, соотношением

- c²/2

P = 1 - e .

В ситуации трех признаков, X₁, X₂ и X₃ область трехмерного пространства, образованного их осями, которая включает определенную долю всех наблюдений, окажется ограниченной так называемым трехмерным корреляционным эллипсоидом (рис.1.2 С). Соотношения трех его осей, а следовательно и его форма - будут определяться дисперсиями (s₁², s₂², s₃²) и коэффициентами корреляции (r₁₂, r ₁₃, r ₂₃) трех признаков. Координатами его центральной точки в трехмерном пространстве, будут являться средние величины M₁, M₂ и M₃.

Наконец, в общем случае m признаков X₁, X₂, X₃, …, X_m индивидуальные наблюдения разместятся в m-мерном пространстве их осей, которое невозможно изобразить графически. Область, включающая определенную долю P всех наблюдений, будет ограничена m-мерным корреляционным эллипсоидом. Соотношения его m осей определятся структурой ковариационной матрицы S набора признаков, а расположение его центра в m-мерном пространстве, связанном с осями этих m признаков, будет задано вектором средних M.

1.9 Точно так же, как в двумерном случае, многомерный корреляционный эллипсоид может считаться образованным множеством точек m-мерного пространства для наборов координат X₁, X₂, X₃, …, X_m . Для каждой из этих точек будет наблюдаться одна и та же величина дифференциальной функции многомерного нормального распределения (1.12). Это в свою очередь влечет за собой условие размещения точек m-мерного пространства на одном корреляционном эллипсоиде

(X_i - M)' S^-1(X_i - M) = const . (1.13)

Иными словами, все векторы индивидуальных наблюдений, для которых будет соблюдаться условие (1.13), окажутся размещенными на некотором корреляционном

- 12 -

эллипсоиде, включающем определенную долю P всех случаев. Эта доля может быть легко определена, так как выражение

c² = (X_i - M)' S^-1(X_i - M) (1.14)

имеет распределение c² c числом степеней свободы n равным m - числу признаков. В этом случае с использованием таблиц этого распределения или применением соответствующих компьютерных программ можно легко определить какая доля P всего распределения c² оказывается левее вычисленной по формуле (1.14) величины. Именно P наблюдений оказываются внутри корреляционного эллипсоида, определяемого условием (1.13).

Величина (X_i - M)' S^-1(X_i - M) = D² называется расстоянием Махаланобиса индивидуального вектора наблюдений X_i от центральной точки многомерного корреляционного эллипсоида. Варьируя D² и соответствующее ему значение доли P, можно получить семейство корреляционных эллипсоидов, различающихся по количеству размещающихся внутри них наблюдений. Например, пусть имеется набор 20 признаков. Тогда по таблицам распределения c² для числа степеней свободы n = m = 20 можно найти, что корреляционный эллипсоид, включающий P = = 0.5 всех наблюдений, характеризуется уровнем расстояния Махаланобиса до центральной точки равным 19.3. Для эллипсоида, включающего P = 0.95 всех индивидуальных случаев, D² = 31.4, при P = 0.99 - D² = 37.6 и при P = 0.999 - D² =

= 45.3.

1.10. Описанные в предыдущем разделе свойства многомерных корреляционных эллипсоидов могут использоваться в практике биометрических исследований. Если исследователю известны многомерные характеристики некоторой группы населения - вектор средних M и ковариационная матрица S, то можно определить с какой вероятностью P любое встретившееся наблюдение с вектором значений признаков X относится к этой группе. Для определения такого P достаточно по формуле (1.14) вычислить значения расстояния Махаланобиса D², после чего для распределения c² с учетом количества признаков как числа степеней свободы n следует найти P как площадь под кривой этого распределения, лежащую левее величины D².

Подобного рода задача может возникать в следующих ситуациях. Во-первых, некоторые наблюдения могут показаться "выбросами", т.е. содержащими либо ошибочные значения признаков, либо относящимися к крайне девиантным индивидам. Положив условием типичности уровень вероятности P = 0.999, можно определить для него предельную величину расстояния Махаланобиса D² . Например, для 20 признаков D_о²= 45.3. Тогда любое наблюдение, для которого D² > D_о², может считаться "выбросом" и не включаться в дальнейший анализ вместе с остальными более типичными наблюдениями.

Следует заметить, что описанная методика рассмотрения "выбросов" является по существу обобщением широко известного в одномерной статистике правила "трех сигм". Оно основано на том, что внутри числового интервала с границами M - 3s и M + 3s содержится P = 0.997 всех наблюдений нормально распределенного

- 13 -

признака. Многомерная методика, опирающаяся на вычисление расстояния Махаланобиса для корреляционных эллипсоидов позволяет решать такую же задачу для набора нормально распределенных признаков.

Во-вторых, использование корреляционных эллипсоидов может решать те же самые задачи, которые рассматривались с применением двумерных эллипсов, примером чего могут быть исследования эндокранов ископаемых гоминид, проведенные В.И.Кочетковой (1973). Здесь для получения зоны сочетаний значений двух признаков, включающей 50% случаев, характерных для современных людей, строился соответствующий корреляционный эллипс, и на его фоне рассматривались размеры эндокранов различных форм ископаемых гоминид. Свойства многомерных корреляционных эллипсоидов позволяют решать аналогичные задачи при исследованиях в области эволюционной антропологии, но с использованием уже не двух, а - практически любого числа признаков черепа, костей посткраниального скелета, эндокрана и любых иных показателей, для которых наблюдается нормальная форма распределения.

Следует, конечно, помнить о том, что описанная методика использования многомерных корреляционных эллипсоидов может применяться в случае, когда распределение признаков действительно оказывается нормальным. В ситуациях, когда это условие выполняется приблизительно, все найденные с применением этой методики результаты будут также всего лишь приближенными.