Линейные комбинации признаков

1.11 Во многих методах многомерной статистики используется понятие линей-ной комбинации признаков. Пусть мы рассматриваем набор признаков X₁, X₂, X₃, …, X_m и пусть вектор индивидуальных наблюдений для i-го случая равен

X_j' = X _1j X _2j X _3j …X _mj .

Пусть также имеется вектор некоторых коэффициентов c

c'= c ₁ c ₂ c ₃ … c _m .

Тогда для любого индивида можно вычислить скалярное произведение

y_j= c'X_j =c ₁X _1j + c ₂X _2j + c ₃X _3j + … + c _{mX mj} , (1.15)

которое называется линейной комбинацией вектора X. Она может быть найдена для любого индивида, если для него известен вектор наблюдений X_i. По существу y_j может трактоваться как некий новый признак, к которому мы переходим от набора исходных показателей, измеряемых непосредственно. Однако, при соответствующем выборе или, что встречается чаще - специальном вычислении, коэффициентов c_i, линейная комбинация y_j может иметь наперед заданные оптимальные свойства, которыми исходные признаки не обладают.

Определим основные свойства нового признака, находимого как линейная комбинация исходных показателей. Если для последних в некоторой совокупнос-

- 14 -

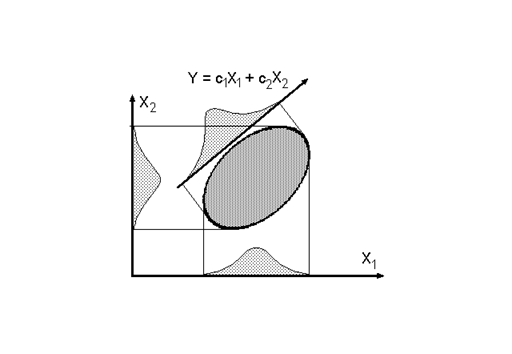
Рисунок 1.3. Иллюстрация понятия линейной комбинации исходных признаков

Y = c₁X₁ + c₂X₂

сти индивидов характерно многомерное нормальное распределение с вектором средних M и ковариационной матрицей S, то линейная комбинация y = c'X будет

иметь одномерное нормальное распределение со средней

M_y= c'M =c ₁M _1j + c ₂M _2j + c ₃M _3j + … + c _{mM mj} (1.16)

и с дисперсией

s_y² = c' S c (1.17)

1.12. Проиллюстрируем понятие линейной комбинации набора признаков геометрически. Совокупность m признаков образует m-мерное пространство, в котором в виде точек с координатами, соответствующими значениям этих признаков, изображаются индивидуальные наблюдения. Эти точки образуют облако, которое может быть заключено в некоторый корреляционный эллипсоид. Двумерный случай изображен на рисунке 1.3. Если нам задан набор коэффициентов c, соответствующий линейной комбинации y = c' X, то его элементы c ₁ c ₂ c ₃ … c _m зададут в пространстве признаков координатную ось y, по которой можно будет измерять

значения этого нового признака у всех индивидов. Эти элементы определят, в частности, углы наклона новой оси по отношению к осям X₁ и X₂. Если спроецировать все точки корреляционного эллипса на ось признака X₁, можно получить одномерное распределение этого показателя. Точно также проекции всех точек, соответствующих наблюдениям, на оси X₂ дадут распределение этого признака. Аналогично, проекции всех наблюдений на новую ось y определят распределение

- 15 -

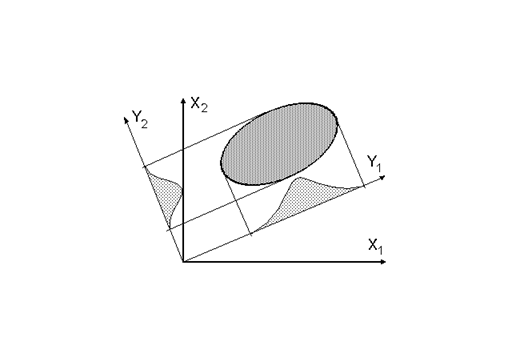
Рисунок 1.4. Иллюстрация перехода от набора исходных признаков X₁ и X₂ к системе двух новых переменных, находимых как линейные комбинации исходных признаков y₁ = c₁₁X₁ + c₂₁X₂ и y₂ = c₁₂X₁ + c₂₂X₂

значений этого нового показателя со средней арифметической M_y = c'M, и дисперсией s_y² = c' S c и нормальной формой кривой распределения.

1.13 Пусть теперь для набора m признаков X ₁, X ₂ ,X ₃ , … ,X_m нам необходимо получить как линейную комбинацию не один новый признак y = c'X, а целое их семейство, включающее n новых показателей y ₁, y ₂ ,y ₃ , … ,y_n . Пусть первый из их y₁ = c₁'Xнаходится при помощи набора коэффициентов c₁' = [c₁₁ c ₂₁ c₃₁ c _m1], второй - y₂ = c₂'X - при помощи c₂' = [c₁₂ c ₂₂ c₃₂ c _m2], и т.д., последний - y_n =c_n'X по вектору c_n' = [c_1n c _2n c_3n c _mn]. Тогда из n векторов-строк c_i' можно получить единую матрицу

c'₁ c₁₁ c₂₁ c₃₁ … c_m1

c'₂ c₁₂ c ₂₂ c₃₂ … c_m2

C= c'₃ = c₁₃ c₂₃ c ₃₃ … c_m3 ,

… … … … … …

c’_N c_1n c_2n c_3n … c_mn

а переход от m исходных признаков к n новым переменным - записать в компакт-ном виде y' = C'X , где y' - набор новых признаков

y' = [y₁ y₂ y₃ … y_n] .

- 16 -

Новые признаки y₁, y₂, y₃, …, y_nмогут иметь такие желательные свойства, которых обычно лишены исходные показатели X₁, X₂, X ₃, …, X_m , но которые не- обходимы тем или иным причинам.

Для набора новых переменных y вектор средних M_y может быть найден как

M_y = С'M , (1.18)

а ковариационная матрица S_y- в виде

S_y = C'SC , (1.19)

где M и S - вектор средних и ковариационная матрица набора исходных признаков X₁, X₂, … , X_m . Формулы (1.18) и (1.19) являются обобщением (1.16) и (1.17).

В частности, ковариация для любой пары новых переменных y_i = c_i'Xи y_j = c_j'X (при i ¹ j) может быть получена по формуле

cov_ij = c_i'Sc_j, (1.20)

а коэффициент корреляции - из

cov_ij c_i'Sc_j

r_ij = = . (1.21)

s_y1 s_y2 (c_i'Sc _i c_j'Sc_j)^1/2

Очень часто новые признаки получаются как нескоррелированные показатели, так что для всех сочетаний i и j cov_ij = c_i'Sc_j= 0. В этом случае

s_y1² 0 0 … 0

0 s_y2² 0 … 0

S_y = 0 0 s_y3² … 0 .

… … … … …

0 0 0 … s_ym²

1.14. Геометрически переход от набора m исходных признаков X к системе n новых переменных y, находимых как линейные комбинации y = C'X, означает переход к новой системе координат (рис.1.4), в которой для y₁, y₂, y₃, ..., y_n будет наблюдаться нормальное распределение, если для набора X также была характерна нормальность. Количество новых линейных комбинаций (n) может быть мень-шим числа исходных признаков (m). Тогда для набора y можно получить не только желаемые оптимальные свойства, но также добиться уменьшения (иногда - весьма значительного) количества анализируемых переменных. Это может сделать получаемые результаты более компактными и имеющими большие возможности содержательной интерпретации.