Глава 1. Описание набора признаков

МНОГОМЕРНЫЕ АНАЛОГИ ОДНОМЕРНЫХ СТАТИСТИЧЕСКИХ

МЕТОДОВ

Глава 1. Описание набора признаков

1.1 В одномерной биометрии рассматривалась ситуация изучения вариации одного отдельно взятого признака. Его величина у некоторого j-го индивида X_j была скаляром. Вся выборка таких значений у N индивидов с учетом матричных обозначений может считаться некоторым вектором. Пусть теперь мы имеем не один, а m признаков, рассматриваемых как нечто единое. Пусть этот набор показателей измерен у некоторого j-го индивида. Тогда этот набор индивидуальных значений признаков может быть записан в виде вектора-строки, имеющего длину соответствующую числу признаков m

X_j' = X _1j X _2j X _3j …X _mj . (1.1)

Такой вектор называется вектором индивидуальных наблюдений. Его реальным аналогом является антропологический бланк, на котором в определенной последовательности записаны значения всех изучаемых показателей у некоторого человека. Вектор наблюдений является многомерным аналогом отдельного наблюдения по какому-то признаку.

При исследовании некоторой выборки N индивидов мы будем иметь дело с N векторами индивидуальных наблюдений, из которых как из строк одинаковой длины можно составить прямоугольную матрицу

X'₁ X₁₁ X₁₂ X₁₃ …X_1m

X'₂ X₂₁ X₂₂ X₂₃ …X_2m

X= X'₃ = X₃₁ X₃₂ X₃₃ …X_3m , (1.2)

… … … … … …

X’_N X_N1 X_N2 X_N3 …X_Nm

которая называется матрицей данных. Ее строками являются индивидуальные векторы наблюдений, а каждый столбец включает значения некоторого признака у всех N индивидов. Поэтому, она имеет размер m * N. Аналогом таблицы данных является электронная таблица с введенными в нее значениями признаков. Возможность формирования таких таблиц содержится в большинстве компьютерных статистических пакетов программ.

В одномерной биометрии для выборки N индивидуальных значений отдельного признака использовалось получение компактного описания, которое включало небольшую батарею показателей, таких как средняя арифметическая величина, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса и др.

- 5 -

По их значениям можно было сделать суждение о центральном уровне значений признака, его изменчивости, форме кривой его распределения.

Пусть теперь нам необходимо получить сходное описание для набора признаков X₁, X₂, X ₃, …, X _m. Для каждого i-го показателя мы можем вычислить среднюю арифметическую величину

N

M_i = ∑ X_ij

N ^{j = 1}

где N - объем выборки, i = 1, 2, 3, ..., m и j = 1, 2, 3, ..., N. Из совокупности средних арифметических величин для всех признаков можно составить вектор

M' = M ₁ M ₂ M ₃ …M _m , (1.3)

который называется вектором средних и содержит всю необходимую информацию для суждения о размещении центров распределений всех признаков на числовых осях измерения их величины.

К понятию вектора средних можно придти иначе. Поступая с векторами индивидуальных наблюдений X_j как с отдельными значениями признака, когда необходимо получить его среднюю величину, можно найти вектор средних по обычной формуле

N

M= ∑ X_j

N ^{j = 1}

где j = 1, 2, 3, ..., N. Таким образом, вектор средних может рассматриваться как средняя арифметическая величина для векторов индивидуальных наблюдений. Он оказывается естественным многомерным аналогом средней арифметической величины по какому-то признаку.

1.3. В качестве показателя вариации каждого из m признаков можно вычислить дисперсию

1 _N

s_i² = ∑ (X_ij - M_i)²,

N – 1 ^{j = 1}

где N - объем выборки, i = 1, 2, 3, ..., m, и j = 1, 2, 3, ..., N. В одномерной статистике используется также корень квадратный из нее s_i - среднее квадратическое отклонение.

В качестве показателя соотносительной изменчивости любых двух i-го и k-го признаков может быть использована их ковариация

1 _N

cov_ik = ∑ (X_ij - M_i)(X_kj - M_k) .

N – 1 ^{j = 1}

Нетрудно видеть, что дисперсия и ковариация являются сходными показателями, описывающими изменчивость. Это становится еще более очевидным, если основу дисперсии – сумму квадратов отклонений наблюдений от средней -

- 6-

∑(X_ij - M_i)² переписать в ином виде - ∑(X_ij - M_i)(X_ij - M_i) . Тогда можно видеть, что дисперсия является своего рода ковариацией признака с самим собой. Это позволяет свести дисперсии m признаков и ковариации всех их попарных сочетаний в единую матрицу. Для достижения стандартного обозначения ее элементов можно воспользоваться символом s_ii для дисперсии i-го признака и s_ik- для ковариации i-го и k-го признака. Тогда такая матрица может быть записана в виде

s₁₁ s₁₂ s₁₃ … s_1m

s₁₂ s₂₂ s₂₃ … s_2m

S = s₁₃ s₂₃ s₃₃ …s_3m . (1.4)

… … … … …

s_1m s_2m s_3m … s_mm

Она называется ковариационной матрицей набора m признаков. Эта матрица - симметрическая, так как любой внедиагональный элемент s_ik, являющийся ковариацией i-го и k-го признаков, равен s_ki - ковариации k-го и i-го признаков. На главной диагонали находятся дисперсии всех отдельных m признаков - s₁₁, s₁₂, s₃₃,_. …s_mm. Ковариационная матрица является многомерным аналогом обычной дисперсии и включает все показатели изменчивости, которые можно найти для набора признаков.

Для любого признака можно перейти к нормированной его z-форме в соответствии с формулой

X_ij - M_i

z_ij = ,

s_i

где X_ij - исходное значение i-го признака у j-го индивида, M_i - средняя арифметическая величина и s_i - среднее квадратическое отклонение i-го признака. Для нормированных значений z_ij характерно то, что они выражены в относительных неименованных величинах, имеют среднюю арифметическую величину, равную нулю, и среднее квадратическое отклонение, равное единице.

Для нормированных величин признаков ковариация превращается в коэффициент корреляции, так как его формула предполагает

cov_ik

r_ik =

s_i s_i

а средние квадратические отклонения нормированной формы i-го и k-го признаков равны единице (s_i = 1 и s_k = 1).

Для нормированного набора признаков, составляющего векторы индивидуальных наблюдений,

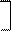
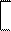
z_j' = z _1j z _2j z _3j … z _mj . (1.5)

вектор средних включает нули

- 7 -

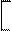
M_z' = 0 0 0 … 0 . (1.6)

В силу того, что для нормированного набора признаков дисперсии равны единице, а ковариации равны коэффициентам корреляции, ковариационная матрица приобретает специальный вид

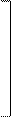r₁₁ r₁₂ r₁₃ … r_1m

r₁₂ r₂₂ r₂₃ … r_2m

R = r₁₃ r₂₃ r₃₃ …r_3m , (1.7)

… … … … …

r_1m r_2m r_3m … r_mm

называемый корреляционной матрицей.

1.5. Ковариационная матрица S, являясь многомерным аналогом дисперсии отдельно взятого признака, в ряде случаев все же не вполне удобна для использования, так как не позволяет оценить интегративную величину вариации набора признаков одним скалярным числовым показателем. Для такой цели часто используется ее определитель │S│, который называется обобщенной дисперсией набора признаков. Наглядно пояснить смысл такого показателя удобнее на примере простейшего набора двух признаков X₁ и X₂.

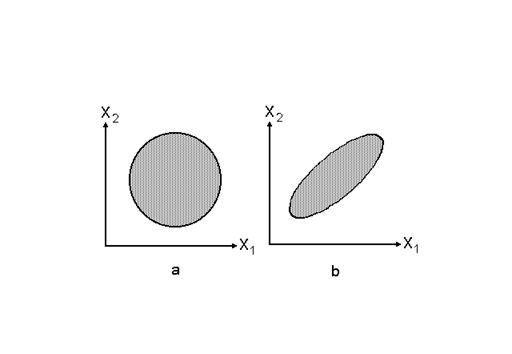
Рисунок 1.1. К определению обобщенной дисперсии двух признаков X₁ и X₂ при их взаимной некоррелированности (a) и в случае ненулевой тесноты связи (b)

- 8 -

В этом случае ковариационная матрица имеет вид

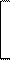
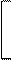
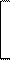s₁₁ s₁₂ s₁² cov₁₂ s₁² s₁s₂r

S = = =

s₁₂ s₂₂ cov₁₂ s₂² s₁s₂r s₂²

где s₁ и s₂- средние квадратические отклонения признаков, а r - коэффициент корреляции между ними. Определитель этой ковариационной матрицы или обобщенная дисперсия набора двух признаков X₁ и X₂ равен

│S│ = s₁₁s₂₂ - s₁₂s₁₂ = s₁²s₂²(1 - r²) . (1.8)

Рассмотрим его свойства. Пусть два признака нескоррелированы (r = 0). Тогда обобщенная дисперсия

│S│ = s₁²s₂² (1.9)

равна произведению дисперсий двух признаков. Она будет тем больше, чем больше окажется суммарная величина показателей вариации каждого из двух признаков. Интуитивно этот результат вполне ясен.

В ситуации, когда между двумя признаками наблюдается ненулевая корреляция, эту статистическую связь можно описать при помощи прямолинейной регрессии

X₂ = a_o + a₁X₁.

В этом случае изменчивость признака X₁ будет измеряться дисперсией s₁², тогда как с учетом наличия регрессионной связи остаточную вариацию признака X₂ опишет частная дисперсия

s_o2² = s₂²(1 - r²) .

Обобщенная дисперсия двух скоррелированных признаков может быть представлена в виде

│S│ = s₁² s_о2² , 1.10)

то есть как произведение двух дисперсий, описывающих два независимых компонента вариации. Ясно, что в ситуации коррелированности двух признаков их обобщенная дисперсия уменьшается тем сильнее, чем выше корреляция. При максимальной тесноте корреляционной связи (r = 1) обобщенная дисперсия становится равной нулю │S│ = 0.

Сказанное можно представить графически (рис.1.1) для признаков с равными дисперсиями. Ситуации r = 0 соответствует корреляционный эллипс, являющийся кругом. При появлении связи и по мере ее увеличения этот эллипс приобретает все более вытянутую форму. При этом его площадь сокращается и соответственно уменьшается разброс точек, соответствующих отдельным наблюдениям. Этому явно соответствует и уменьшение обобщенной дисперсии. В предельном случае, когда r = 1, все возможные значения X₁ и X₂ размещаются на линии регрессии, и никакой вариации наблюдений около нее не существует. В этой ситуации, естественно, обобщенная дисперсия становится нулевой.

Следует заметить, что существует рекомендация Л.А.Животовского (1984) в качестве обобщенной дисперсии использовать не определитель ковариационной матрицы │S│, а применять значения корня степени m из него (│S│)^{1/ m}, где m - число признаков в наборе. Такой показатель не зависит от числа признаков.

- 9 -