Показатели положения.
а) Выборочная средняя (средняя арифметическая).
Выборочным средним называется такое значение признака, сумма отклонений от которого выборочных значений признака равна нулю (с учетом знака отклонения).
Для несгруппированных данных выборочное среднее рассчитывается как частное от деления суммы всех значений вариант рассматриваемой совокупности на их число:
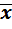 =
=  или
или 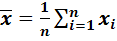 ,
,
где 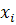 -варианты выборки;
-варианты выборки; 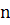 - объем выборки;
- объем выборки; 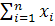 -сумма n чисел
-сумма n чисел 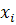 , где индекс i=
, где индекс i= 
Если данные сгруппированы, то
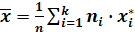 ,
,
где-n-объем выборки; k-число интервалов; 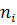 -частоты интервалов;
-частоты интервалов; 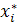 -среднее значение интервалов.
-среднее значение интервалов.
Выборочное среднее для сгруппированных данных называют также взвешенным средним, подчеркивая этим, что 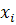 суммируются с коэффициентами (весами), равными частотами попадания в интервалы группировки.
суммируются с коэффициентами (весами), равными частотами попадания в интервалы группировки.
Свойства выборочного среднего.
1. Если все варианты ряда уменьшить (увеличить) на одно и то же число, то среднее арифметическое уменьшится (увеличится) на то же число.
2. Если все варианты ряда уменьшить (увеличить) в одно и то же число раз, то среднее арифметическое уменьшится (увеличится) во столько же.
3. Сумма отклонений вариант ряда от выборочной средней равна нулю
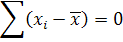
Пример 2. Найти выборочную среднюю в пр.1
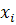 , см ~ 260; 255; 240; 250; 250; 264; 250; 262; 252; 258. (n=10)
, см ~ 260; 255; 240; 250; 250; 264; 250; 262; 252; 258. (n=10)
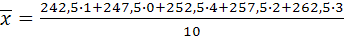 =255,5
=255,5
б) Медиана.
Медианой (Ме)-называется такое значение признака Х, когда одна половина значений экспериментальных данных меньше ее, а вторая половина- больше.
1) Если число данных n в выборке нечетно, то медиане соответствует ранг:
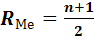
Например:n=9
8; 12; 12; 14; 16; 18; 20; 22; 22.
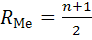 =
= 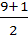 =5, следовательно, Ме=16
=5, следовательно, Ме=16
2) Если число данных n в выборке четно, то медиана выбирается равной среднему арифметическому из двух значений, занимающих в этом месте по порядку
Например : n=10
6; 10; 11; 12; 12; 14; 18; 19; 20; 20.
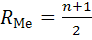 =
= 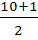 =5,5 , следовательно, Ме=
=5,5 , следовательно, Ме=  =13,5.
=13,5.
3)В интервальном вариационном ряду вначале определяют медианный интервал.
Медианным будет тот интервал, в котором накопленная частота впервые окажется больше  (n – объем выборки)
(n – объем выборки)
Внутри медианного интервала медиана определяется по формуле:
Ме= 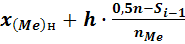 ,
,
где - 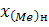 -нижняя граница медианного интервала;
-нижняя граница медианного интервала; 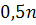 - половина объема выборки;
- половина объема выборки; 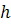 - ширина интервалов группировки;
- ширина интервалов группировки; 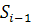 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному; 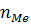 - частота медианного интервала.
- частота медианного интервала.
Пример 3. По сгруппированным данным пр.1найти медиану.
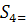 7
7 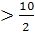 ,следовательно, медианный интервал (255-260)
,следовательно, медианный интервал (255-260)
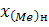 =255;
=255;  =
= 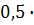 10=5 ;
10=5 ; 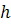 =5;
=5; 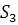 =5;
=5; 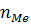 =2
=2
Ме = 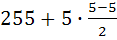 = 255.
= 255.
в) Мода(Мо) представляет собой значении признака, встречающееся в выборке наиболее часто.
8; 12; 12; 12; 14; 16; 18; 20; 22. Мо=12.
Интервал группировки с наибольшей частотой называется модальным.
В интервальном вариационном ряду мода определяется по формуле:
Мо= 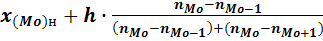
где-  - нижняя граница модального класса;
- нижняя граница модального класса; 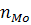 - частота модального класса;
- частота модального класса; 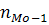 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;  -частота интервала, последующего модальному;
-частота интервала, последующего модальному; 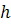 - ширина интервалов группировки.
- ширина интервалов группировки.
Пример 4. По сгруппированным данным пр.1найти моду.
Модальный интервал (250-255), т.к. 
 =250;
=250; 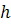 =5;
=5; 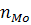 =4;
=4; 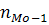 =0;
=0;  =2
=2
Мо=  =250+5
=250+5 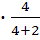 =253,3
=253,3
3.2 Показатели рассеяния (вариации)
Простейшим показателем вариации является вариационный размах R, равный разности между наибольшим и наименьшим значением ряда:
R= 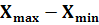
Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их средней арифметической.
Эта числовая характеристика служит для того, чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее средней арифметической.
Дисперсия, вычисляемая по выборочным данным, называется выборочной дисперсией.
Выборочную дисперсию вычисляют по формулам:
1) Для несгруппированых данных:
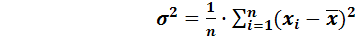 ,
,
где  - сумма квадратов отклонений значений признака
- сумма квадратов отклонений значений признака 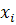 от среднего арифметического
от среднего арифметического 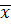 ; n-объем выборки.
; n-объем выборки.
2) Для сгруппированых данных в интервальном вариационном ряду:
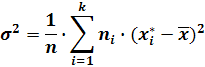
где 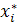 -среднее значение интервалов группировки;
-среднее значение интервалов группировки; 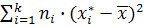
взвешенная сумма квадратов.
На практики используют формулы:
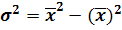
где для несгруппированных данных :
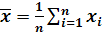

где для сгруппированных данных :
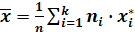 ,
, 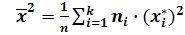 .
.
Пример 5.
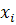
| 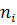
| 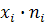
| 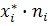
|
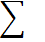
|
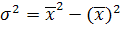 =
=  =253,19-240,25=12,94
=253,19-240,25=12,94
Свойства дисперсии.
1.Если все значения вариант уменьшить на постоянную величину, то дисперсия не изменится.
2. Если все значения вариант увеличить (уменьшить) в С раз, то дисперсия увеличится (уменьшится) в  раз.
раз.
Стандартное отклонение – вариационного ряда есть арифметическое значение корня квадратного из дисперсии
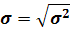
При сопоставлении (или сравнении) разноименных признаков вводится относительный показатель, называемый коэффициентом вариации или коэффициентом изменчивости признака, который вычисляется по формуле:
V= 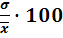 %
%
Коэффициент вариации является относительной мерой рассеивания признака.
Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку.
№5. Лекция. Статистическое исследование зависимостей. Корреляционный анализ и регрессионный анализ.
1.Статистические гипотезы и их виды.
2.Корреляционный анализ и регрессионный анализ.
Дата добавления: 2016-03-10; просмотров: 3368;
