Абсолютные показатели вариации и способы их расчета

Для характеристики абсолютной колеблемости признака используются размах вариации, среднее линейное отклонение, дисперсия, среднеквадратическое отклонение.

Размах вариации представляет собой разность между максимальным и минимальным значением признака:

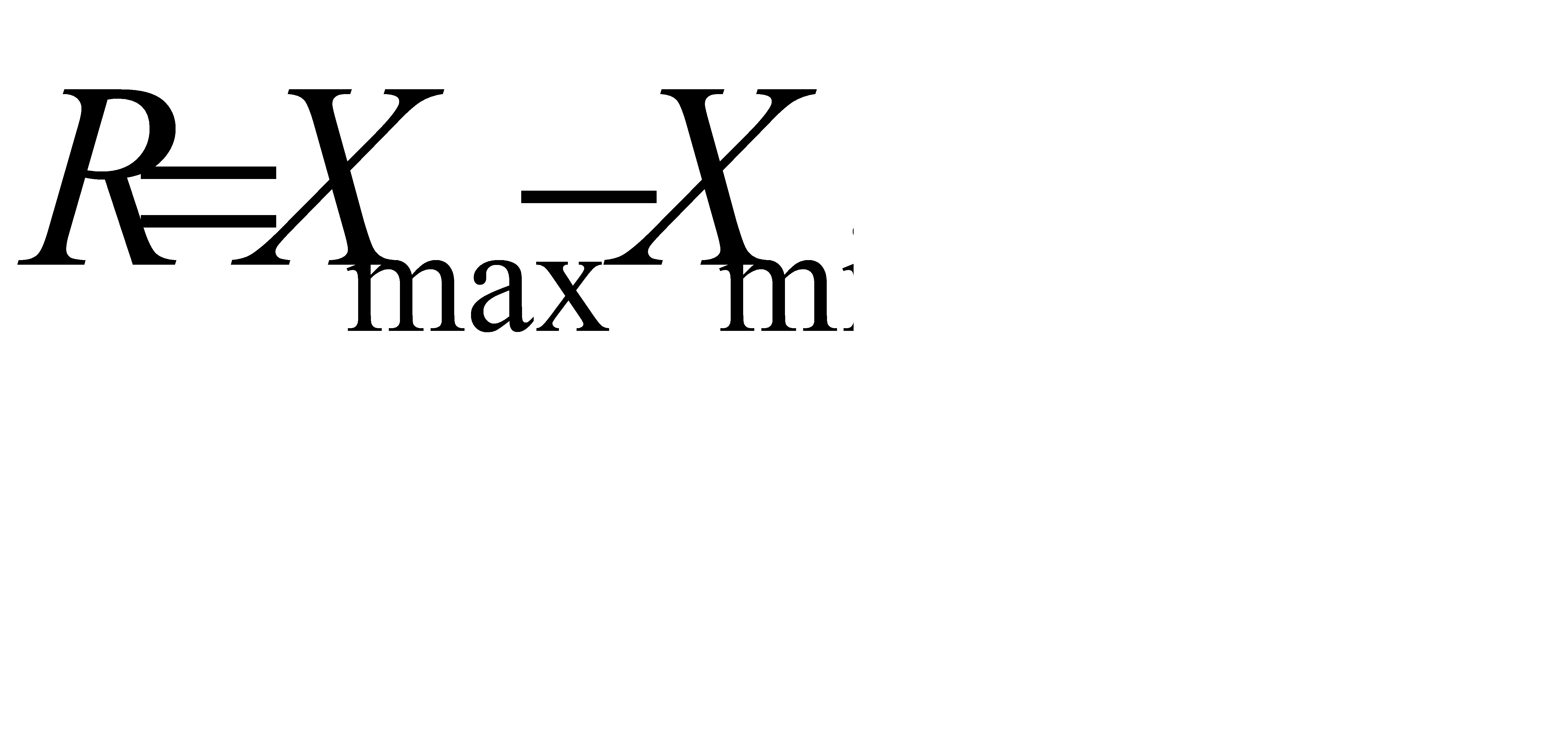(5.3)

Достоинством этого показателя является простота расчета. Однако размах вариации зависит только от крайних значений признака, не учитываются частоты и отсутствует связь со средней величиной, поэтому область его применения ограничена однородными совокупностями.

Среднее линейное отклонение дает обобщающую характеристику распределению отклонений и учитывает различие всех единиц изучаемой совокупности. Среднее линейное отклонение определяется как средняя арифметическая из абсолютных значений отклонений индивидуальных значений от средней.

При расчете этого показателя по несгруппированным данным используется формула:

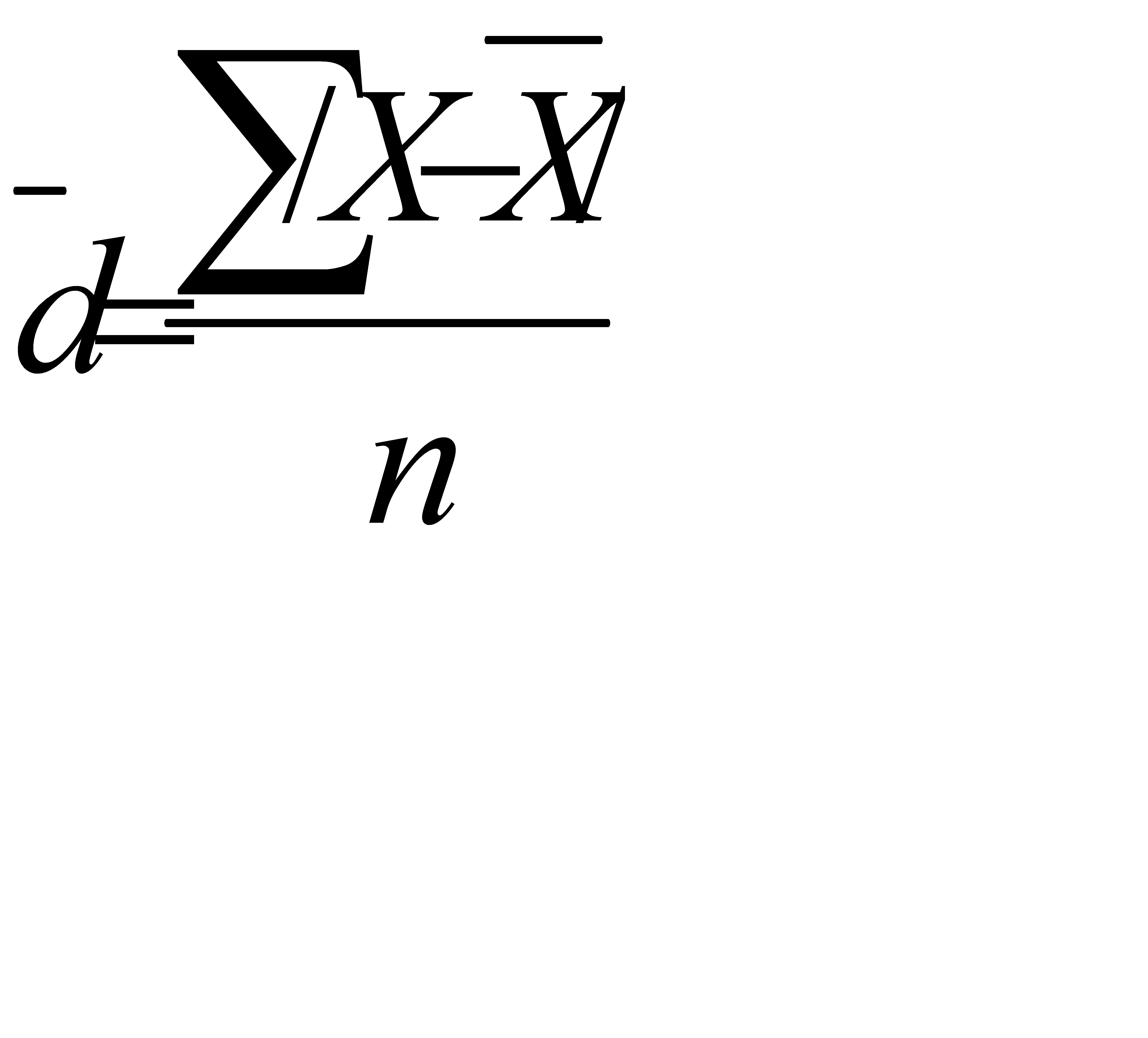(5.4)

При расчете по сгруппированным данным определяется взвешенное линейное отклонение:

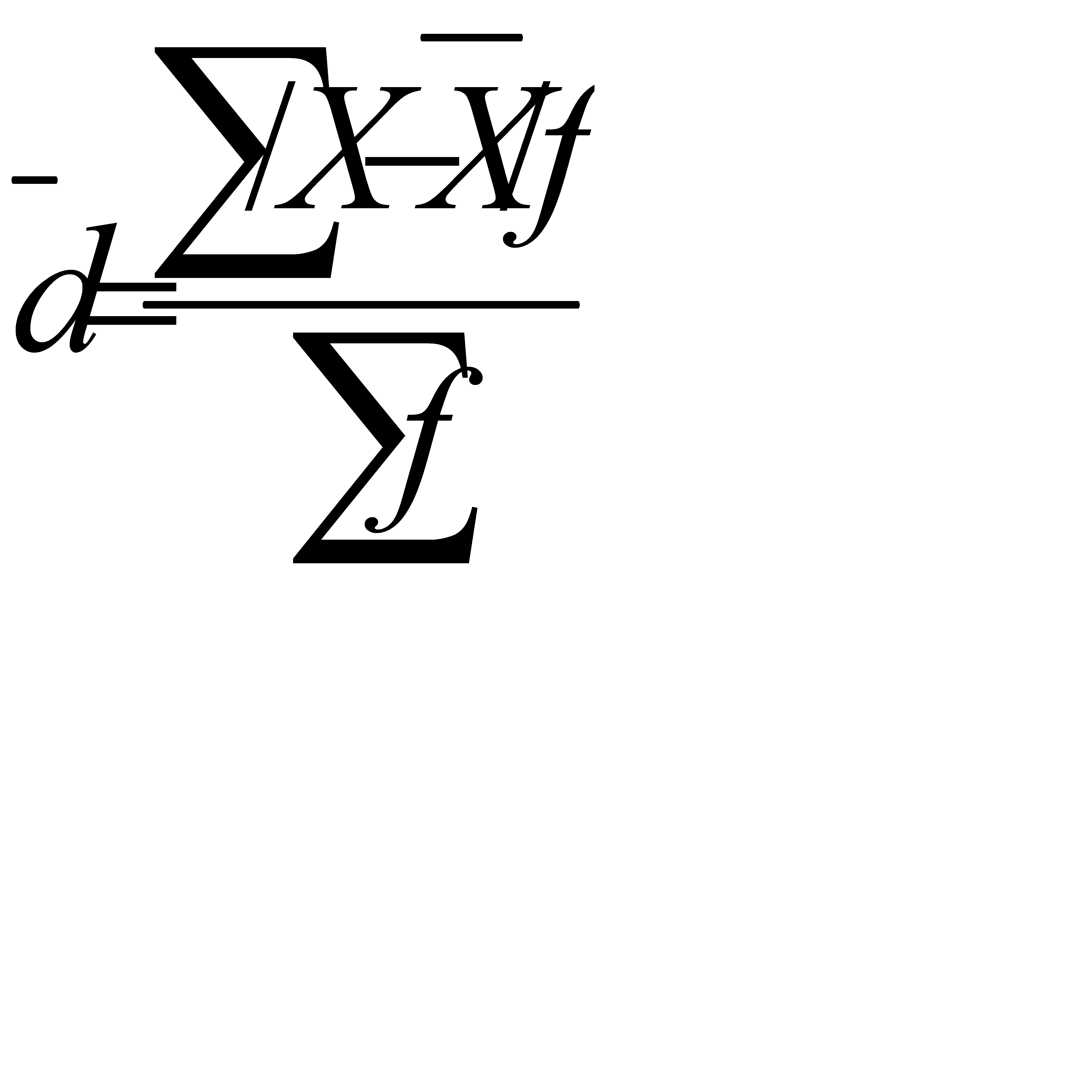(5.5)

Дисперсия и среднеквадратическое отклонение - наиболее широко применяемые на практике показатели вариации.

Дисперсия определяется как средний квадрат отклонений вариантов от их средней величины:

для несгруппированных данных:

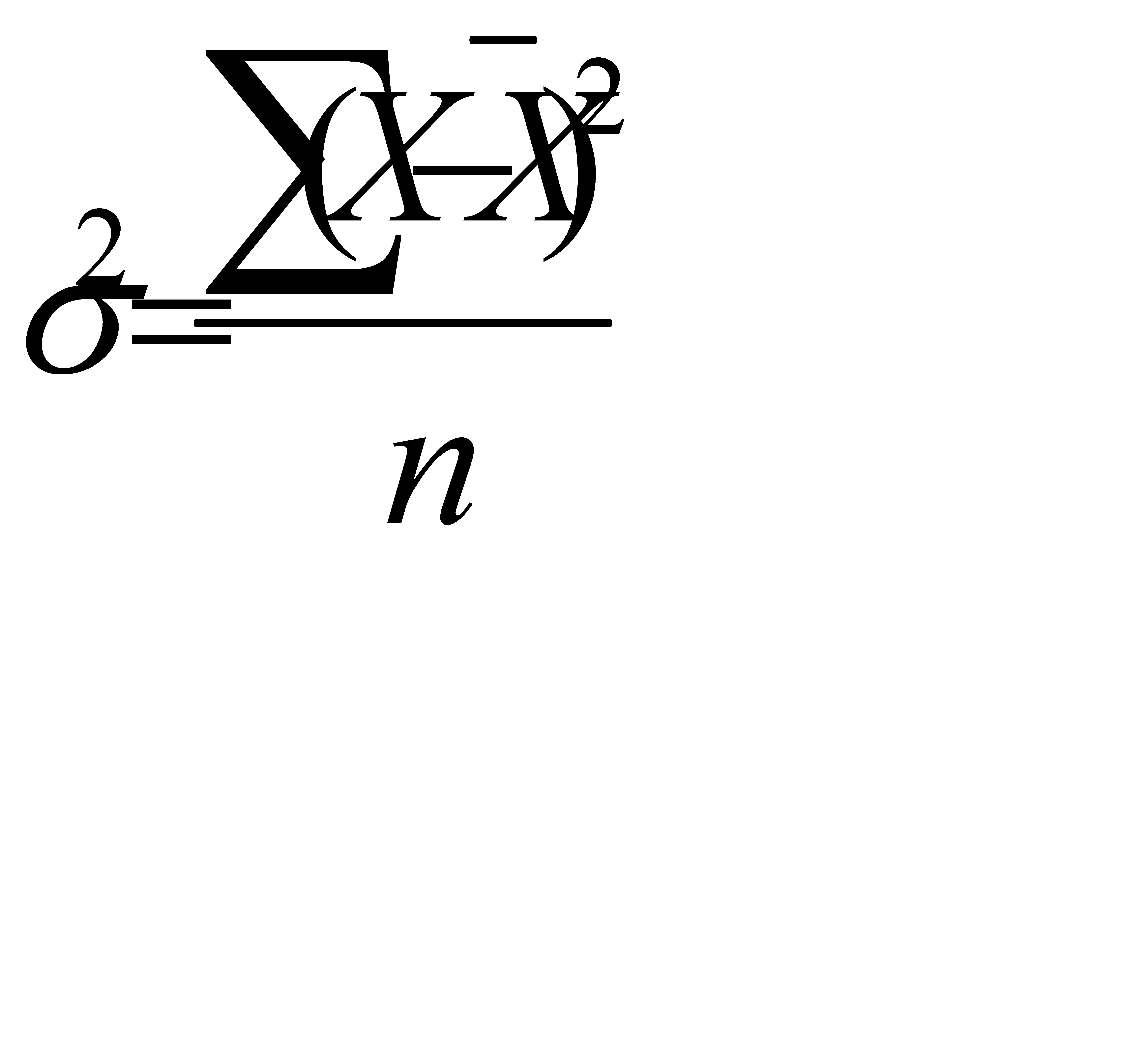(5.6)

для сгруппированных данных:

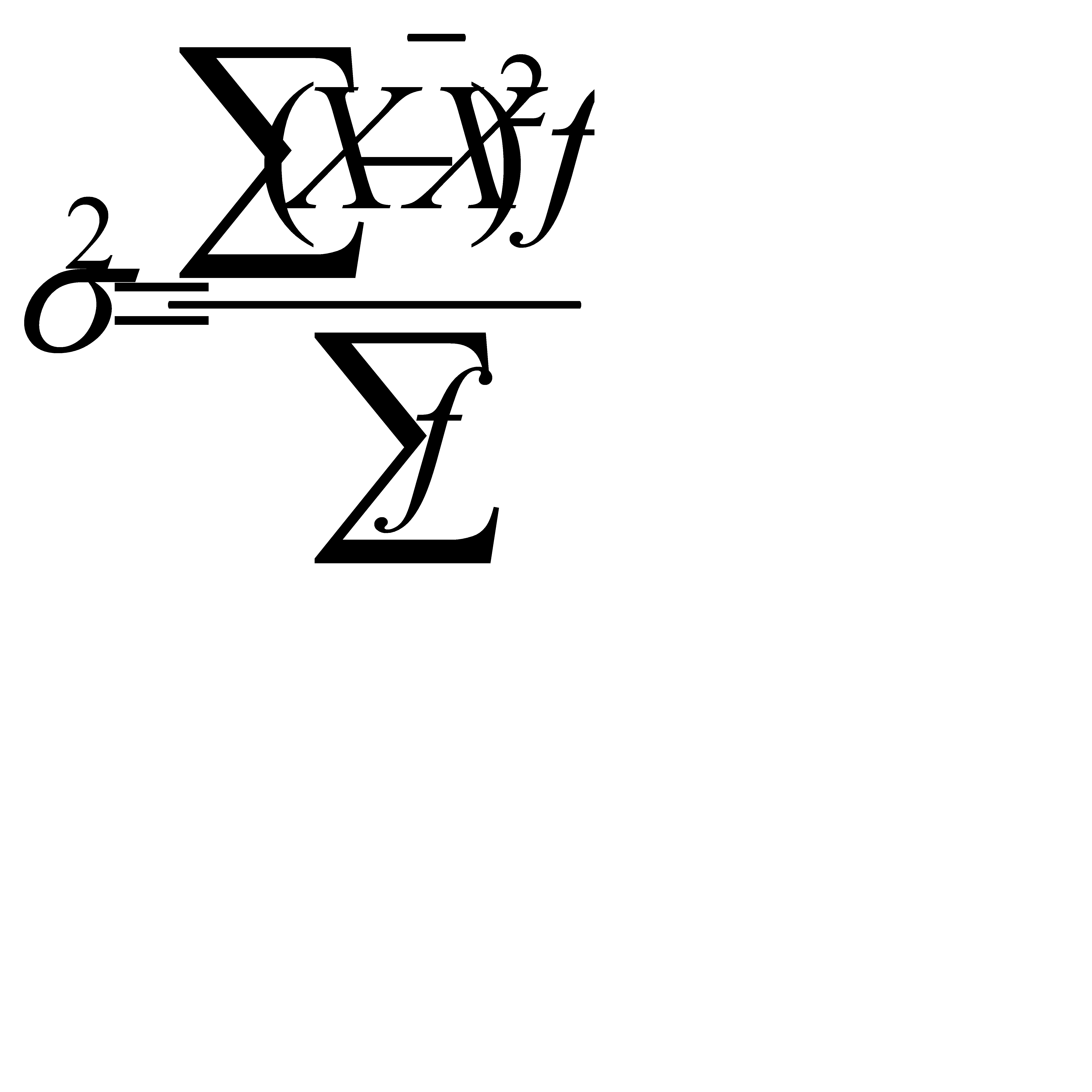. (5.7)

Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:

(5.8)

Чем меньше значение линейного и среднеквадратического отклонения, тем меньше вариация признака в совокупности.

Рассмотренные абсолютные характеристики вариации – именованные величины, имеют единицы измерения варьирующего признака.