Методы определения и свойства дисперсии

Дисперсия обладает рядом свойств (доказываемых в математической статистике), которые позволяют упростить расчеты.

1 способ. Дисперсия определяется как разность между средней квадратов вариантов и квадратом их средней:

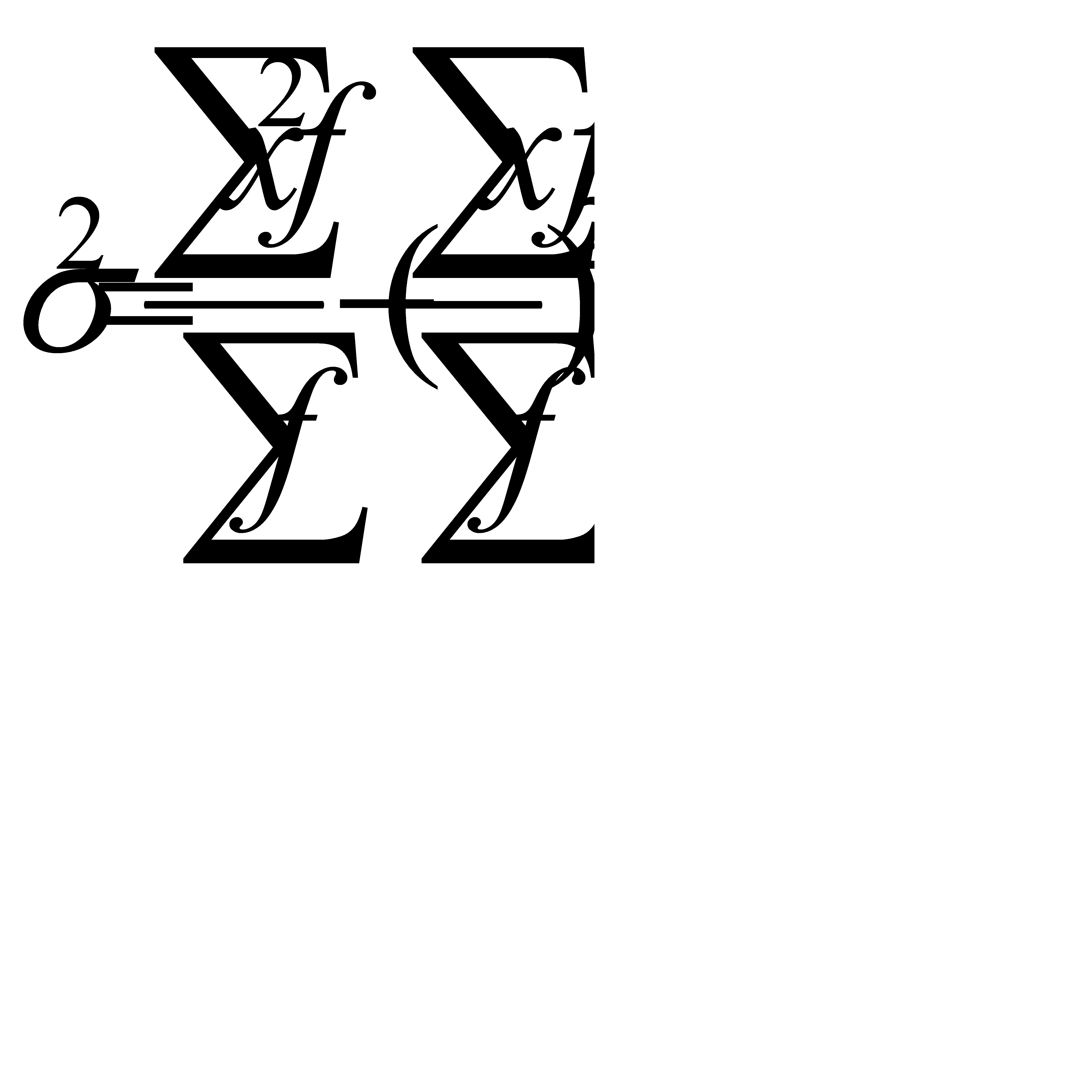. (5.13)

2 способ. Способ отсчета от условного нуля или способ моментов. Используется при условии равных интервалов.

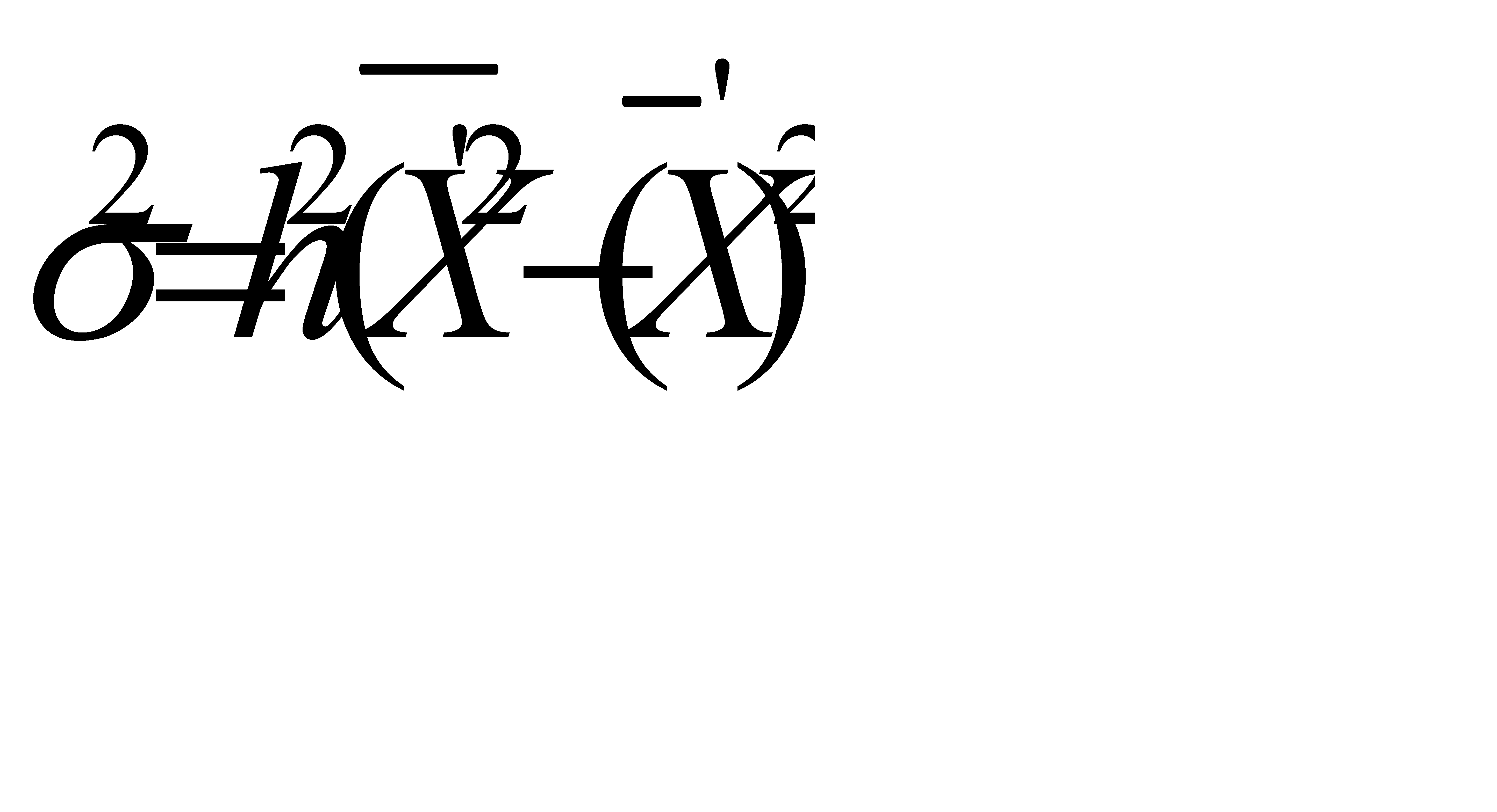. (5.14)

Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком (р), и доли единиц, не обладающих им(q) :

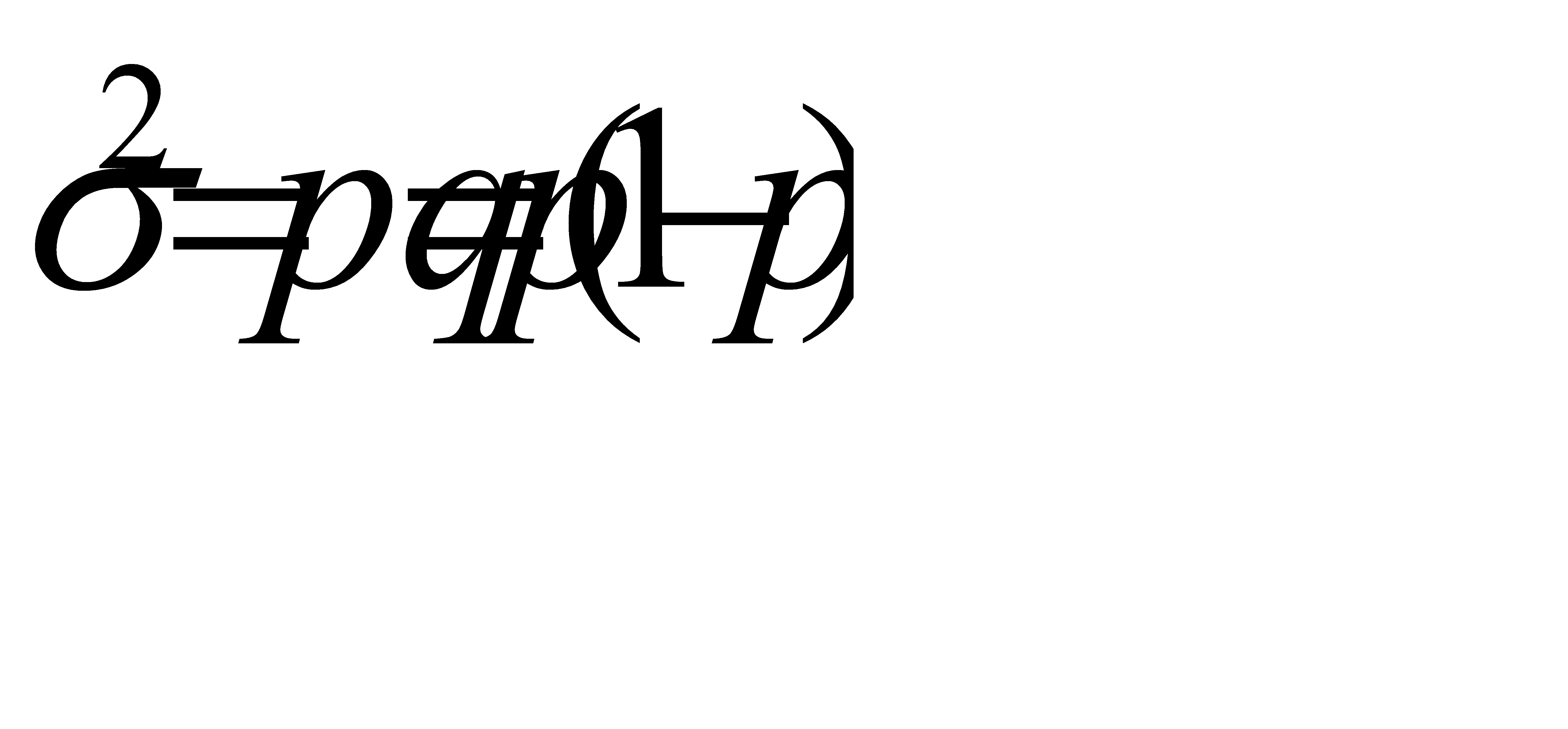. (5.15)

Изучая дисперсию признака в пределах изучаемой совокупности мы не можем определить влияние отдельных (случайных) факторов, характеризующих колеблемость индивидуальных значений признака. Это можно сделать при помощи группировок, разделив изучаемую совокупность на группы, однородные по признаку – фактору. При этом определяется три показателя вариации признака в совокупности: общая дисперсия, межгрупповая дисперсия и средняя из внутригрупповых дисперсий.

Общая дисперсия характеризует вариацию признака, которая зависит от всех факторов. Она определяется по формуле:

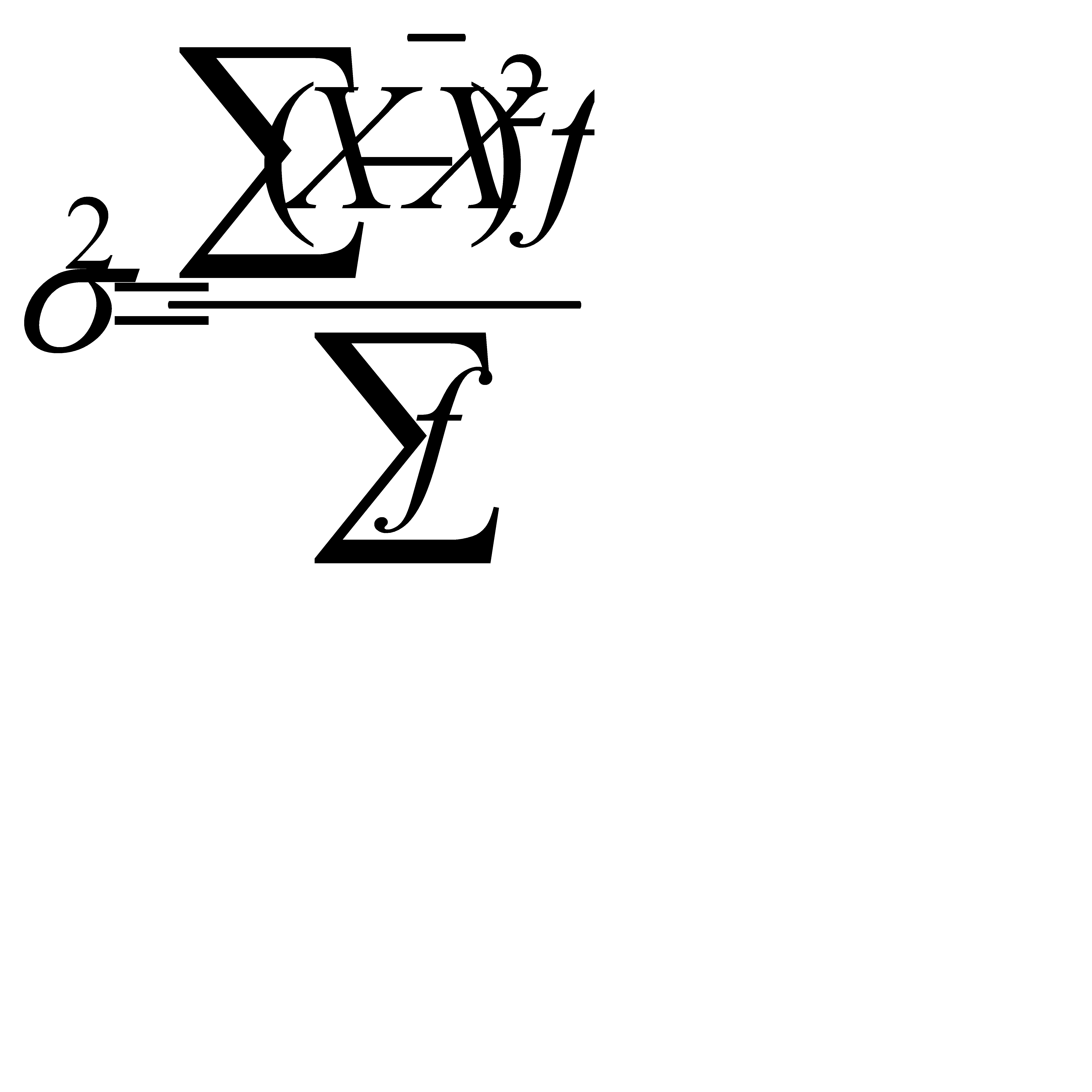. (5.16)

Межгрупповая дисперсия отражает вариацию изучаемого признака под влиянием признака – фактора, положенного в основу группировки. Она характеризует колеблемость групповых средних около общей средней:

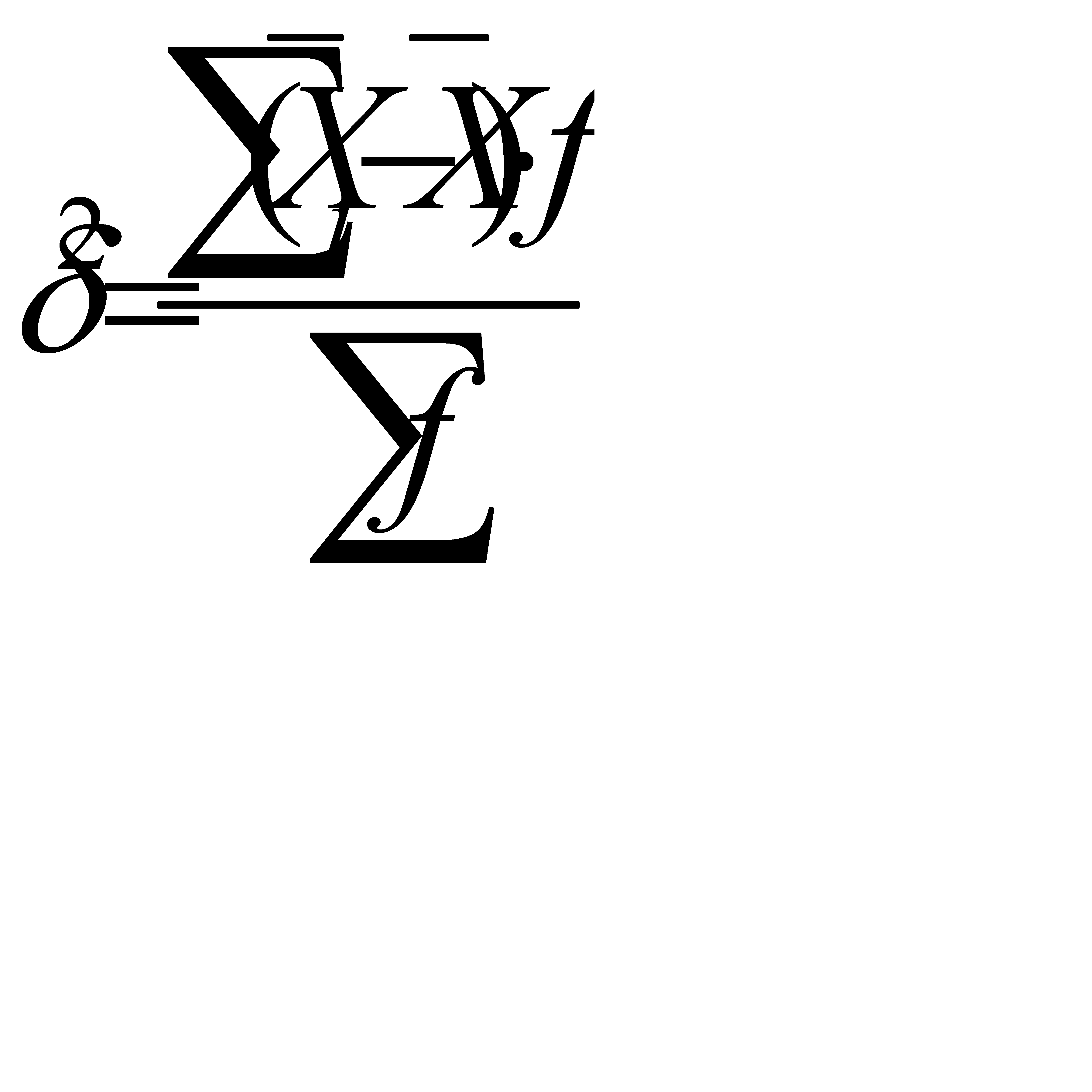. (5.17)

Средняя из внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием случайных, не учтенных факторов и не зависит от фактора, положенного в основу группировки:

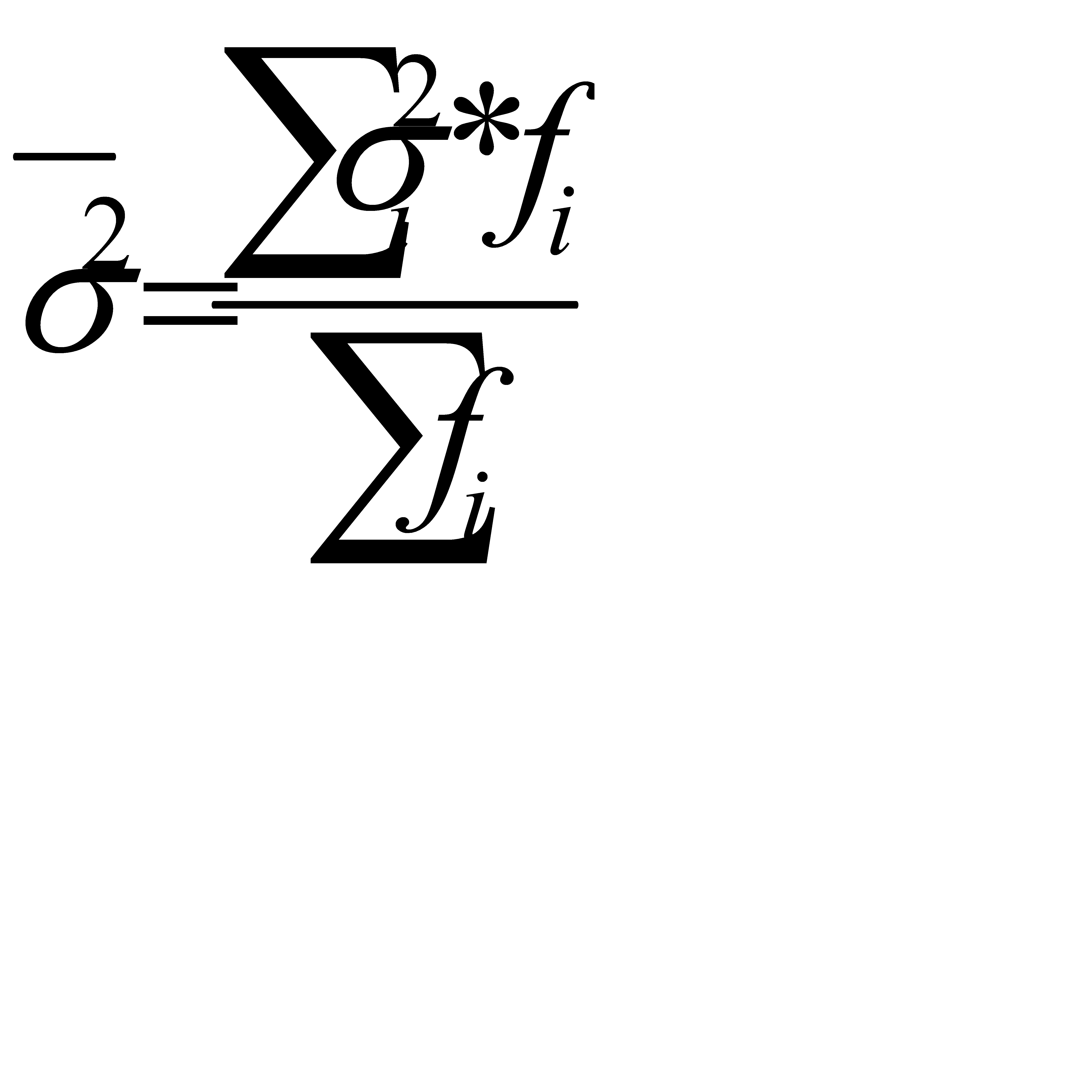. (5.18)

Между этими дисперсиями существует соотношение, определяемое правилом сложения дисперсий. Согласно этому правилу, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

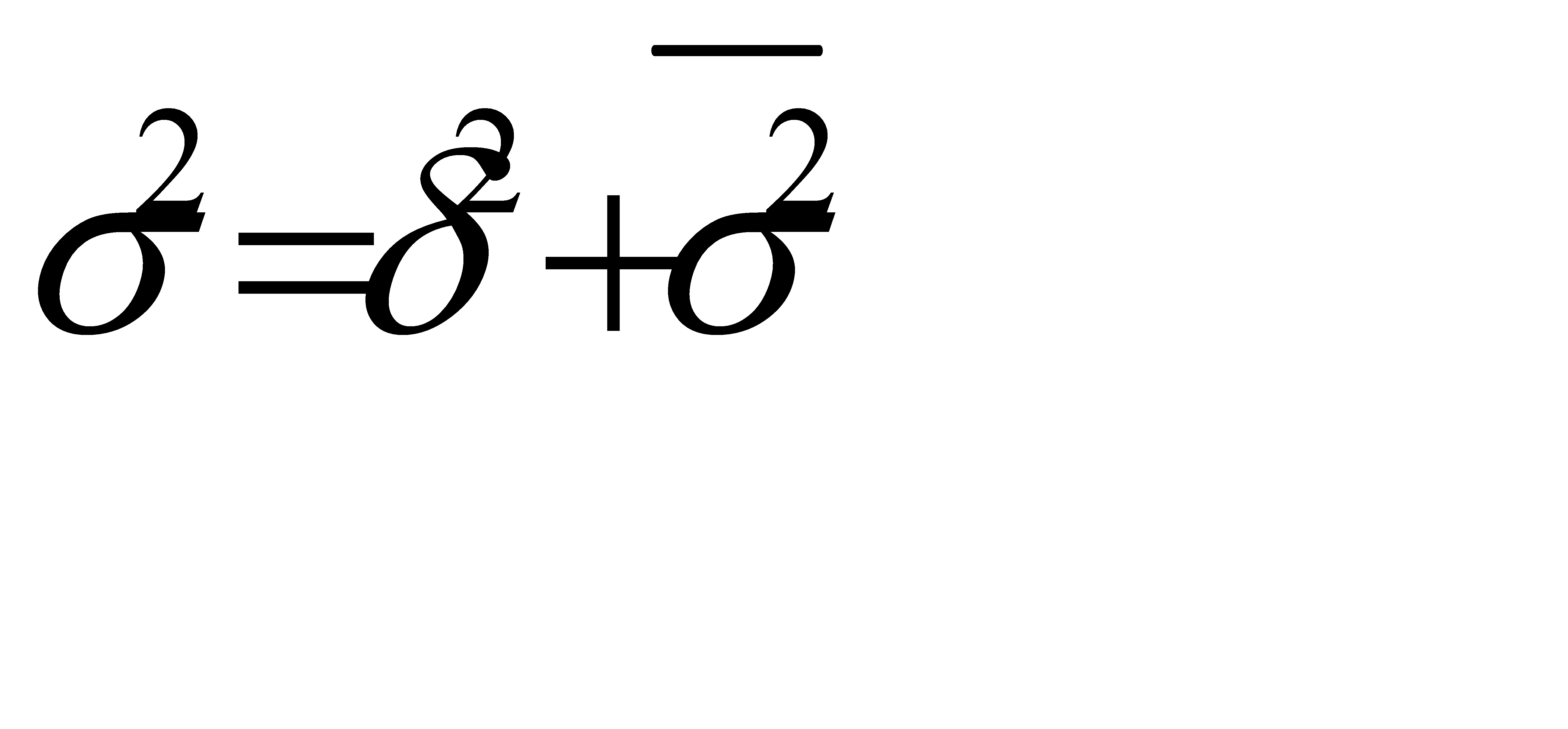. (5.19)

Это правило имеет большую практическую значимость, т.к. позволяет выявить зависимость результатов от определяющих факторов. Отношение межгрупповой дисперсии к общей позволяет судить о связи между изучаемыми признаками и называется коэффициентом детерминации ( ):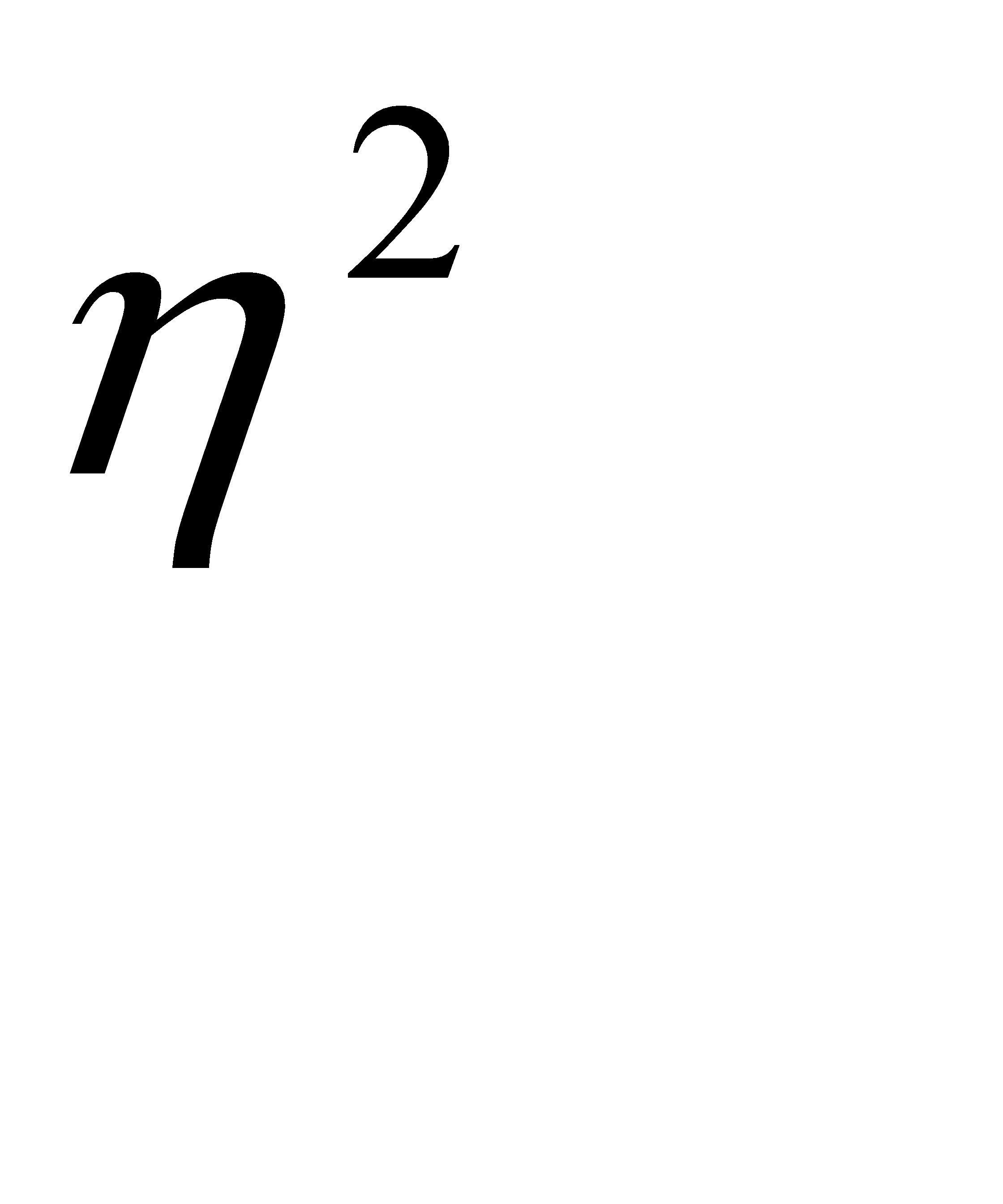

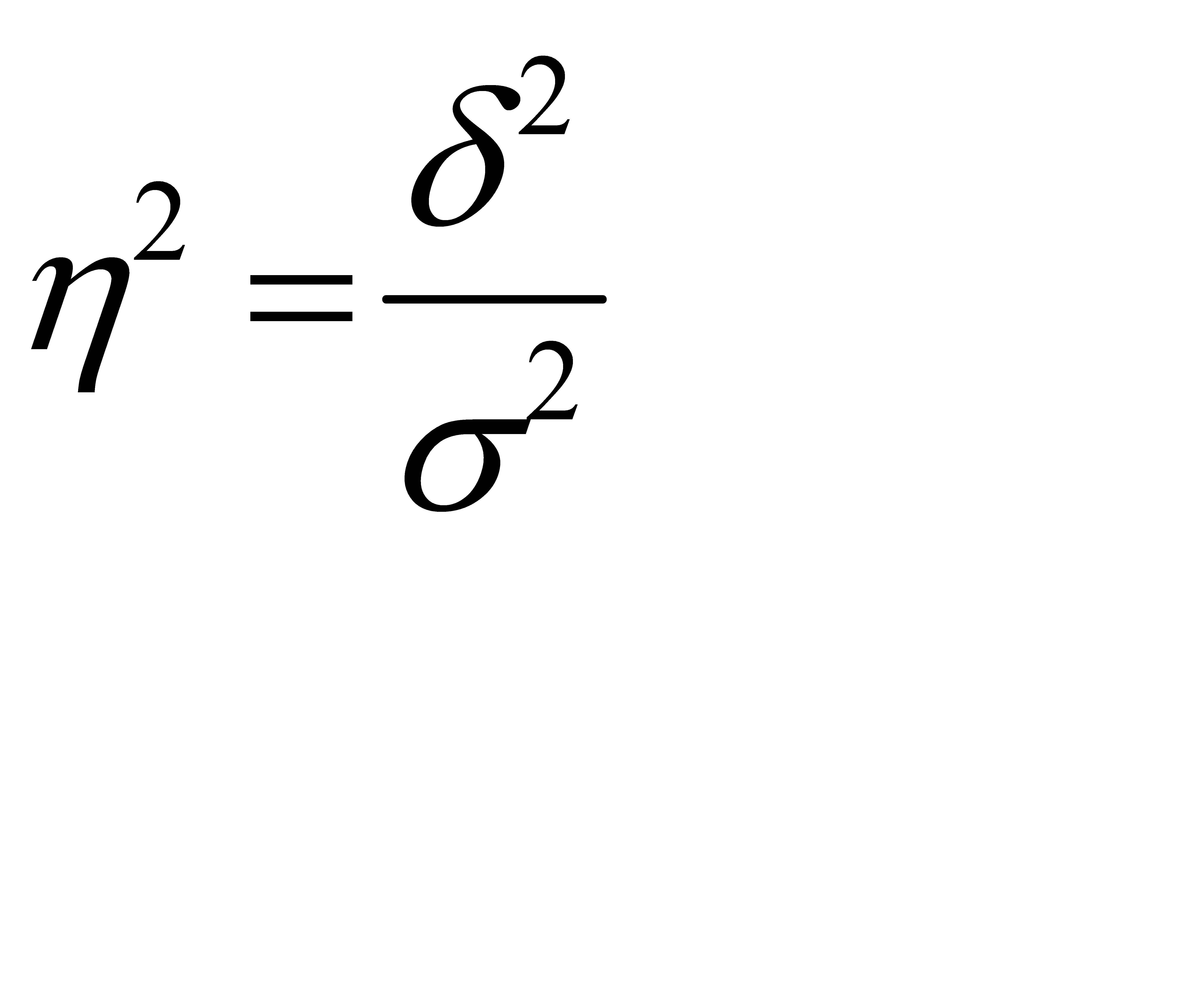. (5.20)