Характеристика закономерности рядов распределения
Выяснение общего характера эмпирического распределения предполагает оценку его однородности, а также вычисление показателей асимметрии и эксцесса.
Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих от центра распределения, равны между собой. Для симметричных распределений:
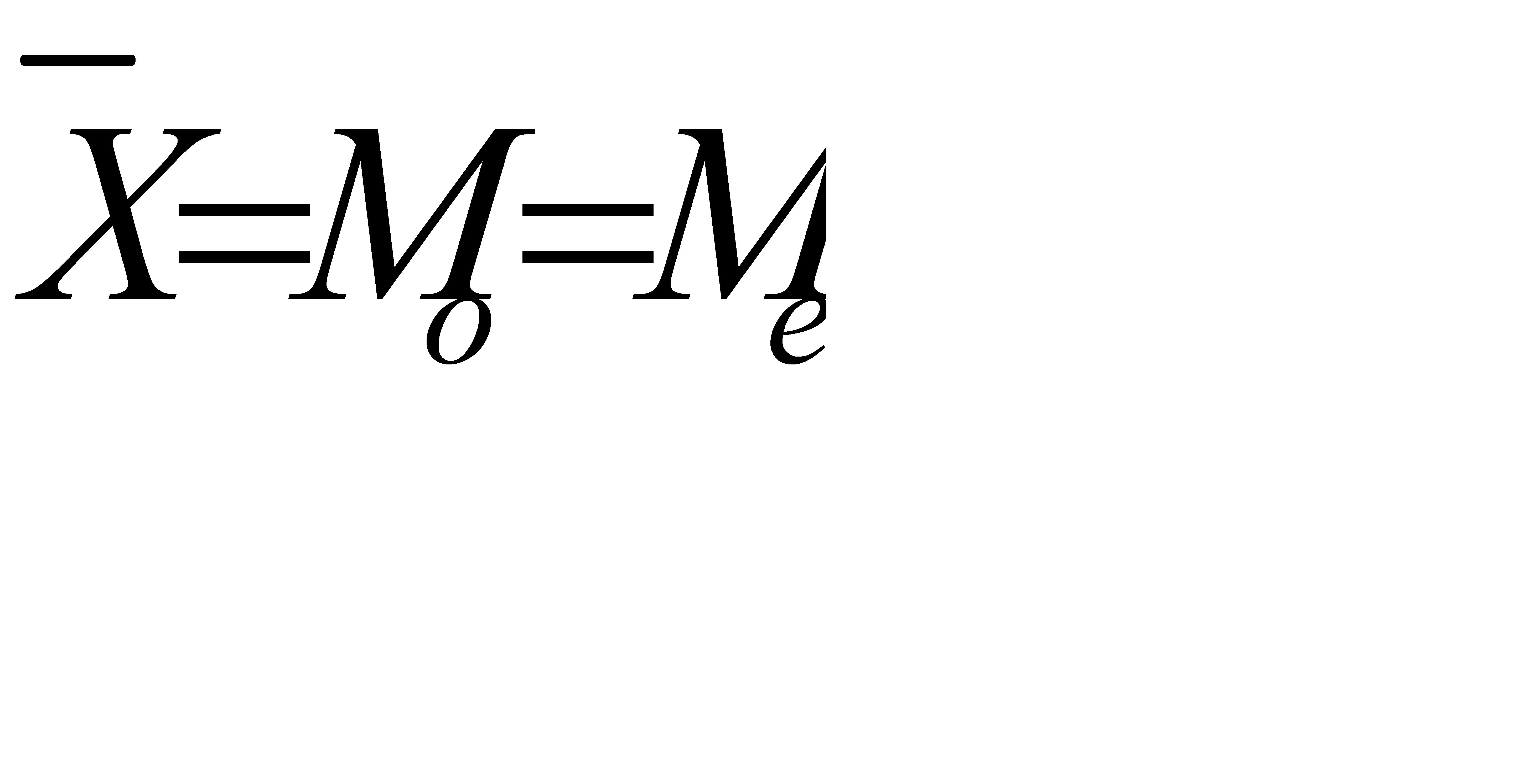. (5.21)
Величина показателя асимметрии может быть положительной и отрицательной. Положительное значение свидетельствует о наличии правосторонней асимметрии, отрицательное – о наличии левосторонней асимметрии.
Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка:
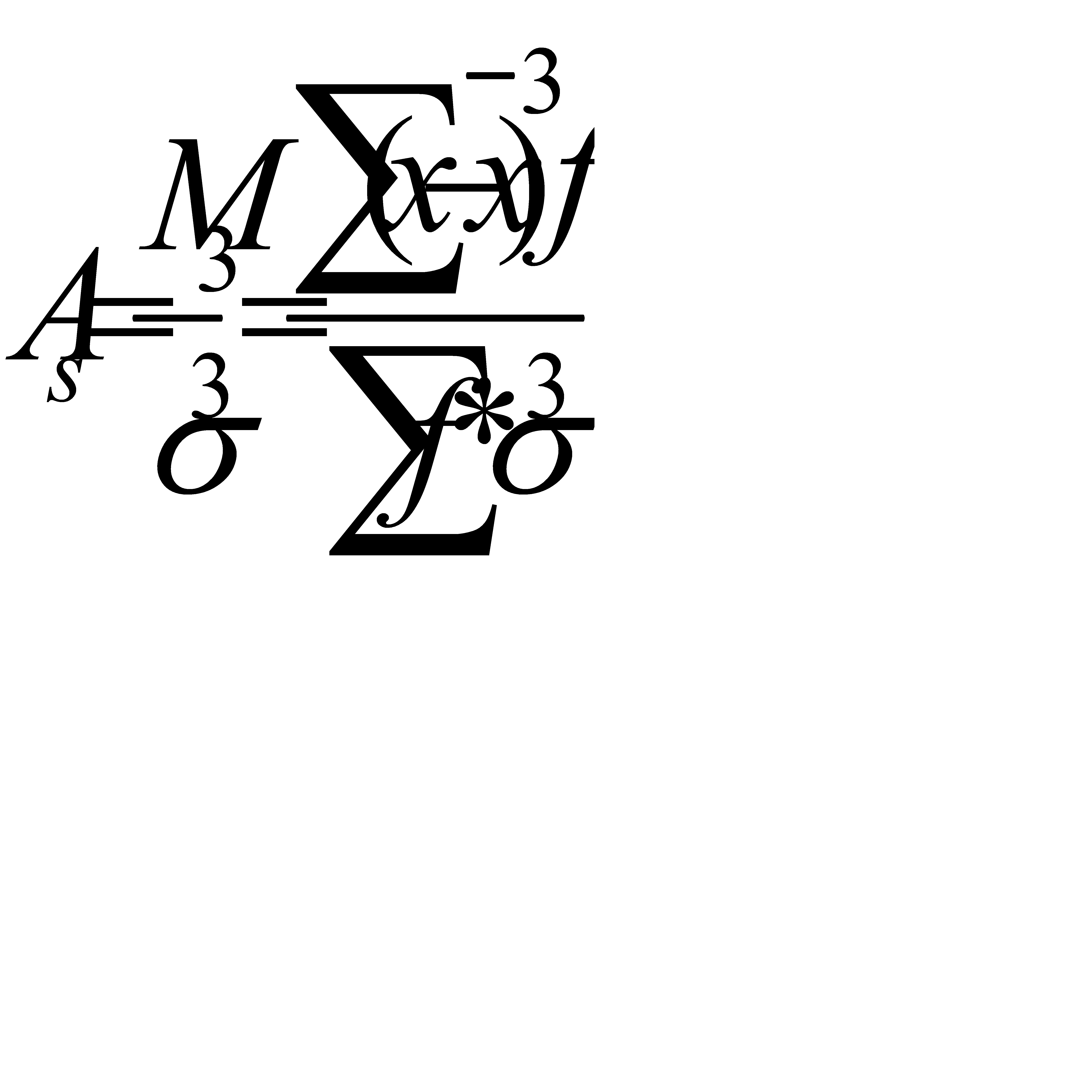, (5.22)
Если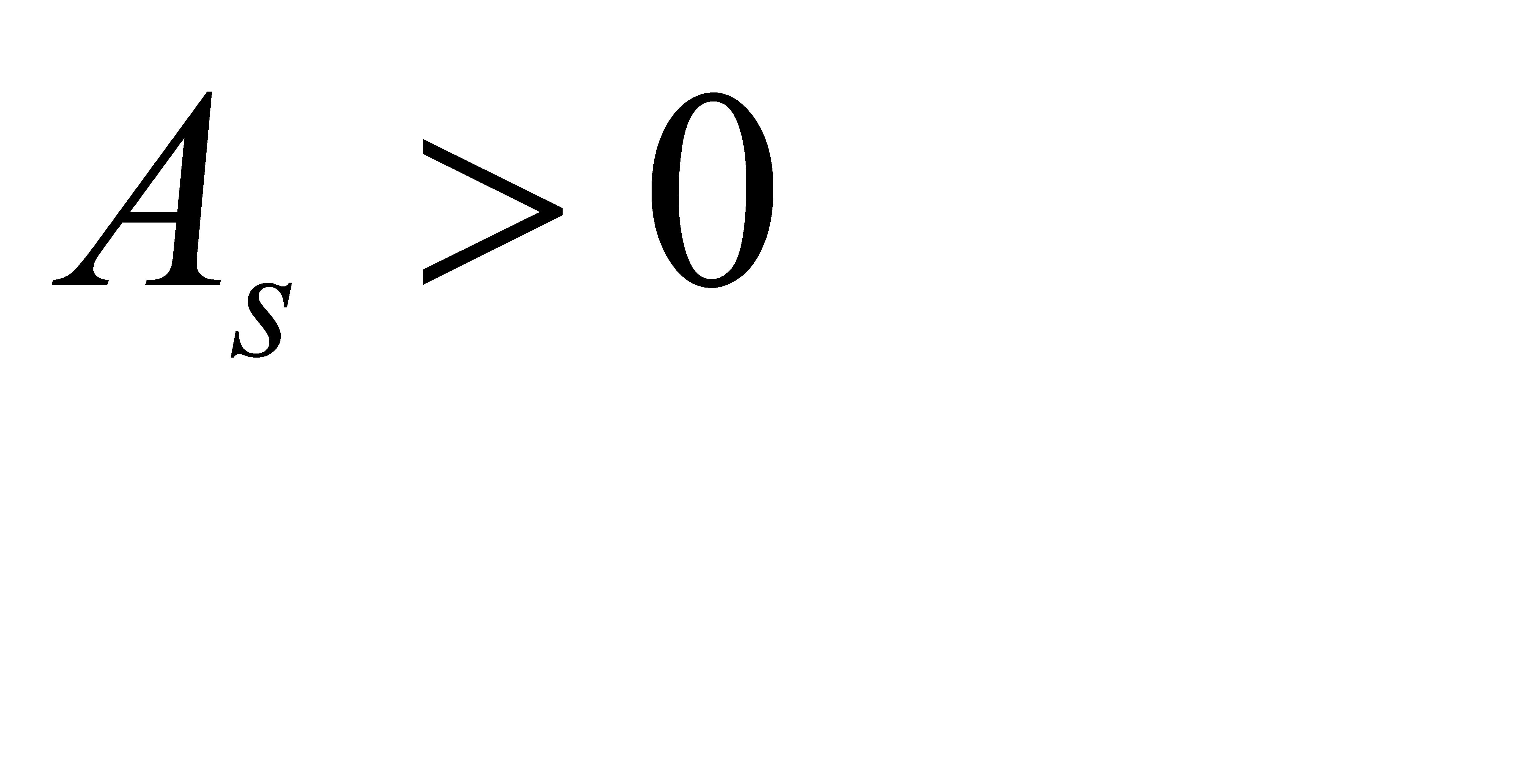 
, асимметрия правосторонняя со смещением влево.
Оценка степени точности этого показателя определяется с помощью средней квадратической ошибки, которая зависит от объема наблюдений.
Эксцесс характеризует отклонение вершины эмпирического распределения вверх или вниз от вершины нормального распределения.
Наиболее точным является показатель, основанный на определении момента четвертого порядка:
, (5.23)
Если Eх<3 - распределение плосковершинное.
Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли данное распределение отнести к нормальному.
Контрольные вопросы
1. Что такое вариация признаков?
2. Как следует понимать закономерность распределения? Можно ли ее количественно измерить?
3. По какой формуле целесообразно рассчитывать дисперсию, если средняя – дробное число, например, 1,5?
4. Можно ли сравнить вариация двух признаков, имеющих разное выражение?
5. Изменится ли дисперсия, если все значения признака разделить (умножить) на одну и ту же величину?
6. Как определяется дисперсия альтернативного признака?
7. Какие Вы знаете показатели измерения вариации признаков?
8. Что показывает коэффициент вариации, и для какой цели его рассчитывают?
9. Чем характеризуется ряд распределения?
10. Что представляет собой кумулятивный ряд?
11. Что показывают коэффициенты асимметрии и эксцесса?
Дата добавления: 2016-03-15; просмотров: 1093;