Расчет средней и предельной ошибки выборки. Определение границ интервала для средней и доли в генеральной совокупности

В математической статистике доказано, что для собственно – случайного и механического бесповторного отбора средняя ошибка выборки ( 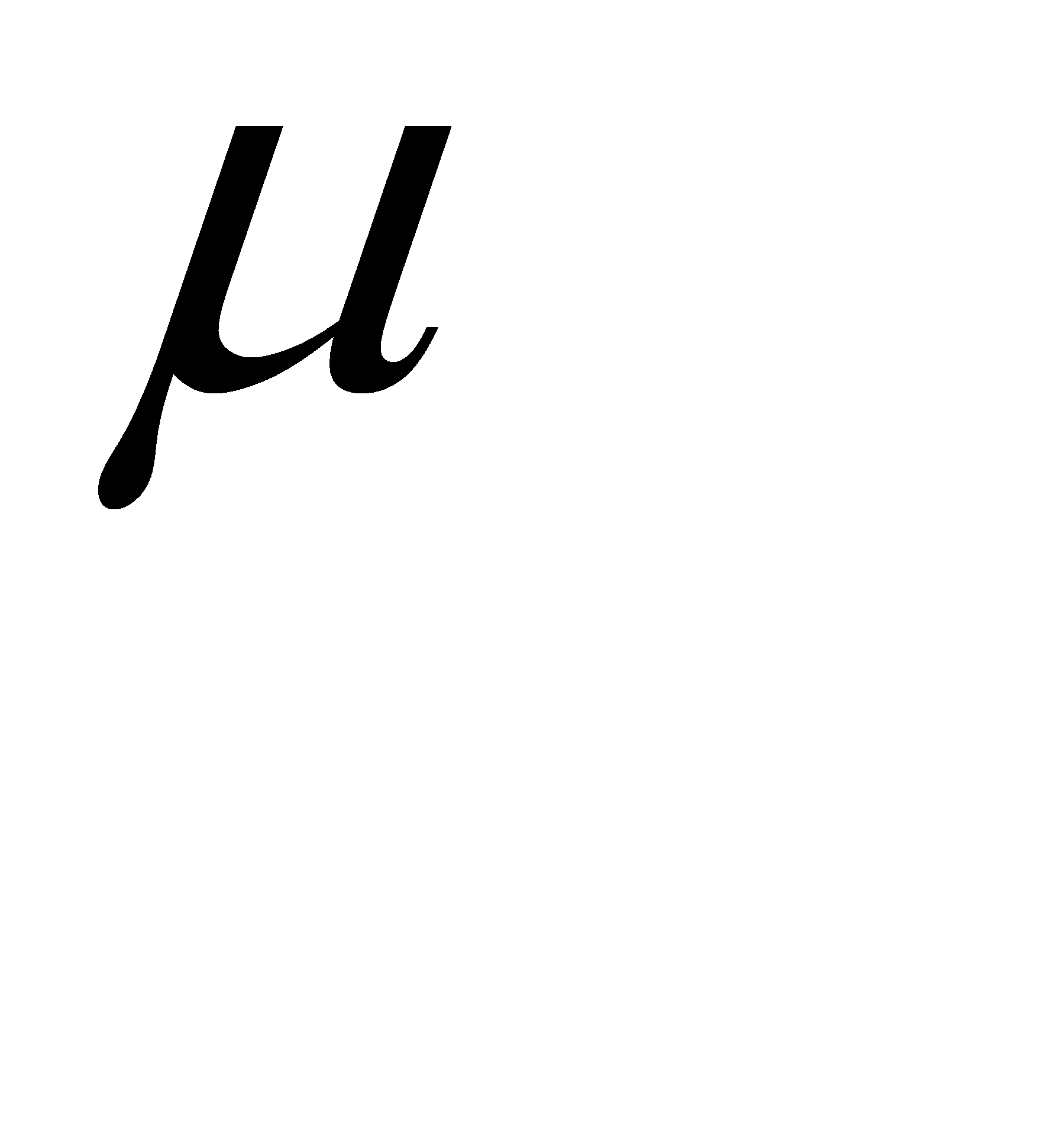) равна:

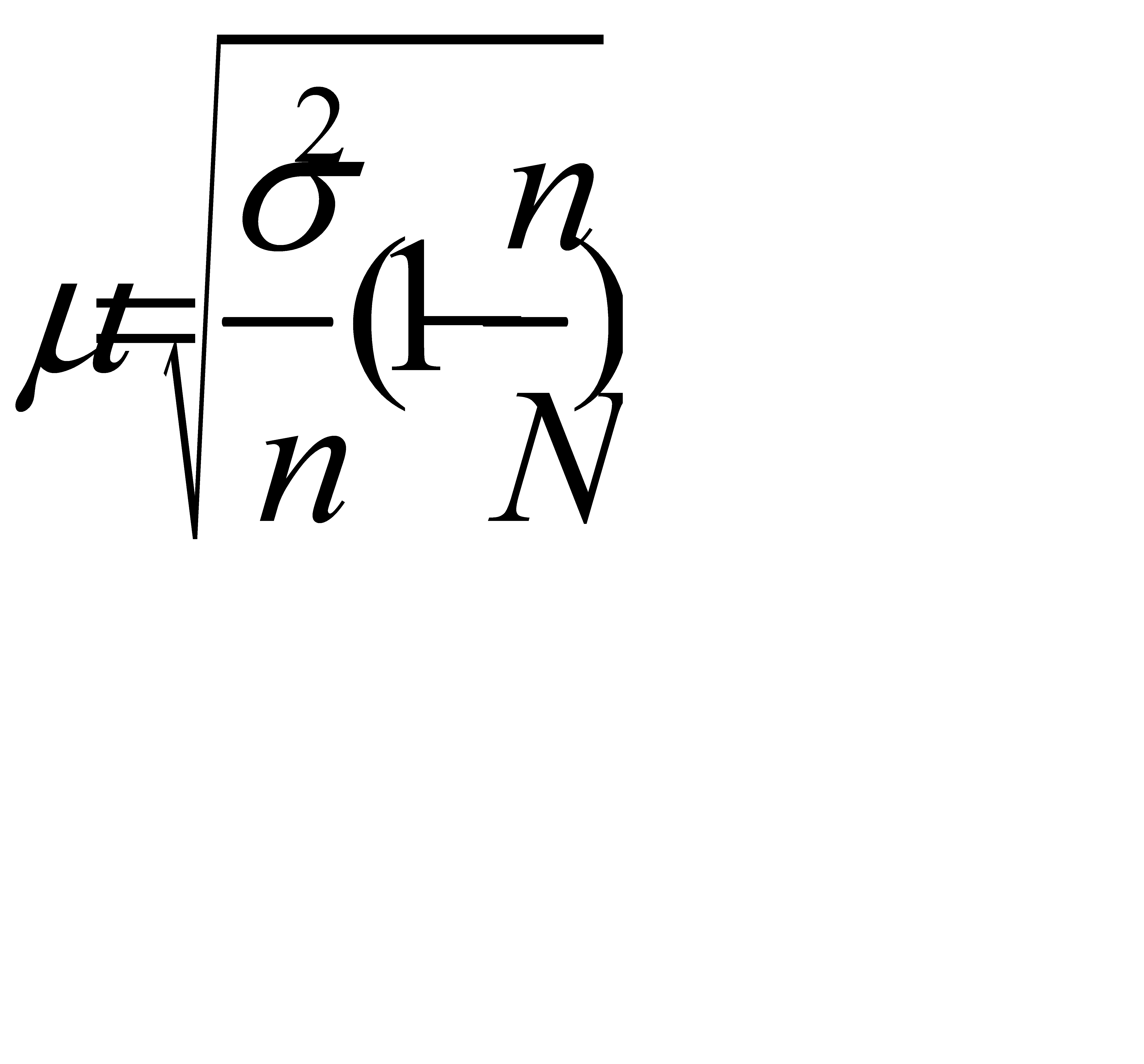, (6.1)

где N – объем генеральной совокупности;

n -объем выборочной совокупности;

σ² – общая дисперсия признака.

Средняя ошибка доли:

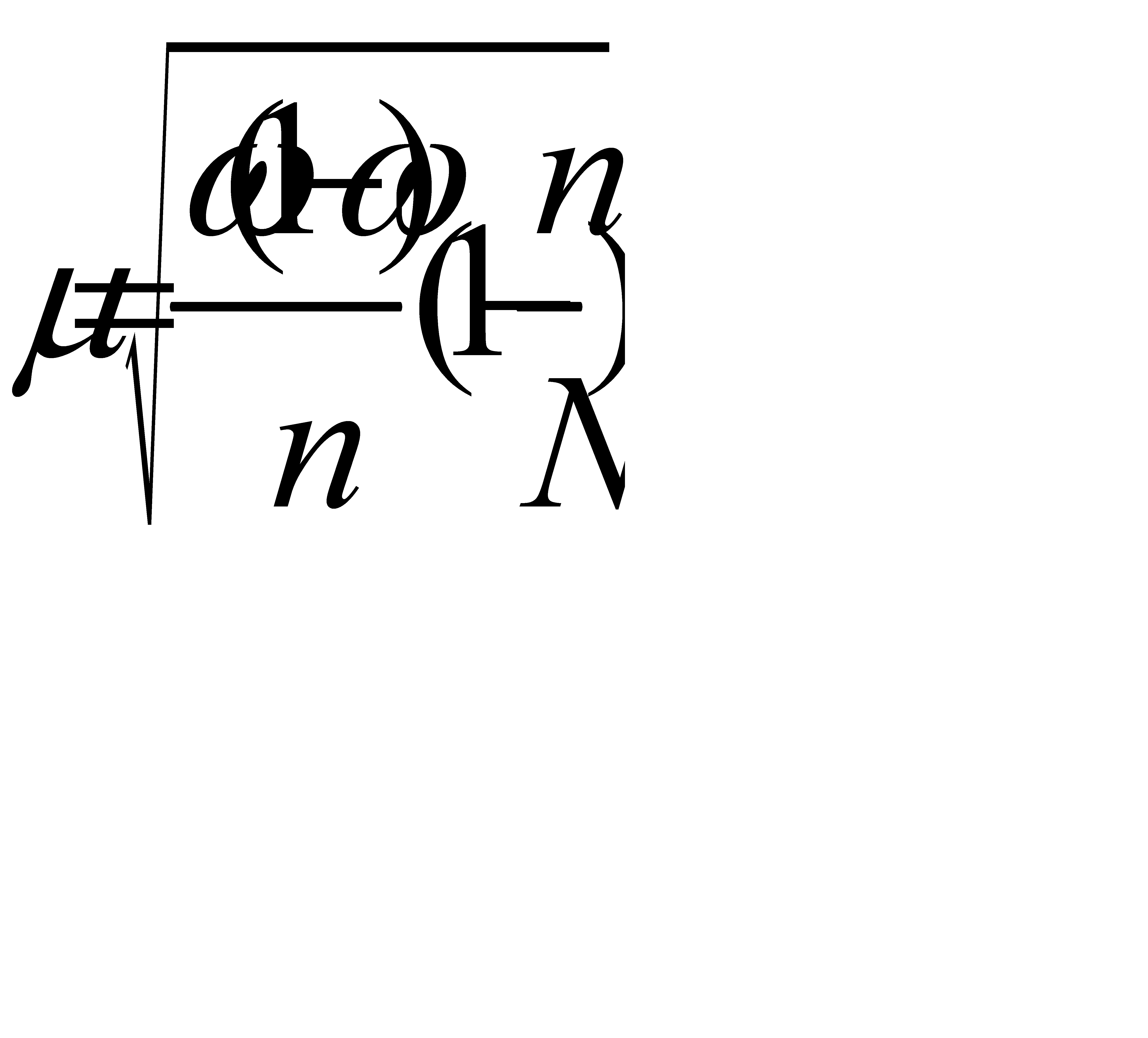, (6.2)

гдеω – доля альтернативного признака.

При собственно случайном и механическом повторном индивидуальном отборе средняя ошибка выборки:

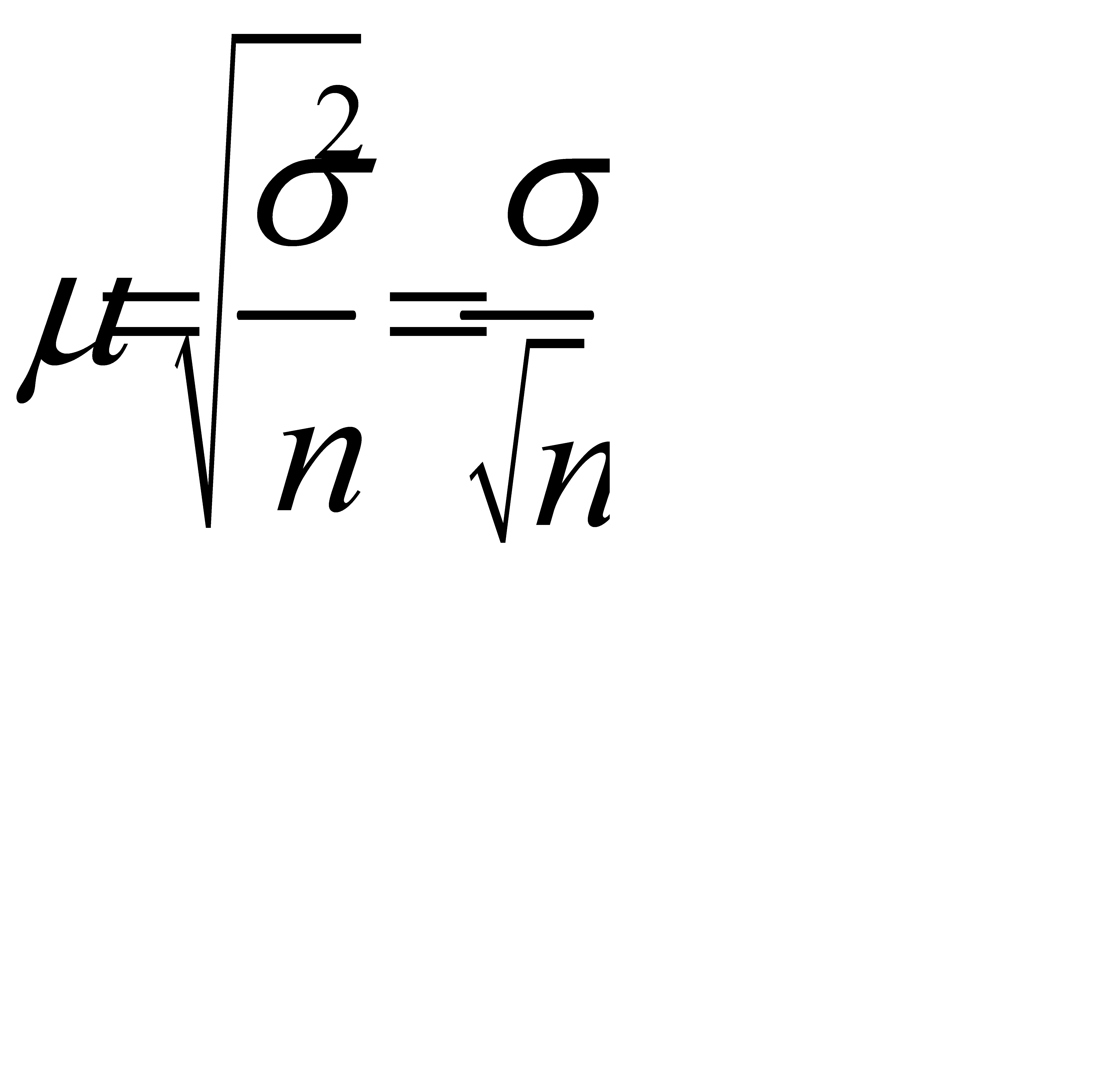(6.3)

Ошибка доли:

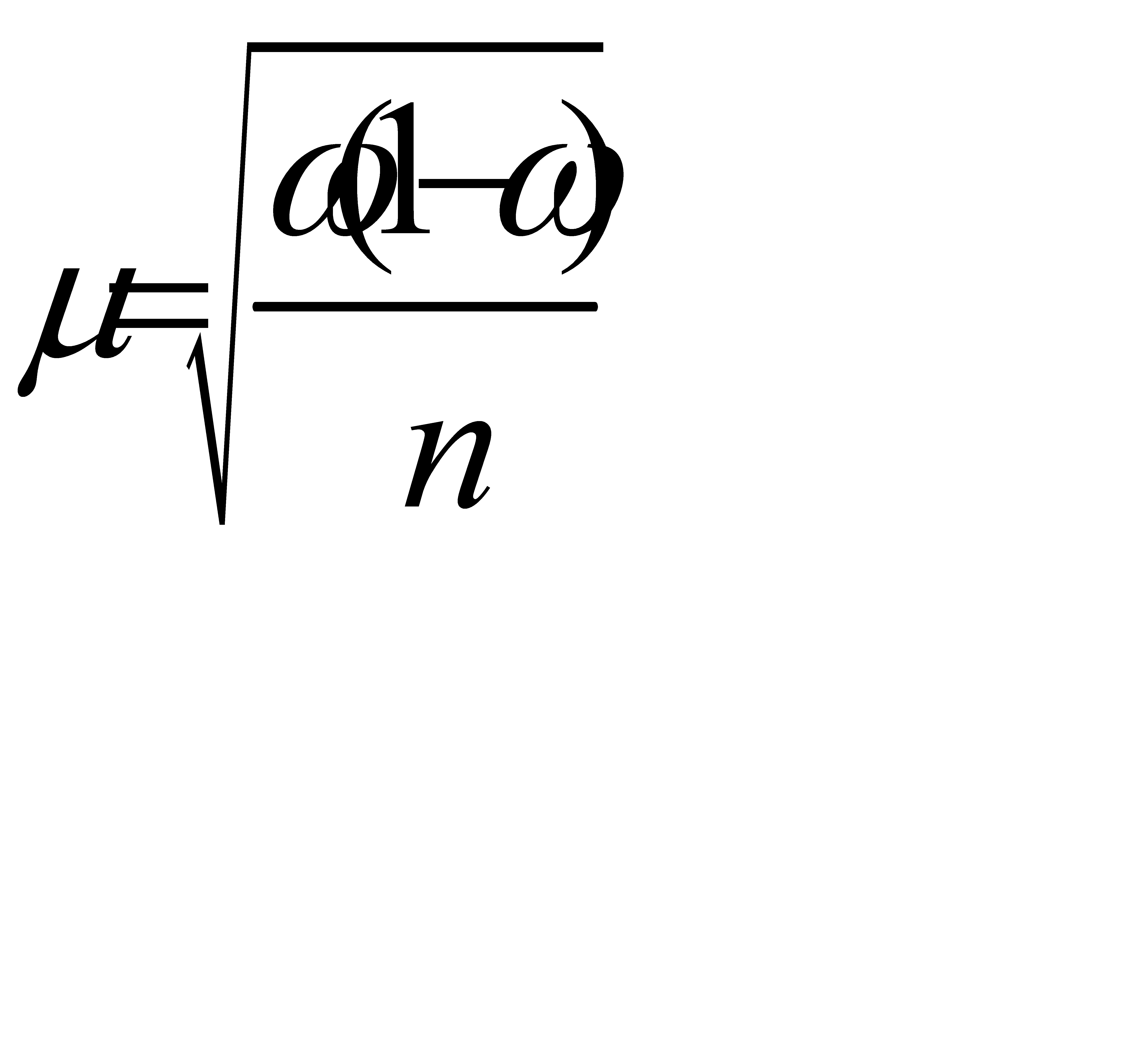. (6.4)

Для типического пропорционального бесповторного отбора:

При типическом бесповторном отборе:

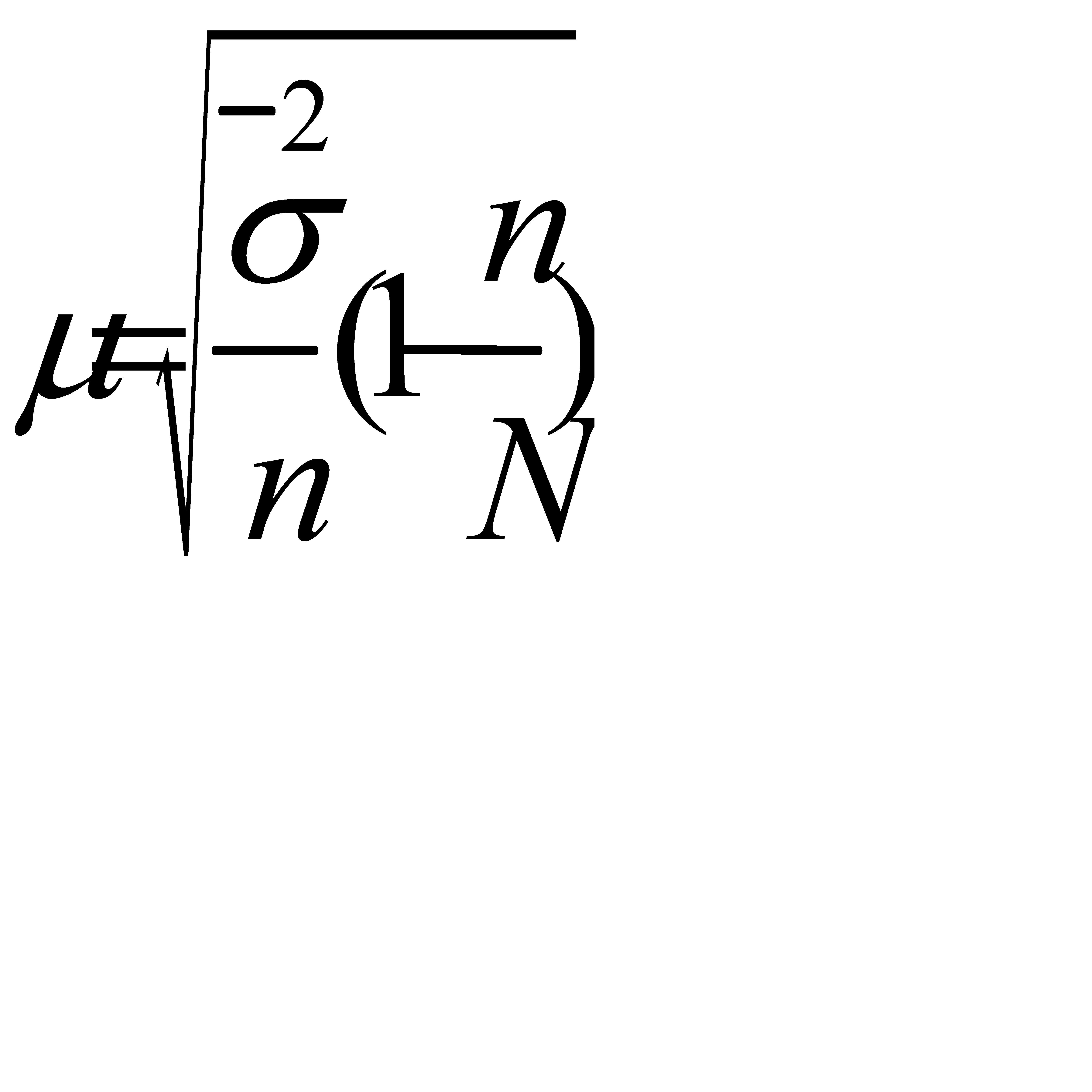, (6.5)

Где 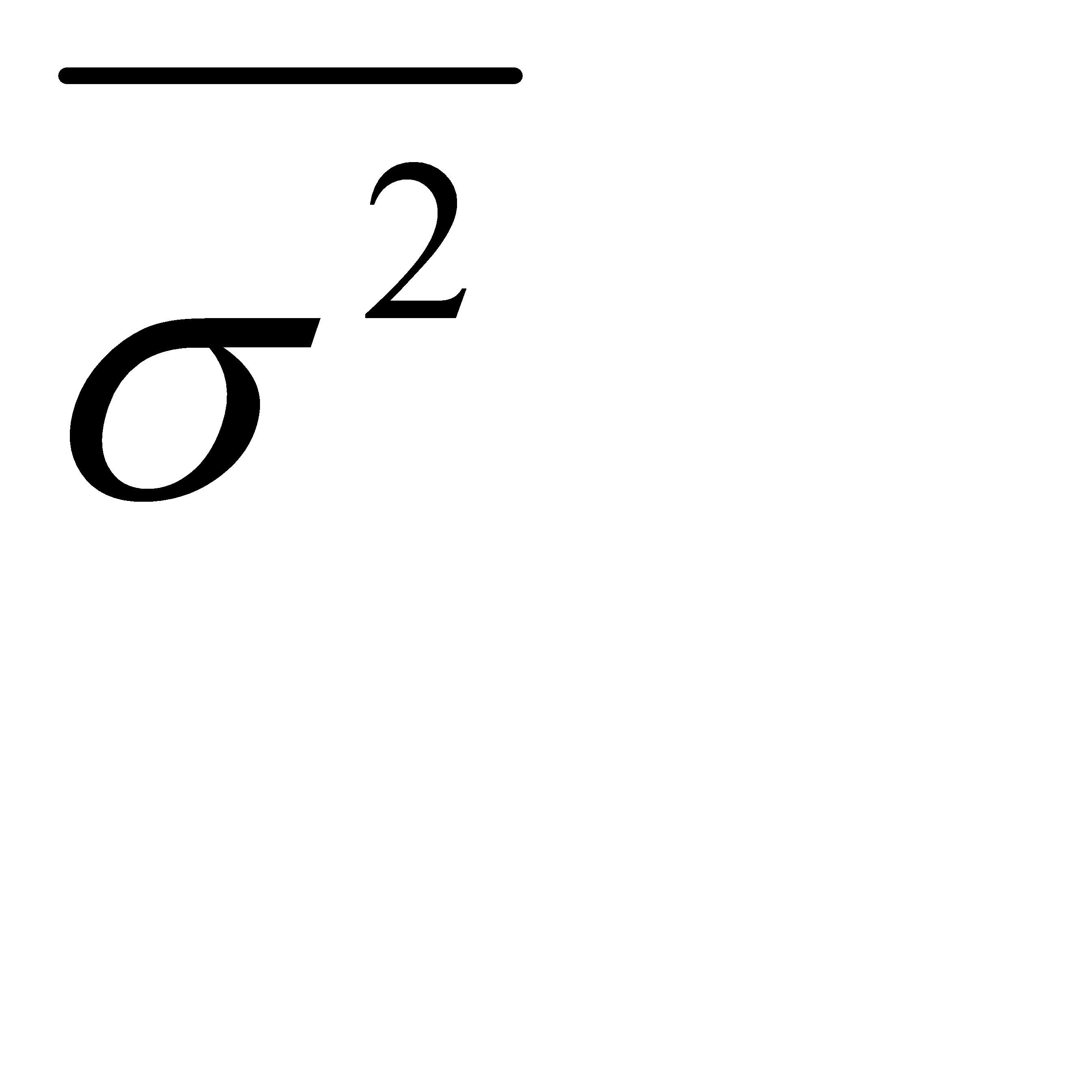– средняя из внутригрупповых дисперсий.

При типическом повторном отборе:

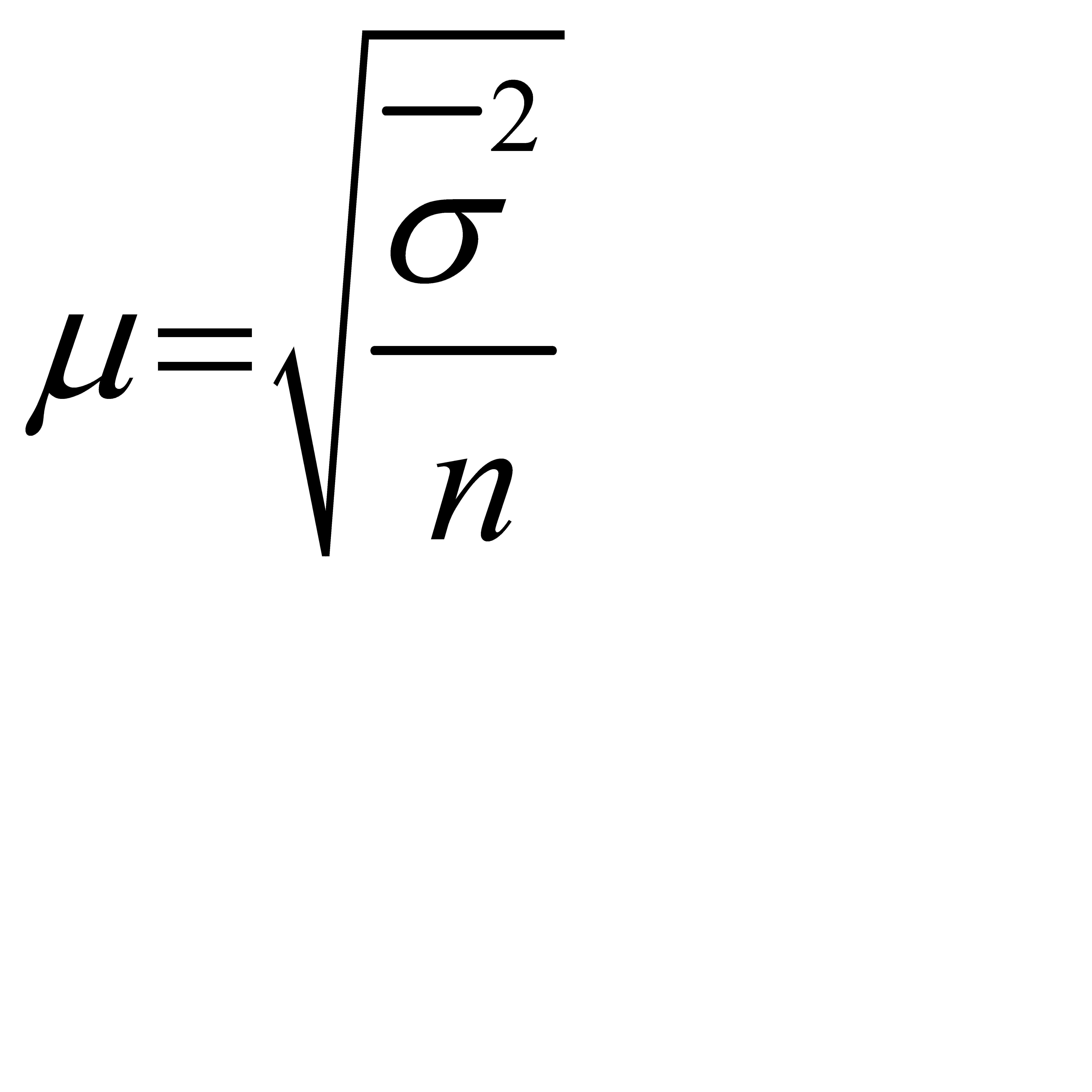. (6.6)

При бесповторном, серийном отборе:

, (6.7)

где r – число серий в выборке;

R – число серий в генеральной совокупности;

– межсерийная дисперсия выборочной средней.

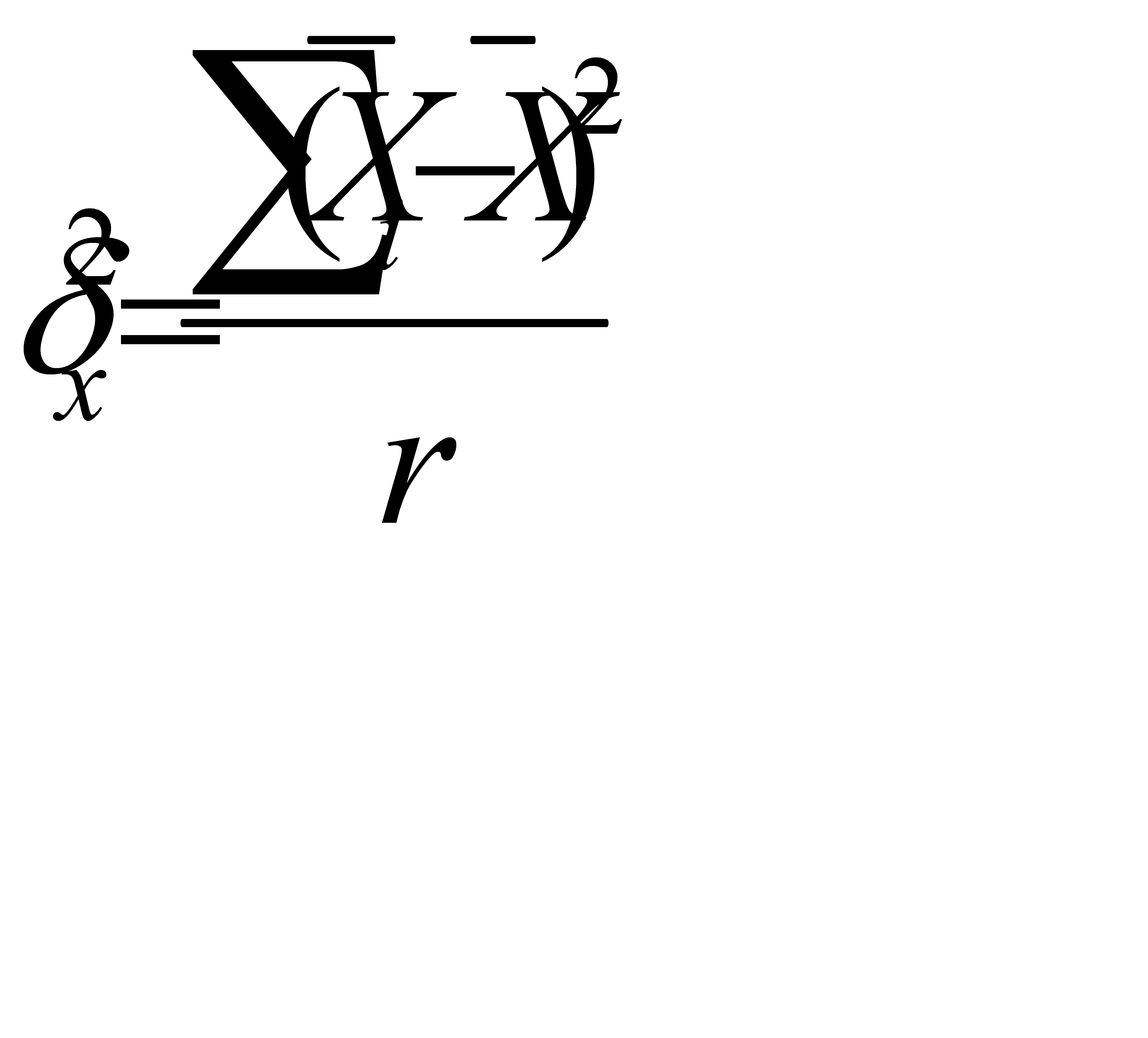. (6.8)

Средняя ошибка доли:

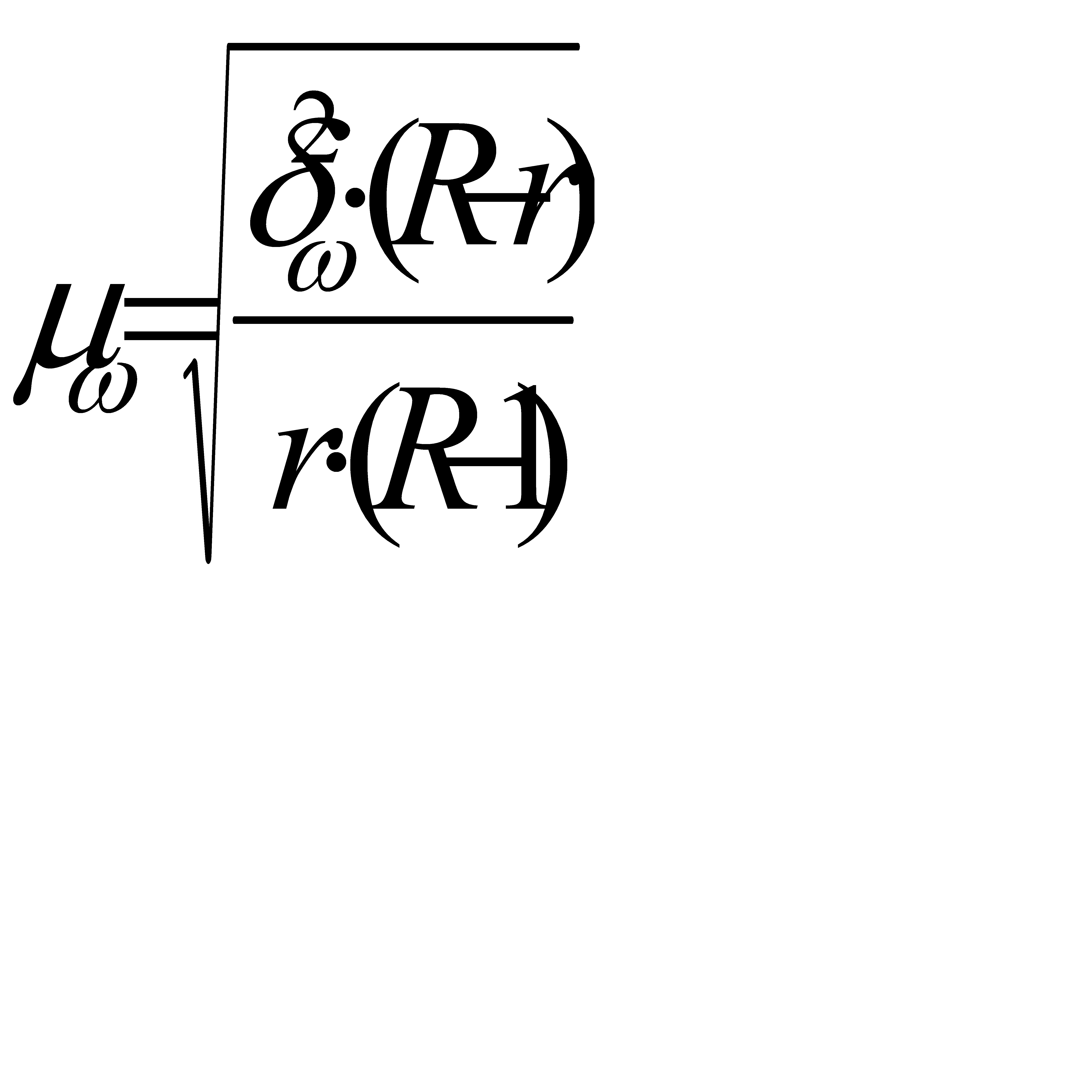, (6.9)

где – межсерийная дисперсия выборочной доли.

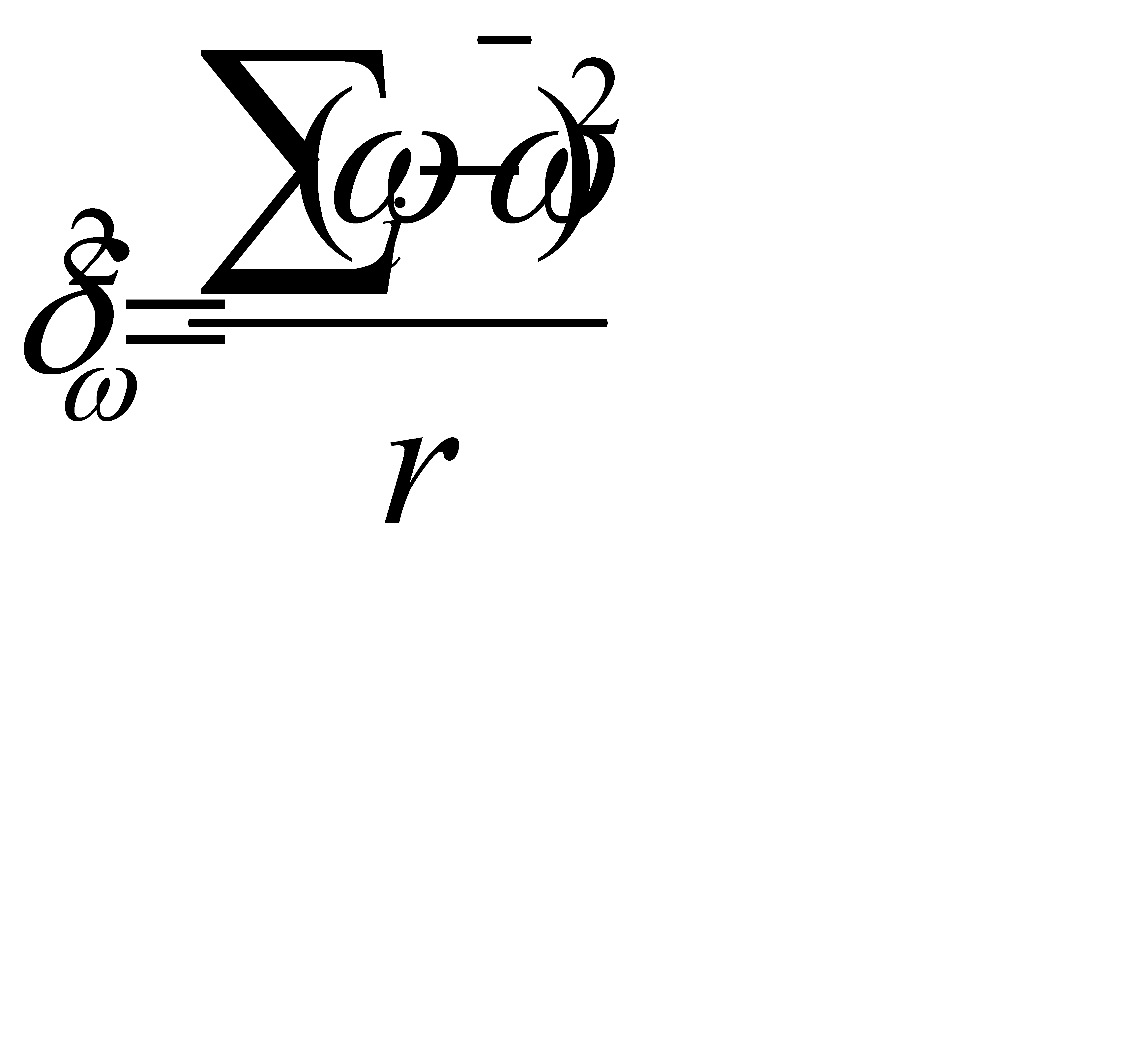. (6.10)

Средняя ошибка выборки характеризует меру отклонения выборочной средней (или доли) от генеральной средней (или доли).

В математической статистике доказывается, что с определенной вероятностью можно утверждать, что эти отклонения не превышают некоторую величину – предельную ошибку выборки. Распространение выборочных данных на генеральную совокупность производится с учетом доверительных интервалов.

Для решения практических задач пользуются предельной ошибкой выборки. Предельная ошибка выборки (Δ) определяется на основании средней ошибки выборки:

, (6.11)

где t –коэффициент доверия, зависящий от того, с какой вероятностью надо гарантировать результаты выборочного обследования. Доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента.

В экономических исследованиях обычно ограничиваются следующими значениями:

- для вероятности 0,683 t = 1;

- для вероятности 0,954 t = 2;

- для вероятности 0,997 t = 3.

Возможные границы средней в генеральной совокупности:

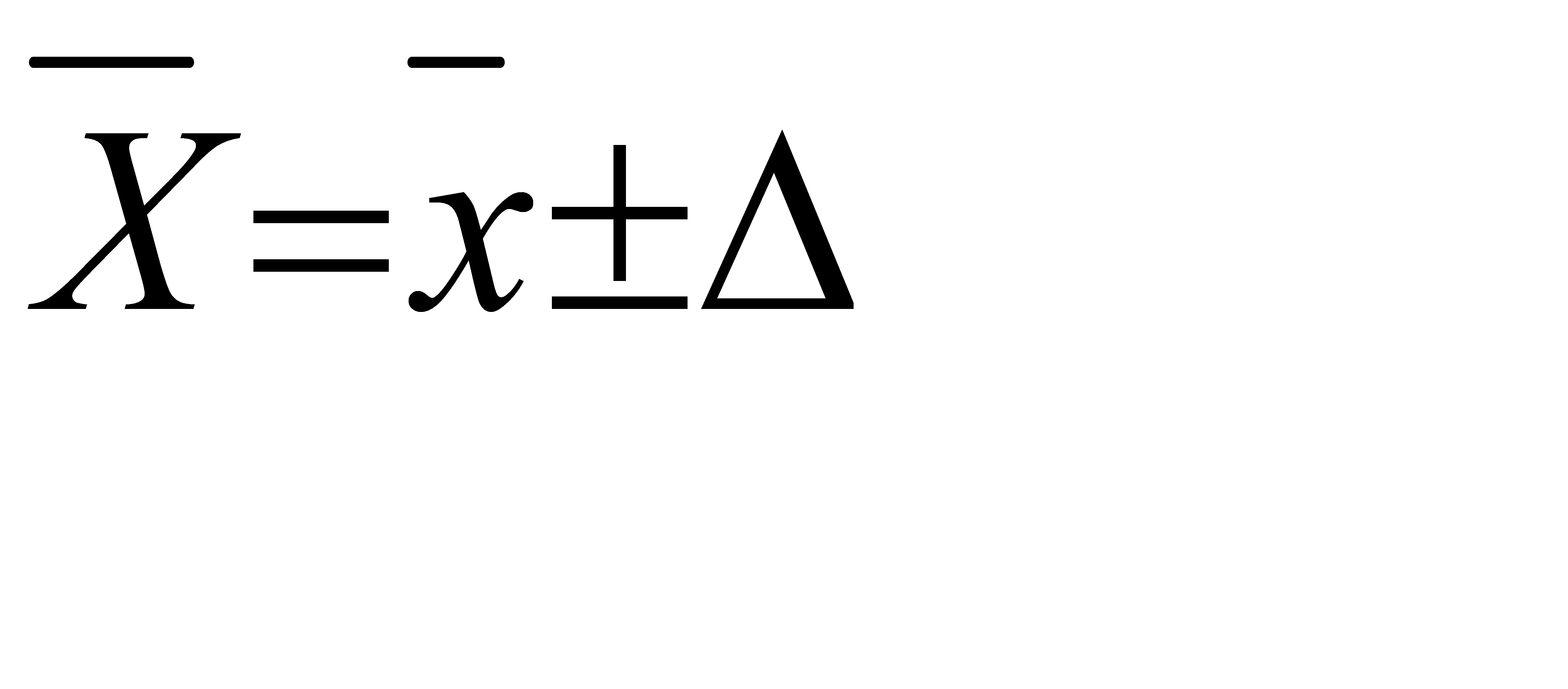, (6.12)

где 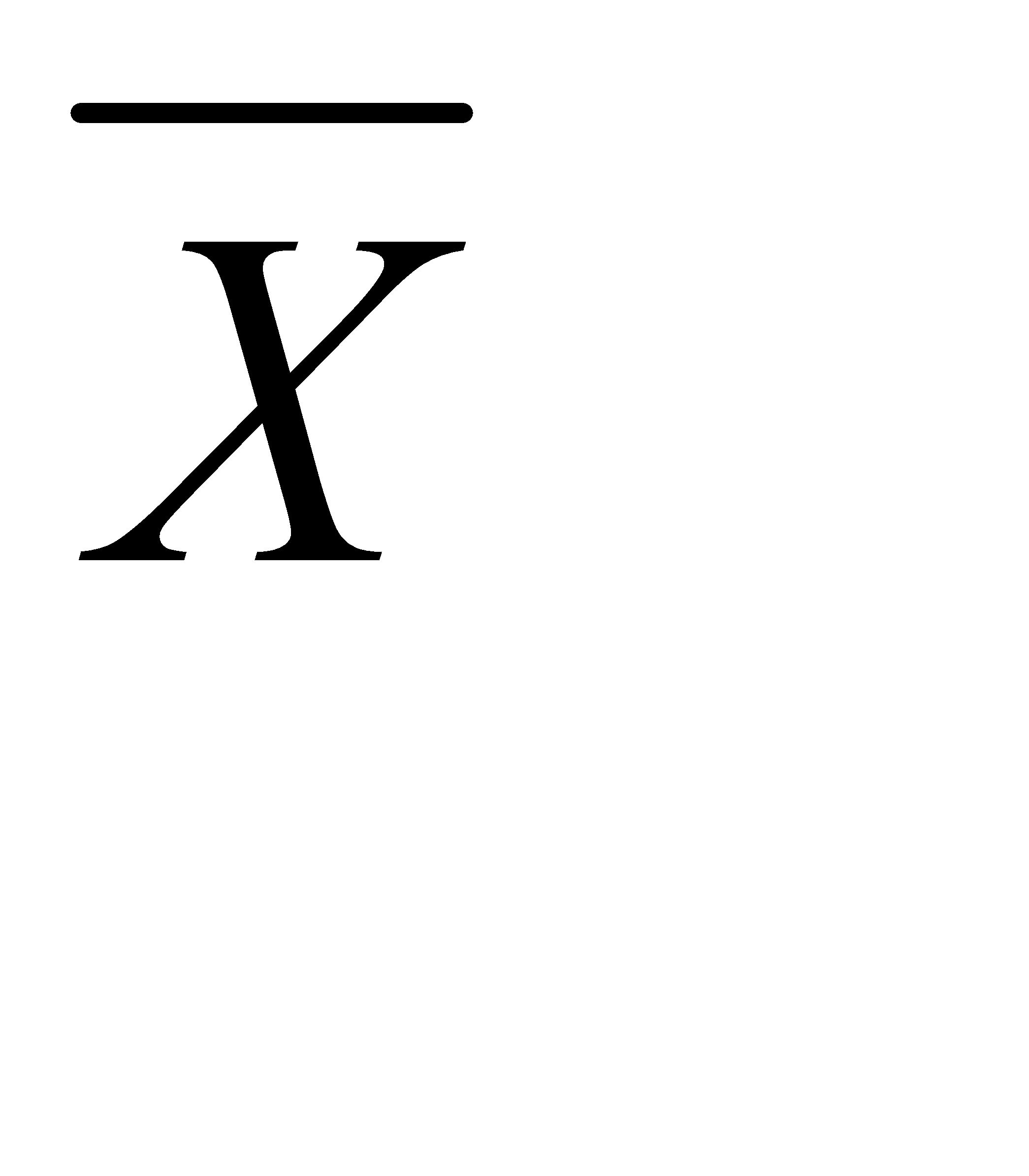– средняя в генеральной совокупности;

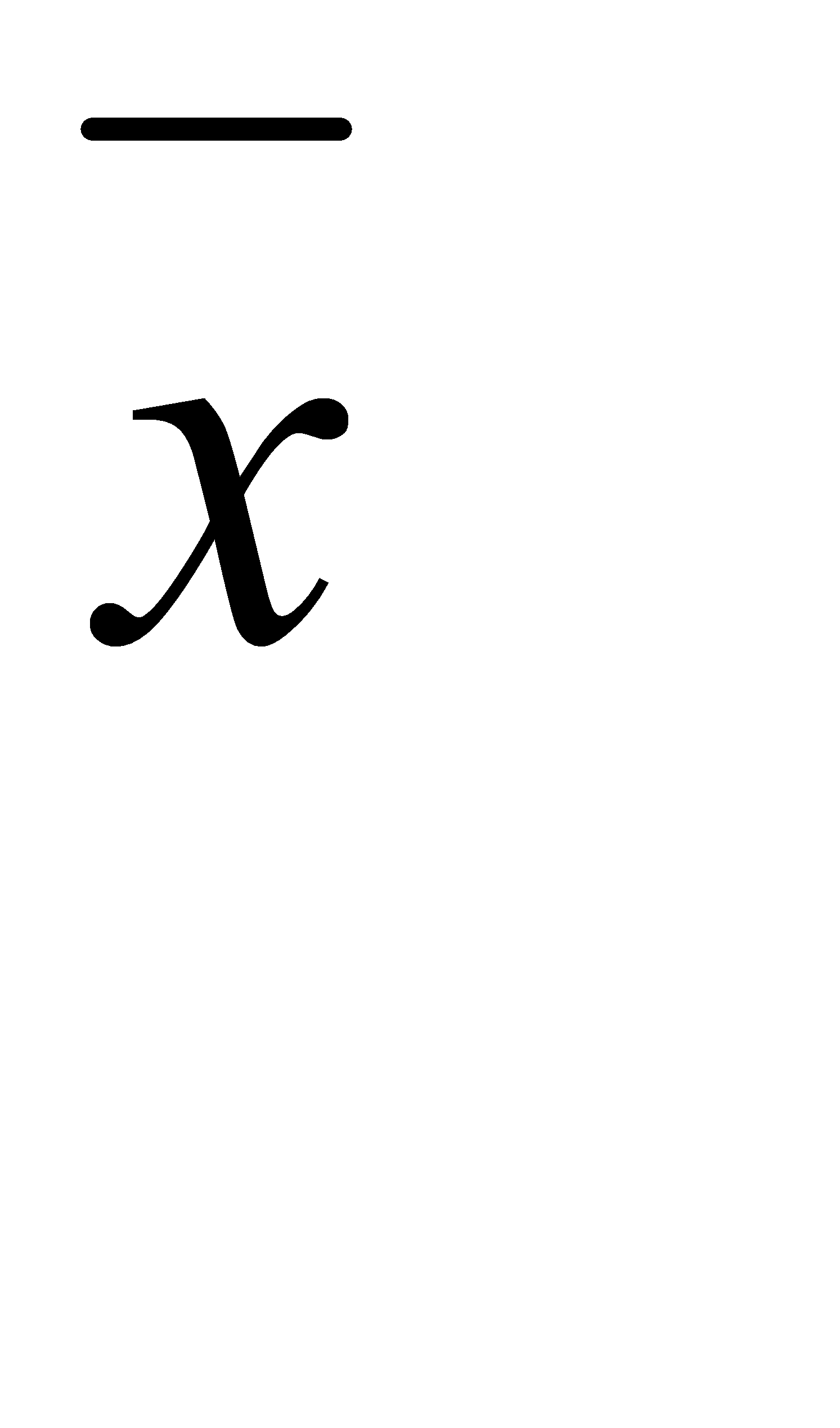– средняя в выборочной совокупности.

Для доли альтернативного признака:

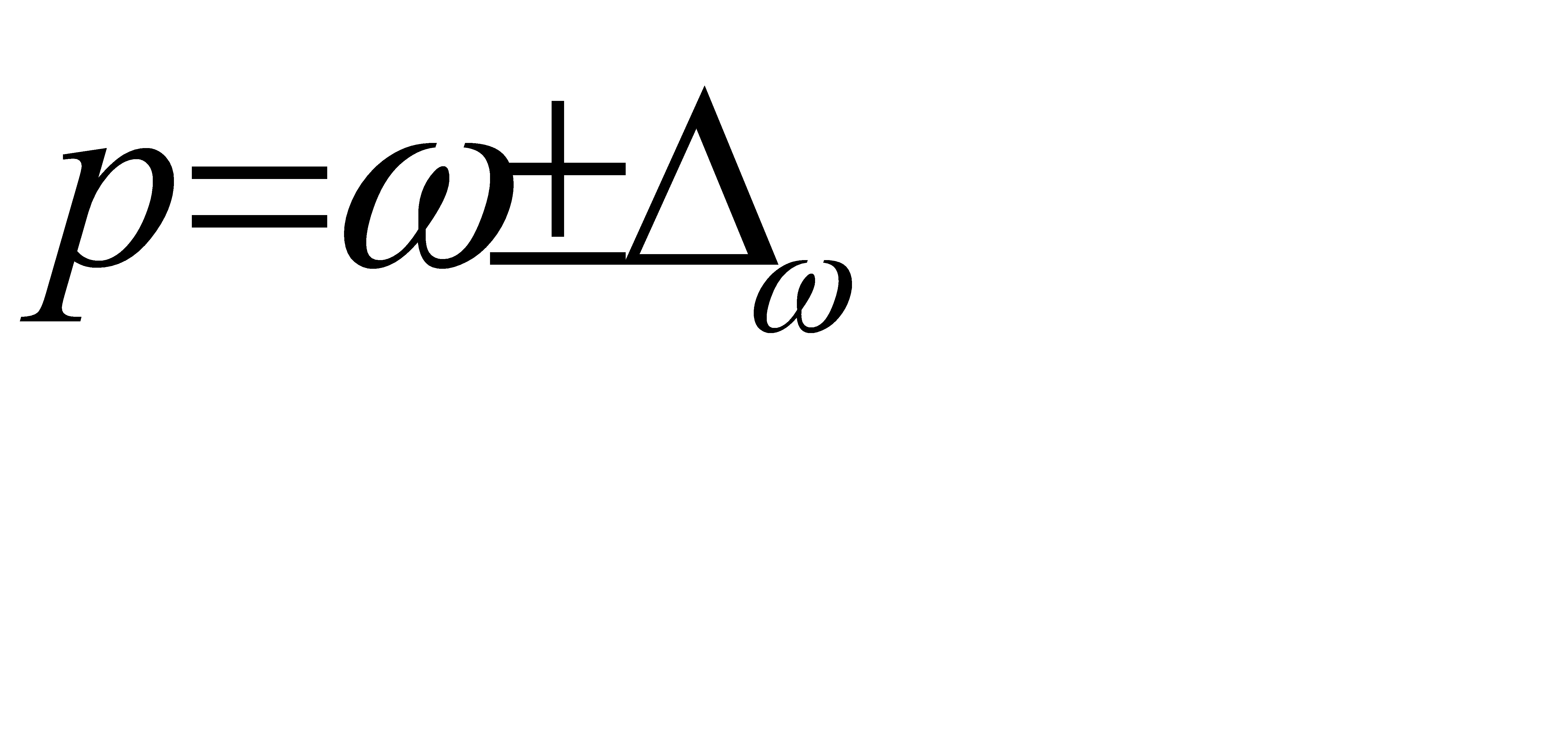. (6.13)