Сущность, значение и виды средних величин. Методы их расчета

В процессе обработки и обобщения первичных данных возникает необходимость охарактеризовать исследуемую совокупность в целом, т.е. представить все значения элементов одним характерным или типичным числом. Указанная задача решается с помощью средних величин.

Индивидуальные значения признака у отдельных единиц совокупности различны, и это различие связано с влиянием множества факторов, как общих для всех единиц совокупности, так и индивидуальных, присущих только отдельным единицам.

Например, уровень выработки рабочих определяется организационно-техническим уровнем производства, продолжительностью рабочего времени и т.д. Однако в количественном отношении выработка каждого рабочего различна, так как на нее влияют индивидуальные особенности рабочего: уровень квалификации, состояние трудовой дисциплины и т.д.

Сущность средней состоит том, что она отражает общие черты, закономерности, тенденции, присущие данной совокупности, погашая влияние индивидуальных (случайных) факторов, и поэтому является обобщающей характеристикой варьирующего признака единиц совокупности.

Средние величины широко применяются в планировании, финансово-экономическом анализе деятельности предприятий, на их основе выявляются взаимосвязи показателей и тенденции их развития. В связи с этим возникает вопрос о надежности средней величины как обобщающей характеристики совокупности.

Средняя является надежной характеристикой совокупности при условии, что совокупность качественно однородна и число единиц совокупности достаточно велико. Если же совокупность неоднородна в отношении осредняемого признака, то средняя искажает действительное положение вещей, затрудняет изучение явлений.

Все виды средних величин, используемые в статистических исследованиях, подразделяются на степенные и структурные средние.

В практической статистике наибольшее распространение получили следующие виды степенных средних: средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая.

При выборе вида степенной средней необходимо:

1. Сформулировать цель и дать понятие определяемого показателя.

2. Привести аналитическое выражение определяемого показателя.

3. Обосновать формулу расчета средней, исходя из сути явления, имеющейся информации, осмысленности результатов. Средняя используется правильно, когда получаются величины, имеющие реальный экономический смысл.

Например, при изучении закономерностей распределения используется средняя арифметическая, при изучении вариации - средняя квадратическая, при изучении интенсивности развития – средняя геометрическая.

Введем понятия и обозначения:

1.Признак, по которому находится средняя величина, называется осредняемым признаком – .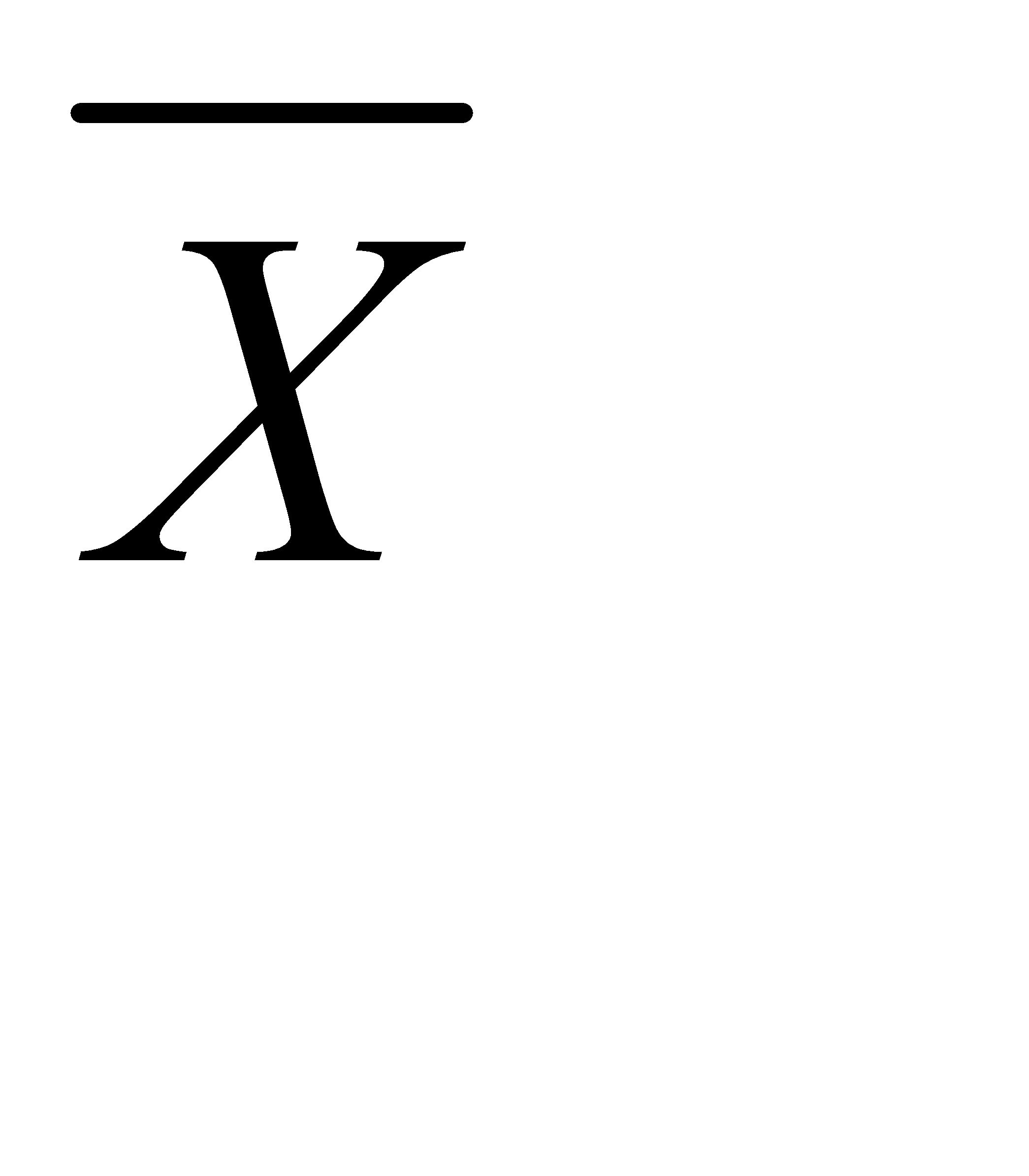

2.Величина признака у каждой единицы совокупности - индивидуальное значение (варианта) – .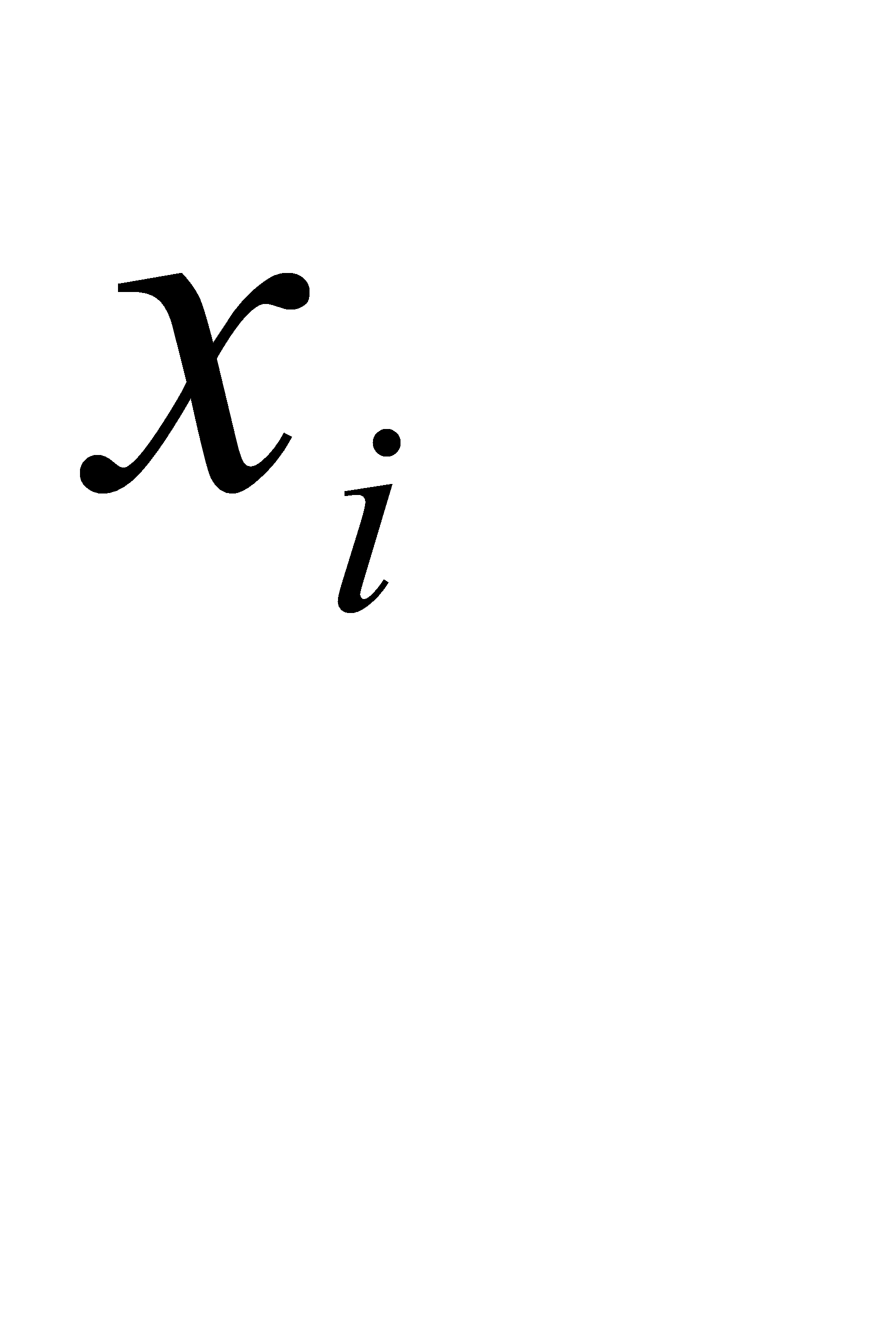

3.Повторяемость индивидуальных значений – частота (весы) – f.