Классическое определение вероятности.

Вероятностью появления события Аназывают отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов.

Обозначим число благоприятствующих событию А исходов через m, а число всех исходов-n, тогда

Р(А)= , где m-целое число; 0≤m≤n.

Пример 7.Конечной целью серии тренировок пловца является преодоления им дистанции 200м вольным стилем за время 2.17,0.

После соответствующей подготовки он проплыл эту дистанцию 25 раз. Результаты его такие:18 раз он показал желаемый результат, в остальных случаях - результат был хуже. Какова вероятность того, что в тех же условиях он преодолеет дистанцию 200м за нужное время?

Обозначим вероятность искомого случайного события буквой А.Определению подлежит вероятность Р(А).

В данном примере благоприятствующих исходов испытаний было 18, то есть m=18.Равновозможные исходы испытания - это все испытания, имевшие место в данном примере. Их число n=25.

Таким образом, вероятность искомого события находится так:

Р(А)= = =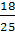0,72

Р(А)=0,72-есть числовая характеристика того, что в данном испытании спортсмен преодолеет дистанцию 200м за 2.17,0.

Свойства вероятности.

1.Вероятность достоверного события равна 1

2.Если событие невозможно, то его вероятность равна 0

3. Вероятность случайного события есть положительное число, заключенное между 0 и 1, т. е. 0≤P(А)≤1.

4. Сумма вероятности противоположных событий равна 1

P(А)+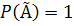

Чем больше значение вероятности внутри интервала от 0 до 1, тем более мы уверены в наступлении случайного события. Вероятность, равная 0,95, предполагает высокую степень уверенности в наступлении события. Вероятность 0,8 также предполагает высокую степень уверенности. Когда вероятность равна 0,5, то событие имеет равные шансы, как произойти, так и не произойти. Когда вероятность равна 0,2, то событие, скорее всего не произойдет. Когда вероятность равна 0,00005, то мы уверены, что событие практически не может произойти.

Лекция №2. Основные теоремы теории вероятностей.

1.Основные теоремы теории вероятности.

2.Формула полной вероятности.

3.Формула Байеса.

4.Повторение испытаний. Формула Бернулли.