Повторение испытаний. Формула Бернулли.
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Вероятность появления события в каждом испытании постоянна и равна р. Следовательно, вероятность непоявления события в каждом испытании также постоянна и равна q=1-p (как вероятность противоположного события).
Формула Бернулли определяет вероятность появления ровно k раз события А в серии из n независимых испытаний, в каждом из которых вероятность появления события А равна р:
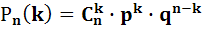
Вероятность того, что в n испытаниях событие наступит:
а) менее k раз
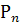 (0≤
(0≤ 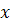 <k) =
<k) = 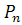 (0)+
(0)+ 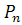 (1)+
(1)+ 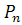 (2)+
(2)+ 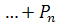 (k-1);
(k-1);
б) более k раз
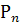 (k<
(k< 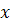 ≤n) =
≤n) = 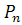 (k+1)+
(k+1)+ 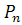 (k+2)+
(k+2)+ 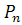 (k+3)+
(k+3)+ 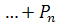 (n);
(n);
в) не менее k раз
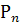 (k≤
(k≤ 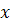 ≤n) =
≤n) = 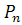 (k)+
(k)+ 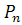 (k+1)+
(k+1)+ 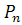 (k+2)+
(k+2)+ 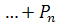 (n);
(n);
г) не более k раз
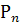 (0≤
(0≤ 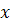 ≤k) =
≤k) = 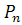 (0)+
(0)+ 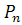 (1)+
(1)+ 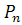 (2)+
(2)+ 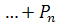 (k);
(k);
Пример 7. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничья во внимания не принимается)?
Решение. Играют равносильные шахматисты, поэтому вероятность выигрыша р =  ; следовательно, вероятность проигрыша q также равна
; следовательно, вероятность проигрыша q также равна  . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут выиграны:
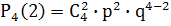 =
= 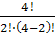
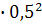
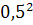 =0,375; (
=0,375; (  )
)
Найдем вероятность того, что три партии из четырех будут выиграны:
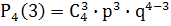 =
= 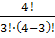
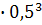
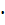
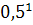 =0,3125; (
=0,3125; ( 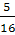 )
)
Так как 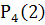 >
> 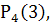 то вероятнее выиграть две партии из четырех.
то вероятнее выиграть две партии из четырех.
Дата добавления: 2016-03-10; просмотров: 1059;
