Формула полной вероятности. Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) образующих полную группу
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) 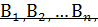 образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
Р(А)= 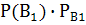 (А)+
(А)+ 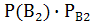 (А)+
(А)+ 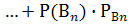 (А),
(А),
где 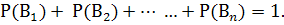
Пример 5. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Решения. Обозначим через А событие - извлечен белый шар. Возможны следующие предположения (гипотезы) о первоначальном составе шаров:
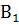 -белых шаров нет,
-белых шаров нет, 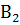 -один белый шар,
-один белый шар, 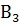 -два белых шара.
-два белых шара.
Поскольку имеется три гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице (так как они образуют полную группу), то вероятность каждой из гипотез равна  , т. е.
, т. е.
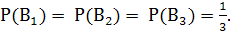
Условная вероятность того, что будет извлечен белый шар при условии, что первоначально в урне не было белых шаров, 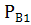 (А)=
(А)=  .
.
Условная вероятность того, что будет извлечен белый шар при условии, что первоначально в урне был один белый шар, 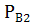 (А)=
(А)=  .
.
Условная вероятность того, что будет извлечен белый шар при условии, что первоначально в урне был о два белых шара, 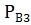 (А)=
(А)= 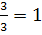 .
.
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:
Р(А)= 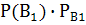 (А)+
(А)+ 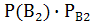 (А)+
(А)+ 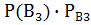 (А),
(А),
Р(А)= 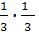 +
+ 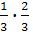 +
+ 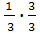 =
= 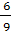 =
= 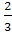
3.Формула Байеса.
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) 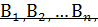 образующих полную группу. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
образующих полную группу. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
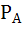 (
( 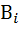 )=
)= 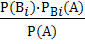 ,
,
где Р(А)= 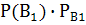 (А)+
(А)+ 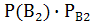 (А)+
(А)+ 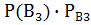 (А) формула полной вероятности .
(А) формула полной вероятности .
Пример 6. Имеется три урны с шарами. В первой урне 4 белых и 5 черных, во второй – 5 белых и 4 черных, в третьей – 6 белых шаров. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что :а) этот шар окажется белым; б)белы шар вынут из второй урны.
Решение. а) пусть А – событие, означающее, что извлечен белый шар. Рассмотрим три гипотезы:
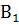 - выбрана первая урна;
- выбрана первая урна; 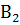 - выбрана вторая урна;
- выбрана вторая урна; 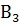 - выбрана третья урна. Так как урна, из которой извлекают шар, выбирается наугад, то
- выбрана третья урна. Так как урна, из которой извлекают шар, выбирается наугад, то
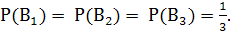
Условные вероятности события А соответственно равны:
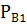 (А)=
(А)=  ;
; 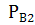 (А)=
(А)=  ;
; 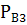 (А)=
(А)= 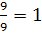 .
.
Отсюда по формуле полной вероятности получим:
Р(А)= 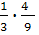 +
+ 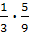 +
+ 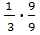 =
= 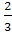
б)для определения вероятности того, что белый шар извлечен из второй урны, воспользуемся формулой Байеса:
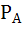 (
( 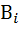 )=
)= 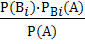 =
= 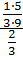 =
= 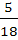
Дата добавления: 2016-03-10; просмотров: 1120;
