Правила суммы (принцип логического сложения)

Предмет изучения теории вероятностей и математической статистики.

Математические методы статистики становятся все более популярными в такой далекой от математики, чисто практической области, какой является физическая культура и спорт. Объясняется это просто: математическая статистика дает специалистам- практикантам мощный, хорошо разработанный аппарат для объективного анализа результатов педагогического, медицинского, психологического обследований и выработки практических рекомендаций по совершенствованию спортивной подготовки. Этому способствует дальнейшая математизация, современная компьютеризация.

В основе количественных спортивных изысканий лежат случайные события. Естественно поэтому предположить, что отрасль математики, изучающая случайные события и процессы, является самой подходящей для таких исследований в спорте.

Математическая статистика-это прикладная отрасль математики. Она занимается сбором исходной информации и обработкой ее в соответствии с законами теории вероятностей.

Теория вероятностей - это строгая математическая дисциплина, занимающаяся поиском закономерностей случайных событий и изучающая их.

Элементы комбинаторики

Комбинаторика-раздел дискретной математики, изучающий методы решения задач, связанных с выбором и расположением элементов дискретного множества в соответствии с заданными правилами; классическими в комбинаторике являются задачи определения числа подмножеств, различных в некотором смысле (перестановки, размещения, сочетания).

Группы, составленные из каких-либо предметов (безразлично каких, например, букв, шаров, чисел и т. п.), называются соединениями (комбинациями).

Предметы, из которых состоят соединения, называются элементами.

Различают три типа соединений: перестановки, размещения, сочетания.

Факториал

Факториал-произведение n натуральных чисел от 1до n.

Обозначается сокращенно n!=1·2·3·4·…·( n-1) · n

Например,5!=1·2·3·4·5=120

Считается, что 0!=1

Размещения

Размещениями из nэлементов по m в каждом называются такие соединения, из которых каждое содержит mэлементов, взятых из числа данных nэлементов, и которые отличаются друг от друга либо самими элементами( хотя бы одним), либо порядком их расположения.

Например, из трех элементов a,b,c можно составить три размещения по одному: a,b,c; шесть размещений по два элемента: ab, ac, bа, bс, cа, сb; шесть размещений по три элемента: abc , асb, bса, саb,сbа,bac.

Число размещений из nэлементов по mв каждом обозначается символом 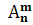и вычисляется по формуле:

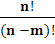= ,где 0≤ m≤ n.

Пример 1.Из 6 тренировок, идущих в последовательности 1,2,3,4,5,6,три отведены для занятий гимнастикой. Это могут быть занятия 1,2,3 или 1,4,5, или 3,4,6 и т.д. Последовательность занятий гимнастикой также имеет значение. Среди избранных трех занятий 1,2,3, это может 1,2,3 или 2,1,3, или

3,1,2 и т.д. Сколько возможно получить вариантов для образования последовательности трех занятий гимнастикой с перестановкой их из 3 возможных?

Для определения количество вариантов находим число размещений из 6 по 3

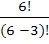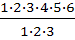= = = =120

Пример 2. Тренеры сборной команды страны по спортивной стрельбе отбирают из 10 кандидатов 4 человек на участие в предстоящем Кубке Мира(все 10 кандидатов имеют равные шансы).Сколько всевозможных групп по 4 человек можно составить из 10 кандидатов?

Для определения количества всевозможных групп находим число размещений из 10 по 4.

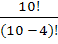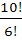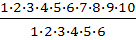= = = =5040

Перестановки

Перестановками из nэлементов называются такие соединения, из которых каждая содержит все n элементы и которые отличаются друг от друга лишь порядком расположения элементов

Например ,число перестановок из 3 элементов a,b,c равно шести:a b c, a c b, b a c, b c a, c a b, c b a.

Число перестановок из n элементов обозначается символом 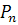и вычисляется по формуле

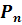=n!

Пример 3

Сколькими способами могут быть расположены 6 игроков на волейбольном поле.

Общее количество игроков 6.Находим число перестановок

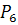=6!=720

Пример 4. Жребий определяет последовательность выступлений 10 спортсменов. Сколько вообще возможно способов в последовательности их выступлений?

Общее количество спортсменов 10. Число перестановок находим по формуле

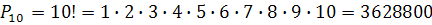
Сочетания

Сочетаниями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга, по крайней мере, одним элементом.

Например, из трех элементов a,b,c можно составить три сочетания по одному элементу: a,b,c, три сочетания по два элемента:a b, a c, b,c и одно сочетание по три элемента: a b c.

Число сочетаний из n элементов по m в каждом вычисляется по формуле

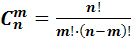,где 0≤m≤n.

Свойства сочетаний:

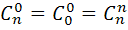1. =1

2.

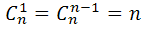
Пример 5. Для упражнения с мячом необходимо отобрать три мяча из пяти имеющихся. Сколько возможных вариантов такого отбора?

Для определения количества вариантов необходимо найти число сочетаний три из пяти

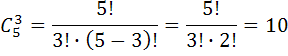
Пример 6. В полуфинале первенство России по шахматам участвуют 20 шахматистов, а в финал из них попадут только 3. При этом участнику безразлично, какое из первых мест им будет занято. Требуется установить, сколькими способами может образоваться финальная тройка.

Для определения количества способов необходимо найти число сочетаний из 20 по 3

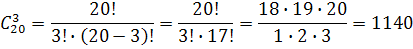
На основании этих задач можно сформулировать основные правила комбинаторики.

Правила суммы (принцип логического сложения)

Если объект a может быть выбран mспособами, а объект b может быть выбран другими n способами (не такими, как а), то выбор одного элемента a или b из объединенной совокупности может быть осуществлен m+n способами.