Основные теоремы теории вероятностей

К ним относятся теоремы сложения и умножения.

Суммой событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А и В (т.е. сумма эквивалентна союзу «или»).

Произведением двух событий А и В называется событие С, состоящее в совместном появлении А и В.

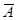называется противо­положным событию А, если оно происходит только тогда, когда не происходит А.

Теорема сложения для несовместных событий.

Вероятность суммы двух несовместных событий равна сумме их вероятностей.

P(A + B) = P(A) + P(B)

Доказательство

n – общее число исходов;

m – число исходов, благоприятных А;

k – число исходов, благоприятных B.

m и k не пересекаются, т.к. события несовместны.

m + k – число исходов, благоприятных A + B.

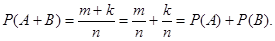
Теорема сложения для совместных событий.

P(A + B) = P(A) + P(B) – P(AB)

Доказательство

m ~ A (m благоприятно A)

k ~ B (k благоприятно B)

l ~ AB

m и k – l ~ A + B

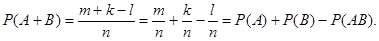
пример. Какова вероятность из набора шахматных фигур случайным образом извлечь белую фигуру или слона.

Решение

А – белая фигура; В – слон; А, В – совместно.

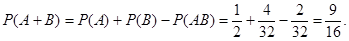
Теорема умножения событий

Событие А называется независимым от события В, если вероятность А не зависит от того произошло В или нет.

пример. В урне 7 белых и 3 черных шара. Последовательно по одному извлекаются два шара.

А – первый шар белый;

В – второй шар белый.

1) А – произошло, 6 белых и 3 черных осталось.

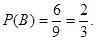
Если А не произошло, 7 белых и 2 черных шара.

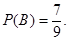
А и В зависят.

Вероятность события А при условии, что В уже произошло называется условной вероятностью А и обозначается P_B(A) = P(A/B).