Относительной частотой ω события А в n испытаниях называется отношение числа испытаний, в которых событие произошло, к n.
ВЕРОЯТНОСТЬ СОБЫТИЙ
Событие называется случайным, если в результате некоторого опыта оно может произойти и может не произойти.
Событие называется достоверным, если оно наступает обязательно в результате опыта или, возможно, что оно никогда не наступает.
События образуют полную группу, если в результате опыта наступает хотя бы одно из них.
События называются несовместными, если они не могут произойти одновременно.
События называется равновозможными, если при большом количестве испытаний они происходят одинаково часто.
Несовместное равновозможное образующее полную группу событие называется исходом опыта.
Исходы, в результате которых наступает событие называются благоприятными этому событию.
Классическое определение вероятности.
Вероятностью события P(A) называется отношение числа благоприятных этому событию исходов m к общему числу исходов n
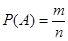
пример. В урне находятся 3 белых и 7 черных шаров. Найти вероятность, что вынутый шар окажется черным.
Решение
А – шар черный
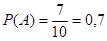 – вероятность событий.
– вероятность событий.
Утверждение: Вероятность событий 0 ≤ P(A) ≤ 1.
Если А – невозможное событие Þ P(A) = 0.
А – достоверное событие Þ P(A) = 1.
пример. Партия готовой продукции из n одинаковых изделий содержит m бракованных. Контроллер наудачу выбирает l изделий. Какова вероятность, что среди них окажется k бракованных.
Решение
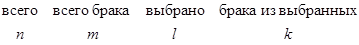
Событие А – k бракованных из l выбранных: 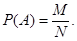
Общее число исходов: 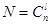
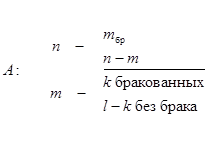
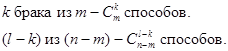
По правилу умножения: 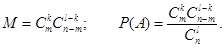
Относительной частотой ω события А в n испытаниях называется отношение числа испытаний, в которых событие произошло, к n.
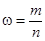
Частотное определение вероятности 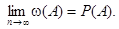
Геометрическое определение вероятности 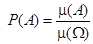
μ – мера (длина, площадь, объем).
А – множество, соответствующее наступлению исходов, благоприятных событию А.
Ω – множество всех исходов.
пример. Заданы два натуральных числа от 1 до 10 x, y Î [1; 10].
Какова вероятность, что их произведение меньше 4х xy < 4.
Решение
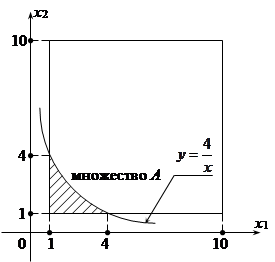
Дата добавления: 2016-02-27; просмотров: 769;
