Центральная предельная теорема (ЦПТ)
Центральная предельная теорема теории вероятностей (теорема
Ляпунова) устанавливает условие, при котором предельный закон распределения суммы 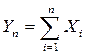 , когда число слагаемых неограниченно возрастает является нормальным.
, когда число слагаемых неограниченно возрастает является нормальным.
Сформулируем и докажем простейшую форму ЦПТ, когда СВ Х1,Х2, …, Хn взаимно независимы и одинаково распределены.
Теорема. Если СВ Х1, Х2, …, Хn взаимно независимы и имеют один и тот же закон распределения с МОЖ m и дисперсией  , то при неограниченном увеличении n закон распределения суммы
, то при неограниченном увеличении n закон распределения суммы 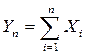 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
Для доказательства этой теоремы А.М. Ляпунов в 1900 г. создал специальный метод характеристических функций.
Характеристической функцией СВ Х называется функция  .
.
Где j – мнимая единица.
Зная закон распределения СВ Х можно найти ее ХФ.
Для дискретной СВ Х с плотностью распределения
| Хк | Х1 | Х2 | … | Хn |
| Рк | Р1 | Р2 | … | Рn |
ХФ  ,
,
Для непрерывной СВ Х с плотностью распределения f(x) ХФ
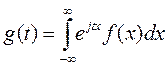 .
.
Как видно из формулы ХФ 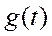 является преобразованием Фурье соответствующей ей плотности распределения
является преобразованием Фурье соответствующей ей плотности распределения 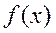 . Из теории преобразований Фурье известно, что
. Из теории преобразований Фурье известно, что  может быть определенна путем обратного преобразования Фурье.
может быть определенна путем обратного преобразования Фурье.

Свойство 1. ХФ 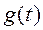 вещественна тогда и только тогда, когда соответствующая плотность распределения
вещественна тогда и только тогда, когда соответствующая плотность распределения  является четной функцией. При этом сама функция
является четной функцией. При этом сама функция 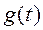 является также четной.
является также четной.
Справедливость этого свойства следует из свойств преобразований Фурье.
Свойство 2. Если случайные величины Х и Y связанны соотношением Y=aX, где a – неслучайный множитель, то их ХФ связанны соотношением
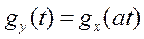 .
.
Доказательство: 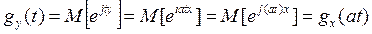
Свойство 3. ХФ суммы независимых СВ равна произведению ХФ слагаемых.
Доказательство: Х1, Х2, …, Хn – независимые СВ, имеющие соответственно ХФ gХ1(t), gХ2(t), …, gХn(t). Найдем ХФ СВ 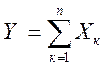 . Имеем
. Имеем 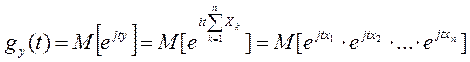
Так как Хк(к=1, 2, …, n) независимы, то независимы и функции 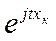 , потеореме умножения МОЖ получим
, потеореме умножения МОЖ получим
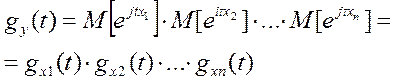
Вернемся к доказательству ЦПТ .
Т.к. СВ Х1, Х2, …, Хn имеют один и тот же закон распределения, то они имеют одну и ту же ХФ gх(t). Следовательно в силу свойства 3 ХФ 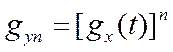
Разложим функцию gх(t) по формуле Маклорена, ограничиваясь тремя членами 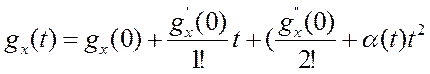
Остаточный член по форме Лагранжа имеет вид a(t)®0, при t®0.
При определении коэффициентов разложения и оценке остаточного члена a(t) положим, что СВ Хi непрерывны с плотностью распределения f(x). В таком случае 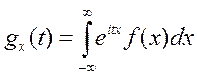 и при t=0
и при t=0 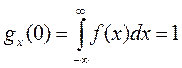
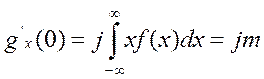 .
.
Положим, что m=0 тогда 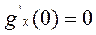
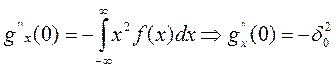
Дата добавления: 2016-03-05; просмотров: 961;
