Подставляя в формулу Маклорена получим

.

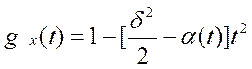Перейдем от величины Yn к другой (нормированной) СВ

.

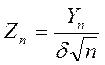Она удобна тем, что ее дисперсия не зависит от n и равна 1 при любом n.

Вместо того, чтобы доказывать, что закон распределения СВ Zn при увеличении n приближается к нормальному, покажем, что ее ХФ приближается к ХВ нормального закона.

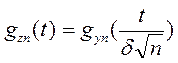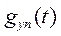, где - ХВ СВ Y_n.

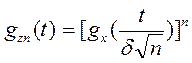или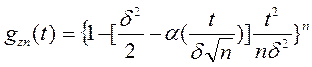

Прологарифмируем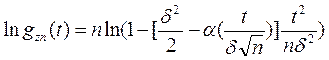

Введем обозначения 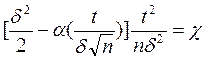, тогда .

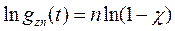Будем неограниченно увеличивать n. При этом c стремиться к 0. Разложим 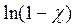в ряд и ограничимся одним числом разложения 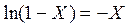, тогда получим

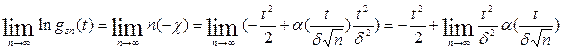По определению a(t)®0, при t®0, т.е.

.

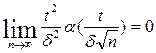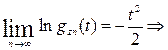
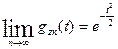
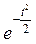- ХФ нормального закона с параметрами m=0 и d=1.

Теорема доказана.

Теорема Муавра - Лапласа.

Если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью Р, то для любого интервала (a,b) справедливо соотношение

,

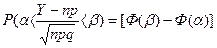где Y- число появлений события А в опытах; q=1-p

Ф(x)-функция Лапласа.

ТЕМА 6 Выборочный метод. Статистические оценки параметров распределения.

Предмет математической статистики. Генеральная совокупность и выборки.

Математической статистикой называется наука, занимающаяся разработкой методов получения, описания и обработки опытных данных с целью изучения закономерностей случайных массовых явлений.

Типичными задачами МС являются следующие:

1. Оценка на основании результатов измерений неизвестной функции распределения: в результате независимых опытов над случайной величиной 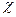получим следующие значения 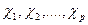. Требуется приближенно оценить 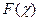СВ Х

2. Оценка неизвестных параметров распределения СВ Х имеет функцию распределения определенного вида, зависящую от 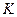параметров, значение которых неизвестно. Требуется оценить значение этих параметров.

Статистическая проверка гипотез. Одна из основных задач статистической проверки гипотез ставится так: на основании некоторых соображений можно считать, что функция распределения исследуемой СВ Х есть 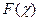. Спрашивается: совместимы ли полученные наблюдением значения с гипотезой, что СВ Х действительно имеет распределение .

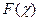В частности, если закон распределения исследуемой СВ Х не вызывает сомнений и в проверке нуждаются только значения некоторых параметров, характеризующих распределение, то в задаче спрашивается: не опровергают ли опытные данные ту гипотезу, что параметры закона распределения имеют предположенные значения.

Пусть требуется исследовать какой-нибудь признак, свойственный большой группе однотипных изделий (размер, вес и т.д.). Совокупность значений признака всех 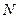изделий данного типа называется генеральной совокупностью. При этом предполагается, что число 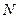в генеральной совокупности весьма велико. В некоторых случаях количество значений образующих генеральную совокупность, можно мыслить и бесконечным.

На практике сложное обследование применяется редко. Обычно случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.