После подстановки (15) в уравнение (14), получим

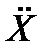+ ω²Х = 0 (16)

Выражение (16) является дифференциальным уравнением гармонических колебаний. Частным решением этого уравнения является по выбору или функция X=ASin(ωt+φ_o), или функция X=ACos(ωt+φ_o). Решением дифференциального уравнения называется такая функция, после подстановки которой в уравнение, последнее обращается в тождество. В записанных решениях величина ω – циклическая частота данного математического маятника. С учетом соотношения (15) следует, что математический маятник при малых углах отклонения совершает гармонические колебания с частотой, равной

ω= 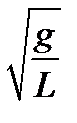, (17)

или с периодом

Т = 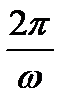= 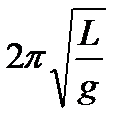(18)

Ускорение свободного падения.Закономерности движения планет и их спутников, падения тел на Землю, колебания маятников и тому подобные явления свидетельствуют о существовании сил взаимного притяжения между телами. Эти силы подчиняются закону всемирного тяготения (гравитации), установленному Ньютоном, согласно которого, между всякими двумя материальными точками действует сила F_T, прямо пропорциональная произведению масс этих точек (m₁ и m₂) и обратно пропорциональная квадрату расстояния r между ними:

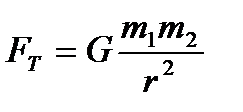.(19)

В формуле (19) коэффициент пропорциональности G = 6,67·10^-11 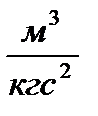одинаков для всех тел в природе и называется гравитационной постоянной или постоянной тяготения.

Сила F_Т тяготения к Земле каждого, находящегося на ней или вблизи нее тела, направлена к центру Земли и численно равна:

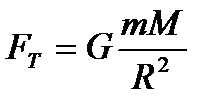, (20)

где m и М–массы тела и Земли, R–расстояние от центра тяжести тела до центра Земли.

Любое взаимодействие между реальными телами осуществляется через то или иное физическое поле. Гравитационное взаимодействие осуществляется посредством гравитационного поля. Это поле проявляет себя в том, что на помещенное в него другое тело действует сила тяготения (гравитации). Гравитационное поле характеризуется двумя важными величинами – напряженностью 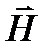и потенциалом гравитационного поля .

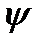Напряженность гравитационного поля – это силовая характеристика поля, векторная величина, показывающая, какая сила в данной точке поля действует на тело единичной массы 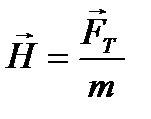, где m масса тела, находящегося в данной точке поля. Если пренебречь центробежной силой инерции, обусловленной суточным вращением Земли, то вблизи земной поверхности напряженность гравитационного поля можно считать равной по величине и направлению ускорению свободного падения т.е. 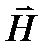= 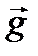. Потенциал гравитационного поля – это энергетическая характеристика поля, скалярная величина, определяющая потенциальную энергию единичной массы тела, находящегося в данной точке гравитационного поля .

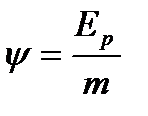Одним из проявлений силы всемирного тяготения является сила тяжести. Движение тела под действием только одной силы тяжести называютсвободным падением,а ускорение, приобретаемое телом под действием этой силы, называется ускорением свободного падения.

Ускорение свободного падения в данной точке пространства одинаково для всех тел и не зависит ни от материала тела, ни от его размеров. Сила тяжести, как и сила гравитации, обратно пропорциональна квадрату расстояния R² от центра Земли до центра тяжести тела. Кроме того, не шарообразность формы Земли (ее форма представляет эллипсоид вращения, или сфероид), а также действие на тела центробежной силы инерции за счет суточного вращения Земли, приводит к зависимости ускорения свободного падения, а следовательно и силы тяжести, от географической широты места. Вблизи земной поверхности максимальное ускорение имеют тела на полюсах (9,83 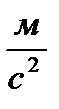) и минимальное на экваторе (9,78 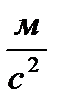). На широте 45^о оно равно 9,80665 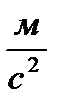и называется «стандартным ускорением».

Рабочая формула.Соотношение (18) можно использовать для опытного определения ускорения свободного падения g. После возведения в квадрат уравнения (18), получим выражение для расчета ускорения свободного падения:

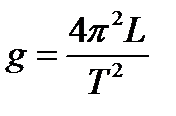(21)

Расчет ускорения g можно произвести двумя способами. Первый – это непосредственно по формуле (21), подставив в нее L и T. Второй – графический. Для этого способа необходимо измерить период колебаний Т при различных длинах нити L, а затем построить график зависимости 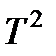от L. Получится (следует из уравнения (21)) прямая линия с коэффициентом наклона 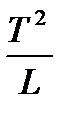= 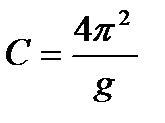. Определяя наклон C из экспериментального графика (рис. 6), можно рассчитывать величину g по формуле: 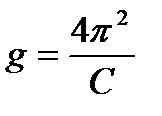(22).

Описание установки.Внешний вид экспериментальной установки показан на рис.5. На леске, закрепленной на кронштейне стойки штатива, подвешен стальной шарик. Длина (высота) стойки штатива 1250 мм. Для нахождения периода колебаний маятника используется световой барьер. При выполнении работы подключите источник питания к световому барьеру и установите переключатель на световом барьере в положение:

Рис5. Математический маятник.