Зависимые и независимые случайные величины.
Определение. Распределение одной СВ, входящей в систему, найденное при условии, что другая СВ, входящая в систему, называется условным законом распределения.
F(x/y)= 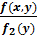 ;
; 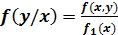
Используя оба соотношения можно записать:
f(x,y)=f1(x)f(y/x)=f2(y)f(x/y) – называют теоремой умножения распределения.
Для независимых СВ
f(x/y)=f1(x); f(y/x)=f2(y).
Таким образом СВ Х и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае СВ X и Y называются зависимыми.
Теорема. Для того, чтобы непрерывные СВX и Y были независимыми, необходимо и достаточно, чтобы плотность распределения системы(X, Y) была равна произведению плотностей распределения отдельных величин, входящих в систему
f(x,y)=f1(x)f2(y).
доказательство: необходимость :пусть X и Y – независимы СВ, тогда f(x/y)=f1(x); f(y/x)=f2(y) и следовательно f(x/y)=f1(x)fdx.
достаточность: пусть f(x,y)=f1(x)f2(y). Отсюда, получаем
f1(x)= 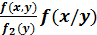 ;
; 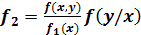
Следствие. Если плотность распределенияf(x,y) представлена в виде произведения двух сомножителей, первый из которых содержит только X, а второй только Y, то случайные величины X и Y – независимы.
3. Числовые характеристики системы двух СВ. Корреляционный момент. Коэффициент корреляции.
На практике наиболее употребительными являются следующие числовые характеристики СВ
начальные моменты первого порядка:
 a10=M[X1Y0]=M[X]=mx
a10=M[X1Y0]=M[X]=mx
a01=M[X0Y1]=M[Y]=my ,которые являются МОЖ СВ X и Y,
входящие в систему
Dx=µ20=[(X-mx)2(Y-my)0]=M[(X-mx)2]
Dy= µ 02=[(X-mx)0(Y-my)2]=M[(Y-my)2].
Особую роль при исследовании системы двух СВ играет второй смешанный центральный момент µ11, который называется корреляционным моментом или моментом связи kx,y .
kx, y= µ11=M[(X-mx)(Y-my)]
для оценки степени взаимного влияния двух СВ обычно используют не сам момент связи kx,y, а безразмерное отношение
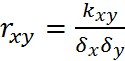 ,
,
которое называют коэффициентом корреляции СВ X и Y.
Свойство 1. Если случайные величины X и Y независимы, то корреляционный момент и коэффициент корреляции равны нулю.
Дата добавления: 2016-03-05; просмотров: 908;
