Зависимые и независимые случайные величины. Понятие «зависимость» случайных величин в теории вероятностей отличается от понятия функциональной зависимости
Понятие «зависимость» случайных величин в теории вероятностей отличается от понятия функциональной зависимости. Если случайная величина X находится в вероятностной зависимости от случайной величины Y, то это означает, что с изменением величины Y случайная величина X имеет тенденцию к изменению. В ряде случаев вероятностная зависимость бывает настолько слаба, что ею пренебрегают, в других же случаях, наоборот, зависимость между величинами настолько тесная, что, зная значения одной из них, можно указать значения другой.
Случайная величина X, входящая в систему (X, Y) является независимой от случайной величины Y, если ее закон распределения не зависит от того, какое частное значение приняла случайная величина Y.
Для случайных непрерывных величин условие независимости случайной величины X от Y записывается в виде
 при любом y. Это означает, что у этих распределений одинаковая форма кривых и одинаковые параметры.
при любом y. Это означает, что у этих распределений одинаковая форма кривых и одинаковые параметры.
Случайная величина X, входящая в систему (X, Y) является зависимой от случайной величины Y, если ее закон распределения зависит от того, какое частное значение приняла случайная величина Y.
Условие же зависимости случайной величины X от Y записывается в виде
 ,
,
что означает или несоответствие форм кривых распределения или неравенство параметров.
Теорема. Зависимость и независимость случайных величин, входящих в систему, всегда взаимна, т.е., если величина X не зависит от Y, то и величина Y не зависит от X.
Рекомендуется доказать теорему о взаимностизависимости и независимости случайных величин X и Y самостоятельно ввиду простоты.
Для случайных дискретных величин условие независимости случайной величины X от Y определяется равенством безусловной и условной вероятностей друг другу
 ,
,
а условие зависимости – неравенством их, т.е.
 .
.
Пример 4. В условиях примера 3 определить зависимость или независимость случайных величин X и Y.
Решение.
Так как 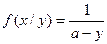 , а
, а 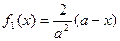 , то
, то  , что указывает на зависимость случайных величин X и Y.
, что указывает на зависимость случайных величин X и Y.
В связи с тем, что из равенства 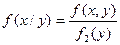 следует равенство
следует равенство
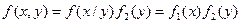 , поскольку
, поскольку  , то выражение
, то выражение

называют условием независимости случайных величин.
Дата добавления: 2016-04-19; просмотров: 1399;
