Числовые характеристики системы двух случайных величин
В качестве числовых характеристик системы случайных величин принимают начальные и центральные моменты системы.
Начальные моменты системы.
Начальным моментом 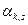 порядка k, s системы (X, Y) называют математическое ожидание произведения
порядка k, s системы (X, Y) называют математическое ожидание произведения 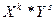 .
.
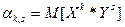 .
.
Для системы случайных дискретных величин
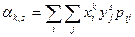 ,
,
где 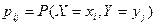 - вероятность того, что система (X, Y) примет значение
- вероятность того, что система (X, Y) примет значение 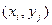 , а суммирование распространяется по всем возможным значениям случайных величин X и Y.
, а суммирование распространяется по всем возможным значениям случайных величин X и Y.
Для системы случайных непрерывных величин
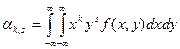 ,
,
где f(x, y) – плотность распределения системы (X, Y).
На практике чаще всего применяются начальные моменты первого порядка:
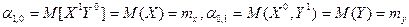 .
.
Они являются математическими ожиданиями случайных величин X и Y, входящих в систему и характеризуют положение системы, представляя собой координаты средней точки (центра рассеивания) системы на плоскости.
На основе определения начальных моментов можно записать формулы для математических ожиданий M(X) и M(Y) случайных величин X и Y, входящих в систему, в случае:
а) дискретных величин
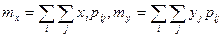 ,
,
б) непрерывных величин
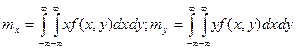 .
.
Пример 5. Система двух случайных дискретных величин задана таблицей распределения:
| X1=3 | X2=6 | X3=9 | |
| Y1=4 | 0,1 | 0,2 | 0,3 |
| Y2=8 | 0,2 | 0,1 | 0,1 |
Найти математическое ожидание случайных величин X и Y, входящих в систему.
Решение.
 ;
;
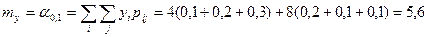 .
.
Вывод: центр группирования этой системы случайных величин находится в точке с координатами 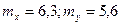 .
.
Центральные моменты системы.
Центральным моментом системы (X, Y) порядка k, s называют математическое ожидание произведения 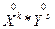 :
:
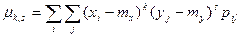 для дискретных величин и
для дискретных величин и
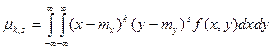 для непрерывных величин.
для непрерывных величин.
Среди центральных моментов большое практическое значение имеют вторые центральные моменты системы:
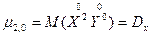 и
и 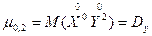 .
.
Эти моменты являются дисперсиями случайных величин X и Y, входящих в систему, и характеризуют рассеивание случайных точек в направлении осей 0x и 0y.
Формулы дисперсий случайных величин X и Y, входящих в систему,
а) для дискретных величин:
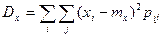 ;
;  ,
,
б) для непрерывных величин:
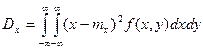 ;
; 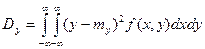 .
.
Для характеристики системы случайных величин важную роль играет второй смешанный центральный момент
 ,
,
т.е. математическое ожидание произведения центрированных величин.
Эта характеристика называется корреляционным моментомили ковариацией:
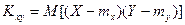 .
.
Корреляционный момент кроме рассеяния случайных величин X и Y характеризует еще и связь их между собой.
Корреляционный момент вычисляется по формуле:
а) для системы дискретных величин
 ;
;
б) для системы непрерывных величин
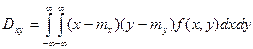 .
.
При решении многих задач, в которых требуется определить корреляционный момент, удобнее пользоваться следующей формулой:
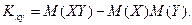
Она вытекает из определения корреляционного момента.
Определение.Случайные величины являются связанными между собой, если при изменении одной из них другая реагирует изменением своего условного математического ожидания.
Условное математическое ожидание случайной непрерывной величины можно определить по формуле
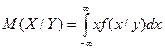 ,
,
где M(X/Y) - условное математическое ожидание случайной величины X при условии, что случайная величина Y приняла частное значение y.
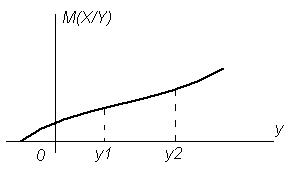
Рисунок 3.9 Графическая интерпретация условного математического ожидания M(X/Y)
Условное математическое ожидание M(X/Y) является функцией случайной величины Y (рис. 3.9). Если 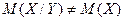 , то случайные величины X и Y считаются связанными. Связанность случайных величин является частным случаем их зависимости.
, то случайные величины X и Y считаются связанными. Связанность случайных величин является частным случаем их зависимости.
На практике чаще всего M(X/Y) имеет вид прямой линии, которую называют линией регрессии, описываемой уравнением
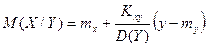 .
.
Положение линии регрессии зависит от величины и знака корреляционного момента (рис. 3.10). Если значение корреляционного момента случайных величин X и Y меньше нуля, то регрессия отрицательная, а если значение корреляционного момента больше нуля, то регрессия положительная. Если значение корреляционного момента равно нулю, то случайные величины X и Y между собой не связаны.
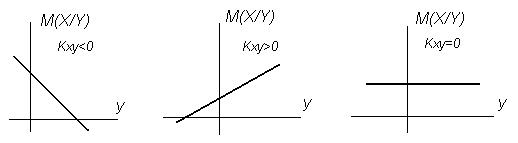
Рисунок 3.10 Положение линии регрессии в зависимости от величины и знака корреляционного момента
Свойства корреляционного момента:
а) 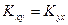 ;
;
б) 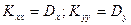 ;
;
в)  - корреляционная матрица.
- корреляционная матрица.
Для системы двух случайных величин числовыми характеристиками являются: 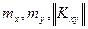 .
.
Из определения корреляционного момента следует, что размерность его равна размерности произведения случайных величин X и Y. Поэтому для одних и тех же величин значения его будут зависеть от единиц измерения случайных величин.
Эта особенность корреляционного момента является его недостатком, так как вызывает затруднения при сравнении корреляционных моментов различных пар случайных величин. Для устранения этого недостатка вводят новую числовую характеристику – коэффициент корреляции или нормированный корреляционный момент.
Коэффициентом корреляции 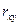 случайных величин X и Y называют отношение корреляционного момента
случайных величин X и Y называют отношение корреляционного момента 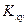 к произведению средне – квадратичных отклонений этих величин:
к произведению средне – квадратичных отклонений этих величин:
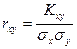 .
.
Для независимых величин 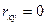 ; для величин, связанных между собой линейной зависимостью,
; для величин, связанных между собой линейной зависимостью, 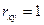 или
или 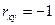 . Равенство нулю коэффициента корреляции еще не свидетельствует о том, что случайные величины являются независимыми.
. Равенство нулю коэффициента корреляции еще не свидетельствует о том, что случайные величины являются независимыми.
Система произвольного числа случайных величин. В тех случаях, когда изучаются процессы с относительно большим числом n случайных переменных 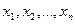 целесообразно пользоваться корреляционной матрицей:
целесообразно пользоваться корреляционной матрицей:
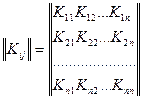 ,
,
где 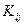 представляет собой корреляцию (смешанный момент второго порядка) между величинами
представляет собой корреляцию (смешанный момент второго порядка) между величинами 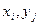 .
.
К числовым характеристикам системы n случайных переменных относят их математические ожидания и корреляционную матрицу. Математические ожидания определяют положение центра группирования системы, а корреляционная матрица характеризует разброс или рассеяние случайных точек около центра группирования и попарную связанность случайных величин. Если случайные величины будут не коррелированны между собой, то эта матрица будет иметь нули везде кроме диагонали.
Вопросы для повторения
1 Что называется системой двух случайных величин? Приведите примеры.
2 Что понимают под функцией распределения системы двух случайных величин? Какими свойствами она обладает?
3 Как определяется вероятность попадания случайной точки заданную область, если известна функция распределения системы двух случайных величин?
4 Что называется плотностью распределения системы двух непрерывных случайных величин? Каковы ее свойства?
5 По каким формулам определяются плотности распределений составляющих системы?
6 Что понимают под условным законом распределения случайной величины?
7 Какая связь между плотностью распределения системы, условной плотностью и плотностью составляющей системы?
8 Сформулируйте теоремы, устанавливающие необходимые и достаточные условия независимости случайных величин.
9 Что собой представляют начальные моменты первого порядка и как они рассчитываются?
10 Что собой представляют вторые центральные моменты и как они рассчитываются?
11 Корреляционный момент системы двух случайных величин и его свойства.
12 Что понимают под условным математическим ожиданием?
13 Чем отличается коэффициент корреляции от корреляционного момента?
14 Как по коэффициенту корреляции установить степень связанности случайных величин, входящих в систему?
15 Какими числовыми характеристиками характеризуется система n случайных величин?
Упражнения
3.1 Система случайных величин (x,y) задана рядом распределения. Определите вероятность того, что случайная величина x примет значение равное двум, т.е. P(x=2).
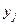 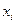
| |||
| 0,1 | 0,2 | 0,1 | |
| 0,2 | 0,3 | 0,1 |
3.2 Значения числовых характеристик системы случайных величин X и Y 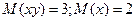 ;
; 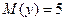 . Требуется рассчитать корреляционный момент.
. Требуется рассчитать корреляционный момент.
3.3 Система случайных величин (X,Y) задана рядом распределения. Определите М (X) и М(y):
| yi xi | |||
| 0.1 | 0.2 | 0.1 | |
| 0.2 | 0.3 | 0.1 |
3.4 Плотность совместного распределения системы двух случайных величин (X,Y)
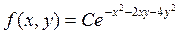 .
.
Найти: а) постоянный множитель C; б) плотности распределения составляющих; в) условные плотности распределения составляющих.
3.5 При каком значении коэффициента корреляции функция условного математического ожидания M(X/Y) отображается прямой, параллельной оси абсцисс?
Дата добавления: 2016-04-19; просмотров: 1405;
