Закон распределения системы случайных дискретных величин
Пусть имеется система случайных величин (X, Y) , закон распределения которой задан таблицей 3.1.
Таблица 3.1
| Xi Y j | Y1 | Y2 | … | Y j | … | Y m |
| X1 | p(x1,y1) | p(x1,y2) | p(x1,yj) | p(x1,ym) | ||
| X2 | p(x2,y1) | p(x2,y2) | p(x2,yj) | p(x2,ym) | ||
| ... | ||||||
| X i | p(xi,y1) | p(xi,y2) | p(xi,yj) | p(xi,yj) | ||
| … | ||||||
| X n | p(xn,y1) | p(xn,y2) | p(xn,yj) | p(xn,ym) |
В ячейках таблицы расположены вероятности того, что случайные величины X и Y примут i – тое и j – тое частные значения, т.е.
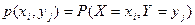 .
.
Для получения закона распределения случайной величины, входящей в систему пользуются формулами:
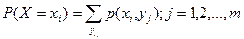 ,
, 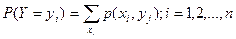 .
.
Пример 2. Дана система случайных величин (X, Y), закон распределения которой задан таблицей 3.2.
Таблица 3.2
| X1=1 | X2=2 | X3=3 | |
| Y1=2 | 0,1 | 0,2 | 0,1 |
| Y2=4 | 0,2 | 0,3 | 0,1 |
Требуется определить законы распределения случайных величин X и Y.
Решение.
Определяем вероятности того, что случайная величина X случайная величина примет значения 1;2;3, а случайная величина Y - значения 2;4:
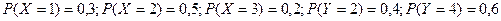 .
.
Производим проверку суммированием вероятностей, которая должна быть равна единице по каждой случайной величине, т.е.
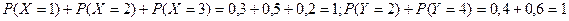 .
.
Следовательно, законы распределения случайных величин X и Y определены правильно.
Дата добавления: 2016-04-19; просмотров: 1217;
