Плотность распределения системы двух случайных величин
Закон распределения системы двух случайных дискретных величин может быть задан либо в виде графика, либо в виде таблицы с двумя входами, либо функцией распределения.
Для задания закона распределения системы двух случайных непрерывных величин на практике пользуются не функцией распределения, а плотностью распределения, так как она более удобна при вычислениях.
Здесь и далее будем предполагать, что функция распределения имеет всюду непрерывную частную производную.
Плотностью распределения (дифференциальной функцией распределения) f(x, y) системы двух случайных величин (X, Y) называется вторая смешанная частная производная от функции распределения:
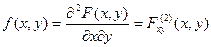 .
.
Иначе говоря, плотность распределения системы двух случайных величин (X, Y) представляет собой предел отношения вероятности попадания случайной точки (X, Y) в элементарный прямоугольник к площади этого прямоугольника, когда оба размера его стремятся к нулю (рис. 3.5).
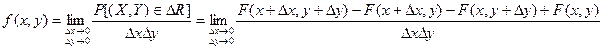 .
.
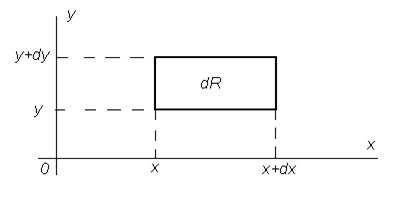
Рисунок 3.5 Вероятность попадания случайной точки (X, Y) в элементарный прямоугольник
Геометрически функция f(x, y) представляет собой некоторую поверхность. Зная функцию f(x, y), можно найти интегральную функцию распределения, которая будет равна
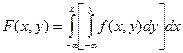 .
.
Дата добавления: 2016-04-19; просмотров: 676;
