Условные законы распределения случайных величин
Ранее были получены формулы для нахождения плотностей распределения составляющих величин 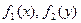 по плотности распределения системы двух случайных величин f(x, y).
по плотности распределения системы двух случайных величин f(x, y).
В ряде случаев бывает необходимо определять плотность распределения системы двух случайных величин f(x, y) по известным плотностям распределения отдельных случайных величин 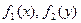 , входящих в систему.
, входящих в систему.
Для решения этой задачи кроме плотностей распределения отдельных случайных величин 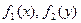 необходимо знать их взаимные связи и зависимость между ними. Эта зависимость характеризуется условными законами распределения, которые являются аналогами условных вероятностей.
необходимо знать их взаимные связи и зависимость между ними. Эта зависимость характеризуется условными законами распределения, которые являются аналогами условных вероятностей.
Условным законом распределения случайной величины X, входящей в систему (X, Y) называют ее закон распределения, вычисленный при условии, что другая случайная величина Y приняла определенное значение y.
Условные функции распределения случайных величин X и Y будем обозначать через F(x/y) и F(y/x) соответственно, а условные плотности распределения – через f(x/y) и F(y/x).
Постановка задачи. Пусть имеется система случайных величин (X, Y), причем известна ее плотность распределения f(x, y). Требуется найти условную плотность распределения f(x/y) случайной величины X при условии, что случайная величина Y приняла определенное значение y.
Для решения задачи рассмотрим элементарный прямоугольник со сторонами d x, d y (рис. 3.8).
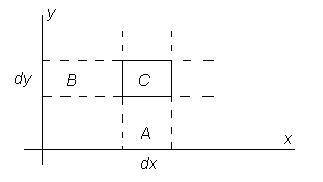
Рисунок 3.8 Элементарный прямоугольник со сторонами d x, d y
Обозначим через C – событие попадания случайной точки в прямоугольник C, через A -событие попадания случайной точки в полосу A, а через B - событие попадания случайной точки в полосу B.
Так как событие C является произведением событий A и B, поскольку может произойти только при появлении и события A и события B, то вероятность события C можно определить с помощью теоремы произведения зависимых событий, т.е.
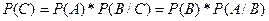 .
.
Откуда 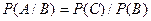 , но
, но 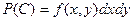 и
и 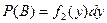 .
.
Тогда 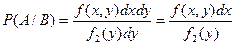 . Разделив обе части этого равенства на
. Разделив обе части этого равенства на 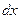 , получим
, получим 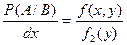 . В этом выражении отношение
. В этом выражении отношение 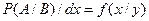 , так как оно представляет собой количество условной вероятности, приходящейся на единицу длины случайной величины X, т.е. является условной плотностью распределения случайной величины X, при условии, что случайная величина Y приняла определенное значение y.
, так как оно представляет собой количество условной вероятности, приходящейся на единицу длины случайной величины X, т.е. является условной плотностью распределения случайной величины X, при условии, что случайная величина Y приняла определенное значение y.
Следовательно,
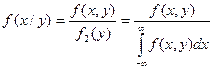 , а
, а 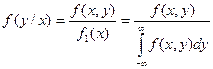 .
.
Пример 3. В условиях примера 1 определить условную плотность распределения f(x/y) случайной величины X.
Решение. Так как 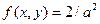 ,
, 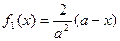 ,
, 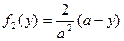 , то
, то
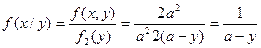 , т.е.
, т.е. 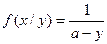 .
.
Если случайные величины дискретные, то вместо условных плотностей распределения определяются условные вероятности
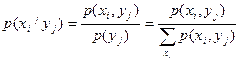 , а
, а 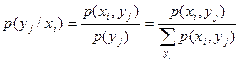 .
.
Дата добавления: 2016-04-19; просмотров: 928;
