Числовые характеристики СВ
О каждой СВ необходимо прежде всего знать ее некоторое среднее значение около которого группируются возможные значения СВ, а также какое-либо число, характеризующее степень разбросанности этих значений относительно среднего.
Рассмотрим дискретную СВ Х, имеющее возможные значения х1,х2,…,хn, с вероятностями р1,р2,…,рn.
Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех возможных значений СВ на вероятности этих значений:
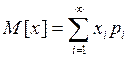
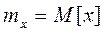 .
.
Математическим ожиданием непрерывной СВ Х, возможные значения которой принадлежат отрезку [a,b] называют определенный интеграл.
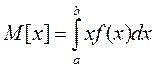 ,
,
если возможные значения непрерывной СВ Х принадлежат всей оси Ох, то математическое ожидание определяется интегралом:

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной, т.е. M[C]=C.
доказательство: постоянную величину, можно рассматривать как случайную величину, которая с вероятностью 1 принимает значение С.
M[C]=C*1=C.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания, т.е.
M[CX]=CM[X].
доказательство: для дискретной СВ 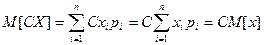 , для непрерывной СВ
, для непрерывной СВ  .
.
Модой М0 дискретной СВ называется ее наиболее вероятное значение, для непрерывной СВ мода есть такое значение СВ, при котором плотность распределения имеет максимум
f(M0)=max.
Если многоугольник распределения (кривая распределения)имеет два или несколько максимумов, то распределение называется двухмодульным или многомодульным.
Модульной М0 СВ Х называется, такое ее значение, относительно которого равновероятно получение большего или меньшего значения СВ, т.е
P(X<M0)= P(X>M0)
Геометрическая медиана – это абсцисса точки, в которой площадь, ограниченная кривая распределения делится пополам.
F(M0)=P (X<M0)=0,5.
Если распределение одномодульное и симметрическое, то все три характеристики mx, M0,Md – совпадают.
Основными характеристиками рассеивания СВ являются дисперсия и среднеквадратическое отклонение (СКО).
Дисперсией СВ называется МОЖ квадрата отклонения величины от ее МОЖ, т.е. D[x]=M[(x-mx)2]
Для дискретной СВ дисперсия выражается суммой 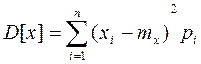 .
.
Для непрерывной СВ дисперсия выражается интегралом  .
.
Для большего удобства желательно иметь характеристику по размерности совпадающую с размерностью СВ. Такой характеристикой является среднеквадратическое отклонение, которое представляет собой положительный квадратный корень из ее дисперсии СКО Х обозначают dх .
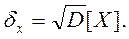
Свойство 1. Дисперсия постоянной величины равна нулю.
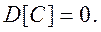
доказательство: т.к. 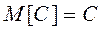 , то
, то 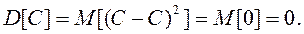
Свойство 2. Дисперсия произведения постоянной величины на СВ рана произведению квадрата постоянной величины на дисперсию СВ
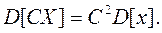
доказательство: 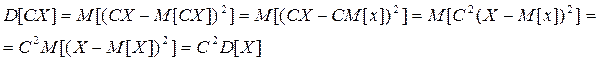
Свойство 3. Дисперсия СВ равна математическому ожиданию квадрата СВ минус квадрат ее МОЖ
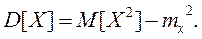
Доказательство: для дискретной СВ
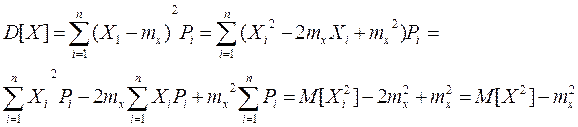
Дата добавления: 2016-03-05; просмотров: 1027;
