Функция распределения равна единице.

F(-∞) =0 F(+∞)=1

Из рассмотренных свойств следует, что график функции распределения для непрерывной СВ имеет следующий вид:

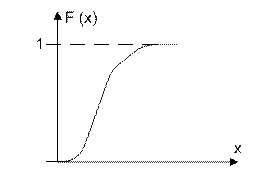
Функция распределения непрерывной СВ является ее исчерпывающей вероятностной характеристикой. Но она имеет недостаток, заключающийся в том, что по ней трудно судить о характере распределения СВ в небольшой окрестности той или другой точки на числовой оси. Более наглядное представление дается функцией, которая называется плотностью распределения вероятности или дифференциальным законом распределения СВ.

Предел отношения вероятности попадания непрерывной СВ на элементарный участок от Х до Х+ΔХ к длине этого участка ΔХ, когда ΔХ стремится к нулю, называется плотностью распределения случайной величины в точке Х и обозначается f(x).

Смысл плотности распределения f(x) состоит в том, что она указывает на то, как часто появляется случайная величина в точке Х в котором окрестности точки Х при проведении опытов

f(x)= 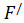(x).

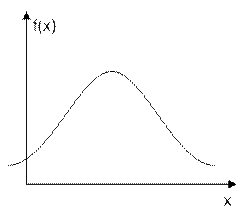
Кривая, изображающая плотность распределения f(x) СВ называется кривой распределения.

Дадим теперь более строго определение непрерывной СВ .